| |
為方便計我們以 R 代表所有實數的集合,R+ 表所有正實數及 0 的集合。以下所討論的函數,都是實函數,若不特別聲明其定義域 (domain of definition) 則自然指 R。
- 定義:
- 設 g(x) 為一定義在區間 (a,b) 上的函數,
若過於任何在 (a,b) 中的兩點 x,y,
下面不等式:
恆成立。如此的 g 稱為在 (a,b) 上的一凸函數。
我們要特別對此種函數的圖形作一觀察,也好使讀者明瞭為何稱滿足不等式(1)式者的函數為凸函數或上凹函數。如圖(1),我們將證明任何在

圖1
|
(a,b) 區間之三點 A(x),B(y) 及 C(z),設 x<z<y,
則 g(z) 之值必位於連結 D(x,g(x)),F(y,g(y)) 兩點之直線下方。
這個證明很簡單。由 A,B,C 作垂線分別交 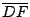 於 D,F,E,又由 D 作平行於 x 軸之直線交 於 D,F,E,又由 D 作平行於 x 軸之直線交 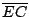 , ,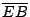 於 G 及 H。若令 於 G 及 H。若令
則 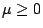 , ,
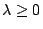 且 且
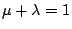 。又由此例知 。又由此例知
故
由(1)及
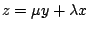 知 知
故直線 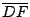 上的點高於點 (z,g(z));x<z<y。這個限制,使得 g 的圖形,自然非得向內凹陷,也就是所謂的凸(或上凹)函數名稱的由來。 上的點高於點 (z,g(z));x<z<y。這個限制,使得 g 的圖形,自然非得向內凹陷,也就是所謂的凸(或上凹)函數名稱的由來。
知道滿足條件(1)的函數為凸函數。但問題是有時我們無法利用它來判定某些函數是否為凸函數。
因(1)本身涉及的是任何兩個介於 (a,b) 中的點,我們也不可能逐一地檢驗。好在由於上面凸函數的幾何性質,
我們有時可以利用求一個函數的第二階導函數,來判定一個函數是否為凸函數?
假定 g(x) 在 (a,b) 上有定義且其第二階導函數 g''(x) 在 (a,b) 上到處存在
(注意:不見得每個函數的第二階導函數存在,但在一般所見到的函數,只要不是精工巧構的,總有第二階或更高階的導函數),
若  , ,
 ,則 g(x) 為 (a,b) 上的一凸函數,例如 ,則 g(x) 為 (a,b) 上的一凸函數,例如
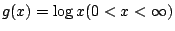 則 則
讀者不妨試描繪 g(x) 的圖形大要。
對於無微分觀念的讀者,我們提供下面一個凸函數的試驗法:設 g(x) 為定義在區間 (a,b) 上的一函數,且滿足
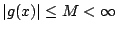 , ,
 ,(即 g 為有界的)若 g 在 (a,b) 上滿足: ,(即 g 為有界的)若 g 在 (a,b) 上滿足:
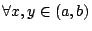 , ,
則 g 為 (a,b) 上的一凸函數。
這個證明涉及極限,連續等概念,讀者姑且信之,以後我們會用此條件,來檢驗某些函數是否為凸函數。
由於我們以後的討論,不僅限於一個變數,一般會在 n (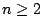 ) 度的實向量空間 Rn 或 ) 度的實向量空間 Rn 或
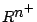 中。下面首先證明(1)式可以推廣到 n>2 的一般情形。 中。下面首先證明(1)式可以推廣到 n>2 的一般情形。
-
- 定理1:
- 設 g 為 (a,b) 上的一凸函數,
則
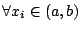 , (i=1,2,…,n); , (i=1,2,…,n);
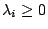 , (i=1,2,…,n), , (i=1,2,…,n),
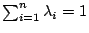 , ,
- 證:
- 用數學歸納法。很顯然(2)式對 n=1,2 時皆成立。
假設(2)式對 n=k-1 時成立,我們將證對 n=k 時(2)式亦成立。
令
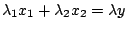 , ,
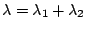 則由歸納法假設得知
則由歸納法假設得知
因為
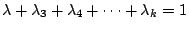 共 k-1 項,又 共 k-1 項,又
此式及上式得知(2)式對 n=k 亦成立。故由歸納法原理知(2)式恆成立。
我們現在舉些有關凸函數的應用。
-
- 定理2:(Arithematic-Geometric Mean Inequality)
- 設
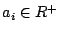 ,i=1,2,…,n,則 ,i=1,2,…,n,則
- 註:
- 這就是所謂的算術平均大於幾何平均。
- 證:
- 很明顯若 ai 中有一為 0 則不等式自然成立,故可設 ai>0
令
 , x>0 則依據圖形或考慮 , x>0 則依據圖形或考慮
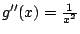 得知 g 在 得知 g 在 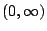 上為一凸函數。於是 上為一凸函數。於是
而
於是
現 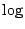 為正實數的遞增函數,所以由上式得 為正實數的遞增函數,所以由上式得
-
- 定理3 (Cauchy 不等式)
- 設 ai (i=1,2,…,n) 及 bi (i=1,2,…,n) 為兩組正實數,
則
- 證:
- 設 y=g(x)=x2,則易知 g 為一凸函數。令
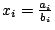 及 ti=bi2, 及 ti=bi2,
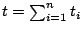 , ,
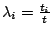 ,i=1,2,…,n
則由定理1可得 ,i=1,2,…,n
則由定理1可得
即
原式得證。
- 註:
- 原命題對所有的實數皆成立,在此為簡明計,假設所有的bi不為零,不然可把為0的bi代以
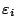 (充分小的參數)將結果取極限,仍可得原式。 (充分小的參數)將結果取極限,仍可得原式。
現在我們討論具有下列形式的不等式:
其中
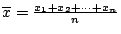 , x1,x2,…,xn 為實數。如果我們令 , x1,x2,…,xn 為實數。如果我們令
則前面的(3)式就可表成(4)的形式。由於(4)的特殊形式,
使得我們不妨考慮下面更廣泛的形式:
此時 y1,y2,…,yn 不一定要相等,但它們在某些意義上
(這是我們將要進一步討論的地方)比 x1,x2,…,xn 要來得緊湊些,
即沒有 x1,x2,…,xn 來得分散。我們主要問的就是
{xi}i=1n 及
{yi}i=1n 在何種條件下,對何種函數 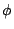 ,(5)式總成立? ,(5)式總成立?
|
|
|