| |
最後我們來討論有關含有兩變數動差的不等式。設為 (X,Y) 為連續型機率變數而其機率密度函數為 h(x,y),則
就分別成 X,Y 的機率密度函數。又
分別稱做 X,Y 的平均,變異數,X,Y 的共變差。
對於這些我們亦可證出下列不等式
更一般化的不等式是,對於任意的機率變數 X,Y 間所成的 Hölder 不等式
但 r,s 滿足
若在不等式(5)中的 X,Y 以 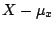 , , 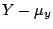 代替,而 r=s=2,則(5)就成為不等式(4)。
為了證明不等式(5),首先我們來證明 代替,而 r=s=2,則(5)就成為不等式(4)。
為了證明不等式(5),首先我們來證明
(但 r,s 滿足(6)式)
設函數
則由其微分可知,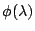 在 在 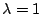 時取最小值 0。因此可導出不等式 時取最小值 0。因此可導出不等式
再令
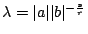 ,則 ,則
兩邊再乘以 |b|s,則由
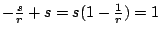 ,可得不等式(7)的結果。 ,可得不等式(7)的結果。
然後在不等式(7)中,令
則
兩邊再取其期望值,則可得
於是我們得到了不等式(5)的證明。
用同樣方法又可以證明 Minkowski 不等式
當我們討論二變數的機率變數 (X,Y) 時,將其共變差標準化所得的值
具有很重要的地位。我們稱這值為 X 與 Y 的相關係數,由不等式(4)可知,不等式
成立。當  (或 -1)時,(X,Y) 的分佈集積在具有正(或負)的斜率的直線上,因此 (或 -1)時,(X,Y) 的分佈集積在具有正(或負)的斜率的直線上,因此  (或 (或 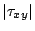 )被認為是衡量二維分佈的直線傾向的值。
又 )被認為是衡量二維分佈的直線傾向的值。
又 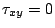 時, 時, ,這時 X,Y 可能是互相獨立。
換句話說,若 X,Y 互為獨立時, ,這時 X,Y 可能是互相獨立。
換句話說,若 X,Y 互為獨立時, ,但其逆就不一定成立。 ,但其逆就不一定成立。
|
|
|