生成函數與差分方程

．原載於數學傳播第二卷第四期
．作者當時任教於清華大學數學系

生成函數與差分方程

夏宗匯

組合數學是一門有廣泛應用且頗引人入勝的數學分枝。研讀組合數學並不需要太多數學背景;在高中數學裏便已介紹了許多有趣且困難的排列組合問題。但在那裏所用的方法卻是初等的；有如解算術題，每一問題有各自思考方法與技巧。在本文中我們將討論一類排列組合問題，它們可以用列線性回歸方程 (linear recurrence) 的方法來求解，並用例題來說明兩種回歸方程求解的步驟。我們所作僅為一粗淺介紹，所選取的材料可為讀過微積分的讀者所接受。有興趣的讀者應進一步參閱本文後所列參考資料。

我們先用例題來說明回歸方程的數學意義和它與排列組合問題之關係。

[例1] 設有 n 個半徑遞增的圓環依大小套在一圓柱上，最大的環在最下面。我們要將這些環移置至另一圓柱上，另有第三個圓柱作暫時放置圓環用，但移置時規定大環永不可放在小環上面，每次移動一個環，問最少要移動幾次才可將 n 個環由一圓柱移至另一圓柱？這便是著名的「河內之塔」問題 (The tower of Hanoi problem)。顯見當 n=1 時，我們只需 1步；當 n=2 時，我們需要 3 步。但當 n 很大時，例如， n=64，問題的答案便不顯然了。設 a_n (n=1,2,3,…) 為移動 n 個環的最少次數，則 a₁=1, a₂=3。如果 n>2，我們可先用 a_n-1 步將第一柱上面之 n-1 個環移至第三柱上，然後將最大環移至第二柱，最後再用 a_n-1 步將第三柱上之 n-1 個環放在第二柱最大環之上面。這樣便完成以最少步數移置這 n 個環，故得

a_n	=	$\displaystyle 2a_{n-1}+1 \; , \quad (n \geq 2)$	(1)
a₁	=	1	(2)

數列 $\{ a_n \}_{n=1}^\infty$ 可看成是定義在正整數集上的函數。 (1)式表示了兩相連正整數間該函數值之關係，稱為回歸方程，又稱差分方程 (difference equation)。 (2)式稱為方程(1)之邊界條件 (boundary condition)。如所給 n 之值不大，我們可用邊界條件 (2)代入 (1)式之右邊而逐步得出 a_n之值。方程 (1)之解是一用 n 表達 a_n 的一般形式。我們先討論應用生成函數 (generating function) 的方法求滿足邊界條件(2)之方程 (1)的解。

我們先提出生成函數的定義。設 $\{ a_n \}_{n=0}^\infty$ $= \{ a_0,a_1,\cdots,a_n,\cdots \}$ 是一數列，則函數

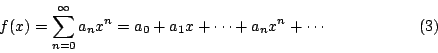
$\begin{displaymath} f(x)=\sum_{n=0}^\infty a_nx^n=a_0+a_1x+\cdots +a_nx^n+\cdots \eqno{(3)} \end{displaymath}$

稱為與數列 $\{ a_n \}_{n=0}^\infty$ 對應之生成函數。生成函數又稱形式冪級數 (formal power series)，是看成一代數對象，我們無需顧慮其收斂性。生成函數可以相加與相乘，也可以形式地求其導數與反導數這些運算法則恰如冪級數的對應運算。設

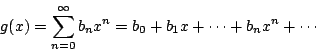
$\begin{displaymath}g(x)=\sum_{n=0}^\infty b_nx^n=b_0+b_1x+\cdots +b_nx^n+\cdots \end{displaymath}$

是與數列 $\{ b_n \}_{n=0}^\infty$ 所對應之生成函數，則生成函數的相加與相乘是定義為

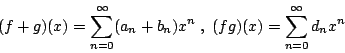
$\begin{displaymath} (f+g)(x)=\sum_{n=0}^\infty (a_n+b_n)x^n \; , \; (fg)(x)=\sum_{n=0}^\infty d_nx^n \end{displaymath}$

其中

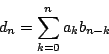
$\begin{displaymath} d_n=\sum_{k=0}^{n} a_kb_{n-k} \end{displaymath}$

生成函數 f(x) 之導數是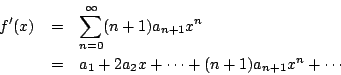

$\begin{eqnarray*} f'(x)&=&\sum_{n=0}^\infty (n+1)a_{n+1}x^n\\ &=&a_1+2a_2x+\cdots +(n+1)a_{n+1}x^n+\cdots \end{eqnarray*}$

本文所考慮的生成函數均為整係數。如果由(3)給出之生成函數 f(x) 是整係數的且首項係數 a₀ 為 1，則 f(x) 還可以除另一整係數的生成函數，所得之商仍為一整係數生成函數。兩個生成函數相等僅當它們對應之係數均相等。我們將在例題中用實際計算來說明這些運算，不再在理論上作詳細說明，其理論基礎請參閱參考資料[3]。有關生成函數在組合數學中之其它應用可參閱[2,4]。

回到回歸方程(1)，顯見可令 a₀=0而仍保持由式(1)及(2)所建立之關係。將滿足(1)與 (2)之各數用數列 $\{ a_n \}_{n=0}^\infty$ 記出，並設 g(x) 為與之對應的生成函數，則我們有

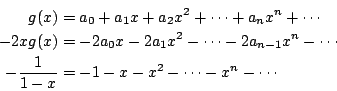
$\begin{eqnarray*} g(x) &=& a_0 + a_1x + a_2x^2 + \cdots + a_nx^n + \cdots \\ -2... ...ots \\ -\frac{1}{1-x} &=& -1 - x - x^2 - \cdots - x^n - \cdots \end{eqnarray*}$

如將上面三個生成函數相加，則由式(1)及 a₀ 之定義可知所得之生成函數的係數由第二項起均為零；g(x) 下面的二生成函數便是依據此一原則所定出。故得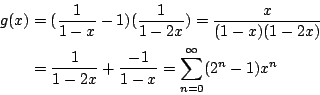

$\begin{displaymath}g(x)-2xg(x)-\frac{1}{1-x} =-1\end{displaymath}$

解出 g(x) 有

$\begin{eqnarray*} g(x)&=&(\frac{1}{1-x} -1)(\frac{1}{1-2x}) =\frac{x}{(1-x)(1-2x... ... &=&\frac{1}{1-2x} +\frac{-1}{1-x} =\sum_{n=0}^\infty (2^n-1)x^n \end{eqnarray*}$

因得滿足邊界條件(2)之方程(1)的解為

$\begin{displaymath} a_n=2^n-1 \,\, (n \geq 1) \end{displaymath}$

當 n=64 時，移動 64 個環的最小步數 a_n=2⁶⁴-1 是個很大數字。

[例2] 在平面上畫 n 個橢圓，每兩個必恰好交於兩點，但每三個又不能交於同一點，問這些橢圓將平面分隔成多少區域?

設 a_n (n=1，2，…)為 n 個橢圓將平面分隔之區域個數，則顯見 a₁=2, a₂=4。當 $n \geq 5$ 時，用觀察法求 a_n 便有困難了。設在平面上有 n-1 個橢圓，將平面份為 a_n-1 個區域，如再在平面上畫入第 n 個橢圓，則它與原有 n-1 個橢圓中每一個均恰交於兩點。這 2(n-1) 個交點將第 n 個橢圓分成 2(n-1) 個弧段，而每一弧段又將所在的 2(n-1) 個原有區域一分為二，故得回歸方程

$\begin{displaymath}\left\{ \begin{array}{rcl} a_n & = & a_{n-1}+2(n-1)\, , (n \geq 2) \\ a_1 & = & 2 \end{array}\right. \eqno{(4)} \end{displaymath}$

定義 a₀=2 並設 g(x) 為數列 $\{ a_n \}_{n=0}^\infty$ 之生成函數，則

$\begin{displaymath} \begin{array}{rllllll} g(x)&=a_0&+a_1x&+a_2x^2&+\cdots &+a_n... ...(1-x)^2}&= & &-2x^2&-\cdots &-2(n-1)x^n&-\cdots \\ \end{array}\end{displaymath}$

其中，上面第三個等式可由下法導出: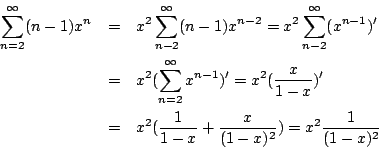

$\begin{eqnarray*} \sum_{n=2}^\infty (n-1)x^n&=&x^2\sum_{n-2}^\infty (n-1)x^{n-2}... ...&x^2(\frac{1}{1-x} +\frac{x}{(1-x)^2} )=x^2\frac{1}{(1-x)^2} \\ \end{eqnarray*}$

將上三式相加得

$\begin{displaymath}g(x)-xg(x)-\frac{2x^2}{(1-x)^2} =2\end{displaymath}$

即

$\begin{displaymath} g(x)=\frac{1}{1-x} (2+\frac{2x^2}{(1-x)^2}) = \frac{1}{(1-x)^3} (2-4x+4x^2) \end{displaymath}$

因為

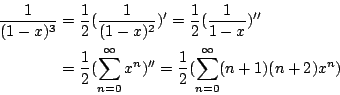
$\begin{eqnarray*} \frac{1}{(1-x)^3}&=&\frac{1}{2} (\frac{1}{(1-x)^2})'=\frac{1}{... ...n=0}^\infty x^n)''=\frac{1}{2} (\sum_{n=0}^\infty (n+1)(n+2)x^n) \end{eqnarray*}$

故

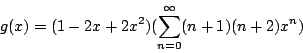
$\begin{displaymath} g(x)=(1-2x+2x^2)(\sum_{n=0}^\infty (n+1)(n+2)x^n) \end{displaymath}$

最後得回歸方程(4)之解為

$\begin{eqnarray*} a_n&=&(n+1)(n+2)-2n(n+1)+2(n-1)n \\ &=&n^2-n+2 \end{eqnarray*}$

[例 3] 問在用整數 0 與 1 組成的 n 位數中，有多少不含兩個相連的 0?

顯見有 2 個一位數；3 個二位數：01,10 與 11。設 a_n 為由 0 與 1 所組成不含兩個相連的 0 之 n-1 位數之個數（其中 n 錯開一位是由於歷史上原因），則得回歸方程

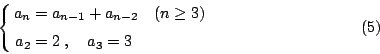
$\begin{displaymath} \left\{ \begin{eqalign} a_n &= a_{n-1}+a_{n-2} \quad (n \ge... ...\\ a_2 &= 2 \; , \quad a_3=3 \end{eqalign}\right. \eqno{(5)} \end{displaymath}$

這是因為在不含兩個相連的零之由 0 與 1 組成 n-1 位數中，最後一位數如是零，則最後第二位數就不能是零，這樣的數一共有 a_n-2 個；最後一位數如是 1，則前面 n-2 個數可任意選取 0 或 1，只要兩個零不相連便可，這樣的數一共有 a_n-1 個。式(5)給出三個相連的 a_n 之值關係，稱為 2 階回歸方程，需要 2 個邊界條件。由(5)我們可定義 a₁=1, a₀=1。依前法，令 g(x) 是數列 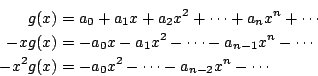$\{ a_n \}_{n=0}^\infty$ 之生成函數，則得

$\begin{eqnarray*} g(x) &=& a_0 + a_1x + a_2x^2 + \cdots + a_nx^n + \cdots \\ -x... ... \cdots \\ -x^2g(x) &=& -a_0x^2 - \cdots - a_{n-2}x^n - \cdots \end{eqnarray*}$

故得

g(x)(1-x-x²) = 1

利用部分分式得

$\begin{displaymath} g(x)=\frac{1}{1-x-x^2} =\frac{1+\sqrt{5}}{2\sqrt{5}} (\frac{... ...-\alpha x})-\frac{1-\sqrt{5}}{2\sqrt{5}} (\frac{1}{1-\beta x}) \end{displaymath}$

其中

$\begin{displaymath}\alpha =\frac{1+\sqrt{5}}{2} \, ,\,\beta =\frac{1-\sqrt{5}}{2}\end{displaymath}$

故得回歸方程(5)之解是

$\begin{eqnarray*} a_n&=&\frac{1+\sqrt{5}}{2\sqrt{5}} (\frac{1+\sqrt{5}}{2})^n -\... ...t{5}}((\frac{1+\sqrt{5}}{2})^{n+1}-(\frac{1-\sqrt{5}}{2})^{n+1}) \end{eqnarray*}$

實際上數列 $\{ a_n \}_{n=0}^\infty$ 的前幾項可很容易得出，由式 (5)知 a₀=1， a₁=1起後面每一項均等於其前面兩項之和，故該數列的前幾項是

$\begin{displaymath}1,\, 1,\, 2,\, 3,\, 5,\, 8,\, 13,\, 21,\, 34,\cdots\end{displaymath}$

這些數稱為 Fibonacci數，它們背後藏有一段歷史悠久且頗具趣味的數學故事。但這些已不在本文範圍內了。

前面我們提出了幾個簡單的回歸方程的例子，並說明用生成函數求解的過程。在下面我們將回歸方程看成是一種差分方程，並介紹另一種方程求解的方法。我們已提過一個數列 a= $\{ a_n \}_{n=0}^\infty$ 可看成是定義在非負整數集上的函數，其於整數 $n\geq 0$ 之值就是 a_n。差分算子 Δ(difference operator)是一在這些函數組成的集合上之變換，其定義為

$\begin{displaymath} \Delta a_n=a_{n+1}-a_n \end{displaymath}$

高階差分算子 $\Delta^k$ (k=2,3,…)是定義為

$\begin{displaymath} \Delta^ka_n=\Delta(\Delta^{k-1}a_n) \end{displaymath}$

我們並定義 $\Delta^{0}=I$ ，其中 I 是恆等算子，即 Ia_n=a_n (n=0,1,2,…)。與差分算子有密切關係的是位移算子 E (Translation operator)，其定義為

Ea_n=a_n+1

高階位移算子 E^k (k=2,3,…) 是定義為

E^ka_n=E(E^k-1a_n)=a_n+k

我們並定義 E⁰=I，顯見有 $E=\Delta +I$ 。任何方程含有差分算子或與其等價之位移算子的稱為差分方程 (difference equation)。一個 k階常係數線性差分方程 (或回歸方程)有一般形式

$\begin{displaymath} C_0a_{n+k}+C_1a_{n+k-1}+\cdots +C_ka_n=b_n \, ,\eqno{(6)} \end{displaymath}$

其中 $\{ b_n \}_{n=0}^\infty$ 是一給定數列，C₀, C₁, …, C_k 是給定之常數。如果有 k 個相連的值為給出，稱為邊界條件，則方程(6)有唯一的解。與 (6)對應之齊次差分方程是

$\begin{displaymath} C_0a_{n+k}+C_1a_{n+k-1}+\cdots +C_ka_n=0 \, , \eqno{(7)} \end{displaymath}$

前述之方程 (1)與 (4)均是一階非齊次差分方程;方程 (5)是二階齊次差分方程。利用位移算子，方程 (6)與 (7)又可記為

$\begin{displaymath} (C_0E^k+C_1E^{k-1}+\cdots +C_{k-1}E+C_kI)a_n=b_n \eqno{(8)} \end{displaymath}$

及

$\begin{displaymath} (C_0E^k+C_1E^{k-1}+\cdots +C_{k-1}E+C_kI)a_n=0 \ , \eqno{(9)} \end{displaymath}$

方程 (9)之解稱為齊次解；任意滿足方程 (8) 之解稱特別解。讀者已可觀察到 k階常係數線性差分方程與微積分中的 k 階常係數線性微分方程之間相似性；實際上它們之間有許多相平行的性質。例如所有齊次解形成的集合是一向量空間；方程(8)之解必為一個齊次解及某個特別解之和。這些性質的證明與微分方程中相應性質的證明相似，我們不在此詳細說明。有關差分方程一般性質請參閱參考資料[1]。

下面我們討論 k階齊次常係數線性差分方程 (9)之求解步驟。在 (9)中令 a_n=rⁿ，我們有

$\begin{displaymath} (C_0r^k+C_1r^{k-1}+\cdots +C_{k-1}r+C_k)r^n=0 \end{displaymath}$

我們不考慮 r=0的情況，故又有

$\begin{displaymath} C_0r^k+C_1r^{k-1}+\cdots +C_{k-1}r+C_k=0 \eqno{(10)} \end{displaymath}$

方程 (10)是一次代數方程式，稱為與 (9)對應之特徵方程式;它有 k個根，稱為方程 (9)之特徵根。如果 (10)有 k個不同的根 r₁， r₂， …， r_k，則任一方程 (9)之解有形式

$\begin{displaymath} a_n=A_1r_1^n+A_2r_2^n+\cdots +A_kr_k^n \end{displaymath}$

其中 A₁, A₂, …, A_k 是未定係數，由所給出的邊界條件所決定。如果一特徵根 r是 (10)之 m 重根，則與之對應的齊次解是

$\begin{displaymath} (A_0+A_1n+\cdots +A_{m-1}n^{m-1})r^n \end{displaymath}$

如果方程 (10)有一對共軛複根 p+qi 及 p-qi，則與之對應之齊次解又可寫成

$\begin{displaymath} A_1(p+qi)^n+A_2(p-qi)^n = \rho^n(B_1\cos n\theta +B_2\sin n\theta) \end{displaymath}$

其中 $\rho=\sqrt{p^2+q^2}$ ， $\theta=\tan^{-1}(q/p)$ ，B₁=A₁+A₂ 及 B₂=i(A₁-A₂)。下面我們在用例題來說明齊次差分方程之求解步驟。

[例4]
解例3中的齊次差分方程 (5):

$\begin{displaymath}\left\{ \begin{array}{l} a_{n+2}-a_{n+1}-a_n=0 \\ a_0=1\,\mbox{,}\, a_1=1 \\ \end{array}\right. \eqno{(11)} \end{displaymath}$

方程 (11)之特徵方程是

r²-r-1=0

它有兩個不同的特徵根 $(1+\sqrt{5})/2$ 與 $(1-\sqrt{5})/2$ ，故其齊次解有形式

$\begin{displaymath} a_n=A_1(\frac{1+\sqrt{5}}{2})^n+A_2(\frac{1-\sqrt{5}}{2})^n \eqno{(12)} \end{displaymath}$

為了決定未定係數 A₁ 與 A₂，我們將(11)中之邊界條件代入(12)得

$\begin{displaymath}\left\{ \begin{array}{rcl} 1&=&A_1+A_2 \\ 1&=&A_1(\frac{1+\s... ...)+A_2(\frac{1-\sqrt{5}}{2}) \\ \end{array}\right. \eqno{(13)} \end{displaymath}$

解聯立方程 (13)得

$\begin{displaymath} A_1=\frac{1+\sqrt{5}}{2\sqrt{5}}\,\mbox{,}\, A_2=-\frac{1-\sqrt{5}}{2\sqrt{5}} \end{displaymath}$

因此方程 (11)之解是

$\begin{eqnarray*} a_n&=&\frac{1+\sqrt{5}}{2\sqrt{5}} (\frac{1+\sqrt{5}}{2})^n -\... ...t{5}}((\frac{1+\sqrt{5}}{2})^{n+1}-(\frac{1-\sqrt{5}}{2})^{n+1}) \end{eqnarray*}$

[例5] 計算 n 階行列式

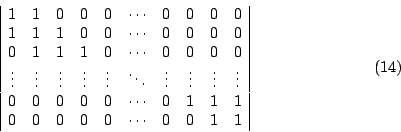
$\begin{displaymath} \begin{array}{\vert cccccccccc\vert} 1&1&0&0&0&\cdots&0&0&0&... ...&1&1&1 \\ 0&0&0&0&0&\cdots&0&0&1&1 \\ \end{array}\eqno{(14)} \end{displaymath}$

設 (14)中之 n階行列式之值為 a_n，由第一列將 (14)展開得差分方程

$\begin{displaymath}\left\{ \begin{array}{l} a_n=a_{n-1}-a_{n-2} \\ a_1=1\,\mbox{,}\, a_2=0 \\ \end{array}\right.\eqno{(15)} \end{displaymath}$

它的特徵方程是 r²-r+1=0，故有兩個共軛複根

$\begin{displaymath} r_1=\frac{1}{2} +i\frac{\sqrt{3}}{2} = \cos\frac{\pi}{3} +i\sin\frac{\pi}{3} \; , \end{displaymath}$

$\begin{displaymath} r_2=\frac{1}{2} -i\frac{\sqrt{3}}{2} =\cos\frac{\pi}{3} -i\sin\frac{\pi}{3} \end{displaymath}$

得方程 (15)之齊次解有形式

$\begin{displaymath}a_n=B_1\cos\frac{n\pi}{3} +B_2\sin\frac{n\pi}{3}\eqno{(16)}\end{displaymath}$

將 (15)中之邊界條件代入 (16)有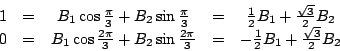

$\begin{displaymath} \begin{array}{ccccc} 1&=&B_1\cos\frac{\pi}{3} +B_2\sin\frac{... ...2\pi}{3} &=&-\frac{1}{2} B_1+\frac{\sqrt{3}}{2} B_2 \end{array}\end{displaymath}$

從而得未定係數 B₁=1， $B_2=\frac{1}{\sqrt{3}}$ 。方程(15)之解是

$\begin{displaymath} a_n=\cos\frac{n\pi}{3} +\frac{1}{\sqrt{3}}\sin\frac{n\pi}{3} \end{displaymath}$

由方程 (15)可見由 n=1起 a_n之值的首幾項是

$\begin{displaymath}1\, ,\, 0\, ,\, -1\, ,\, -1\, ,\, 0\, ,\, 1\, ,\, 1\, ,\, 0\, ,\cdots\end{displaymath}$

最後我們介紹一種非齊次差分方程 (8)的求解步驟。由上面討論知只需求出方程 (8)的某個特別解。我們所用的是一種經驗法，是由方程 (8)之右邊 b_n之形式來判斷特別解可能有的形式，然後再決定其中未定係數。下表列出幾種常遇到的 b_n形式

$\begin{displaymath} \begin{array}{c\vert c} b_n & \mbox{{\fontfamily{cwM2}\fonts... ...\cos a_n & B_1\sin a_n +B_2\cos a_n \\ \end{array}\eqno{(17)} \end{displaymath}$

其中表之右列中 B,B₁,B₂,…,B_p 為未定係數。這種解法也是求常微分方程之非齊次解時常用方法之一，讀者應對這兩種情況之異同作一比較。

[例6] 問在由 0,1,2,3 所組成的 n 位數中有多少含有偶數個零？

設 a_n 是由 0,1,2,3 所組成的 n 位數中含偶數個 0 的個數，則在這些數中，最後一位數或者不為零，這樣的數有 3a_n-1 個；或者最後一位數為零，則它前面 n-1位中必有奇數個零，這樣的數一共有 4^n-1-a_n-1 個，故得 a_n=3a_n-1+4^n-1-a_n-1。顯然有 a₁=3，故所求的差分方程可寫成

$\begin{displaymath}\left\{ \begin{array}{rcl} a_{n+1}-2a_n&=&4^n \\ a_1&=&3 \end{array}\right.\eqno{(18)} \end{displaymath}$

方程 (18)之特徵方程式 r-2=0，它有唯一的特徵根 r=2，故得方程(18)之齊次解有形式

a_n=A2ⁿ

其中 A 是未定係數。為了求方程的特別解，由表(17)得它有形式 a_n=B4ⁿ，其中 B為未定係數。代入方程(18)得

B4ⁿ⁺¹-2B4ⁿ=4ⁿ

從而 $B=\frac{1}{2}$ 。因此方程(18)之任一解均有形式

$\begin{displaymath} a_n=A2^n+\frac{1}{2} 4^n \eqno{(19)} \end{displaymath}$

將(18)中邊界條件代入(19)得 $A=\frac{1}{2}$ ，因此方程(18)之解為

$\begin{displaymath} a_n=\frac{1}{2} (4^n-2^n) \end{displaymath}$

用試驗解法求特別解也有失效的情況，那時我們必需作必要的修正。最後我們舉下例來說明此點。

[例7] 解差分方程

$\begin{displaymath}\left\{ \begin{array}{rcl} a_{n+1}-a_n&=&2n \\ a_0&=&2 \\ \end{array}\right.\eqno{(20)} \end{displaymath}$

方程 (20)的特徵方程是 r-1=0，故它有唯一的特徵根 r=1。因此方程(20)的齊次解是 a_n=A(1)ⁿ=A，其中 A 是未定係數。根據表(17)方程(20)的特別解有形式

$\begin{displaymath} a_n=B_1+B_2n \eqno{(21)} \end{displaymath}$

但齊次解與特別解中均有一項是常數，將 (21)代入 (20)將無法決定未定係數 B₁。這時我們可以將特別解乘一最低次數之 n 的整數冪，使得齊次解與特別解中的這種相似項消失。因此我們可令方程(20)之特別解有形式 a_n=B₁n+B₂n² 並代入(20)得

B₁(n+1)+B₂(n+1)²-B₁n-B₂n² = 2n

比較兩邊係數得 B₁=-1, B₂=1。方程(20)之任一解均有形式

$\begin{displaymath}a_n=n^2-n+A \eqno{(22)}\end{displaymath}$

將(20)中之邊界條件代入(21)得 A=2，因此方程(20)之解為

a_n=n²-n+2

: 1. Levy, H. & F. Lessman, 《Finite Difference Equation》, Macmillian, 1961.
: 2. Liu, C. L., 《Introduction to Combinatorial Mathematics》, McGraw-Hill, 1968.
: 3. Niven, I., 《Formal power series, Amer. Math. Monthly》, 76(1969),871-889.
: 4.夏宗匯：〈組合數學中的生成函數〉《數學傳播》（第一卷第三期），六十五年十二月，51-58.

對外搜尋關鍵字：
．差分方程
．生成函數
．Fibonacci
．微分方程
．組合學
．費氏數列


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：陳文是

最後修改日期：4/26/2002