勒襄特的證明,其目的在探究,是否可以運用某他公理將平行公設演繹出來。但是對於平行公設的真實性,亦即,平行公設是否與真實空間的性質相符合,勒襄特是沒有任何懷疑的。在十九世紀的最初二十年中,偉大的德國數學家高斯(Gauss, 1777∼1855),最先持有這個具有「革命性的」觀念;在他看來,平行公設的真實性的問題,具有自然科學上的意義,換言之,它涉及真實的點與直線,如像在大地測量所應用的點與直線,是否遵循平行公設的問題。
我們知道,平行公設的陳述涉及直線的全長,亦即涉及其兩端在想像中無限延伸的整條直線;因為,說兩條直線是平行的,意思就是說,無論將它們延長多遠,它們永不相交。可是我們實驗所能觀察到的範圍,無論如何大,總是有限的,因此平行公設本身不可能藉實驗來證明。不過,我們已經談到過,平行公設與內角和定理在邏輯上是等值的陳述,而後者是可以在有限範圈內實施驗證的。所以,我們只要測量任何一個三角形的各角之和,如果是 180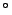 ,那末平行公設就成立了。當然,這個說法還不夠謹嚴,我們應該先證明「如果至少有一個三角形存在,其各角之和為 180 ,那末平行公設就成立了。當然,這個說法還不夠謹嚴,我們應該先證明「如果至少有一個三角形存在,其各角之和為 180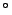 ,那末任何其他三角形的各角之和亦為 180 ,那末任何其他三角形的各角之和亦為 180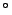 」;這是很容易證明的,但為節省篇幅,所以在此略去了。 」;這是很容易證明的,但為節省篇幅,所以在此略去了。
高斯曾經在哥廷根大學的附近,以三座山峰為頂點,測繪一個三角形,其各邊之長大約為三十哩。他以最大的精密度來測其各角。所得各角之和與 180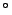 的歧離,似乎是在測量所不可避免的誤差範圍以內;因而,是否這個和是精確的 180 的歧離,似乎是在測量所不可避免的誤差範圍以內;因而,是否這個和是精確的 180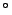 ,或是它與 180 ,或是它與 180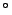 之間的差較測量所不可避免的誤差更小,這個問題仍待解決。 之間的差較測量所不可避免的誤差更小,這個問題仍待解決。
其實,這個企圖的失敗是可以事先預見的。為說明這一點,我們將三角形各角之和與 180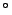 之間的差稱為該三角形的「角差」(defect)。然後我們將一個三角形 ABC 分為三角形 ABD 和 BCD,如圖四。於是我們有 之間的差稱為該三角形的「角差」(defect)。然後我們將一個三角形 ABC 分為三角形 ABD 和 BCD,如圖四。於是我們有
將以上兩式加起來,我們得
但是
 , ,
 ,所以我們得 ,所以我們得

圖四
|
於是我們得到一個定理:「三角形的角差是等於組成該三角形之諸分三角形的角差之和。」
現在讓我們想像,一個以太陽,地球和火星為頂點的三角形,其角差為 1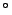 ,亦即其各角之和為 179 ,亦即其各角之和為 179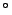 。然後我們將這個三角形劃分成與高斯所測繪的三角形差不多大小的許多三角形。太陽,地球和火星間的距離到達幾萬萬哩,故我們可以很容易的計算出來,其成分三角形將要超過一萬萬萬個。於是一個邊長三十哩的分三角形,其角差差不多只等於一度的一萬萬萬分之一。顯然,今天還沒有任何儀器能夠檢驗出這樣細微的角。這個以角差定理為基礎的計算,使我們不得不相信,當在地球上測量三角形時,將不可能遇到任何顯著的角差。在地球上,三角形的角差質際上是零,故三角形各角之和是180 。然後我們將這個三角形劃分成與高斯所測繪的三角形差不多大小的許多三角形。太陽,地球和火星間的距離到達幾萬萬哩,故我們可以很容易的計算出來,其成分三角形將要超過一萬萬萬個。於是一個邊長三十哩的分三角形,其角差差不多只等於一度的一萬萬萬分之一。顯然,今天還沒有任何儀器能夠檢驗出這樣細微的角。這個以角差定理為基礎的計算,使我們不得不相信,當在地球上測量三角形時,將不可能遇到任何顯著的角差。在地球上,三角形的角差質際上是零,故三角形各角之和是180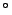 ;換言之,歐幾里得的平行公設及由其演繹出來的一切結論,在地球上均能成立。為人類所正確知道的最大三角形,是那些用來決定恆星視差 (parallaxes of fixed stars) 的三角形。 ;換言之,歐幾里得的平行公設及由其演繹出來的一切結論,在地球上均能成立。為人類所正確知道的最大三角形,是那些用來決定恆星視差 (parallaxes of fixed stars) 的三角形。
命 G 表一恆星,A 和 B 表地球在其繞日軌道中兩個相對的位置(如圖五)。線段 AB 為地球軌道的直徑,其長約 186 百萬哩。角 GAB 與 GBA 均可測得,因其頂點均在地球上。當然,我們可以選擇 A 與 B,以使 AB 垂直於 GM,則上述兩角相等。
 這個量,亦即 這個量,亦即
 ,稱為恆星G的「視差」。 ,稱為恆星G的「視差」。

圖五
|
如果直角三角形 GAM 的各角之和是 180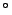 ,則恆星 G 的視差將是 ,則恆星 G 的視差將是  ,亦即地球軌道的半徑 AM 對恆星 G 所張的角。如果三角形 AGM 的各角之和小於180 ,亦即地球軌道的半徑 AM 對恆星 G 所張的角。如果三角形 AGM 的各角之和小於180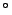 ,則恆星的視差將不是等於而是大於角 AGM。 ,則恆星的視差將不是等於而是大於角 AGM。
三角形 AGM 的角差是
 ,它顯然較視差 ,它顯然較視差
 為小。於是我們可以估計 為小。於是我們可以估計
天狼星 (Sirius)的視差已測得為0.38",織女星(Vergo)為0.08"。其對應的角差較視差為小,可見也是非常微小。測量視差所用的三角形是非常狹的,故僅有那些較遠的大三角形才可能有較大的角差,就天狼星而言,邊長AG約為AM之長的五十萬倍。這樣的情形,即使未來人類實現了太空旅行,能到達火星或海王星,也不可能有什麼改變。因為就整個太陽系的直徑而言,其與恆星間的距離比較起來,仍然是太小。
因此,歐幾里德的平行公設是否在整個空間中均能成立的問題,仍未能經由對角的直接測量而解決。不過,我們必須在心裏記住,雖然根據地球甚或太陽而測得的三角形,其各角之和是非常精確的等於 180 ,但是在以「宇宙的」大小為準的三角形中,其各角之和就可能不等於這個數字。 ,但是在以「宇宙的」大小為準的三角形中,其各角之和就可能不等於這個數字。
- 1.Kulczyck: 《Non-Euclidean Geometry》, chapter 1,
 5 - 5 -  6。 6。
- 2.Struik: 《A Concise History of Mathematics》, Chapter VIII, 18.
|