機率與訊息 (第 4 頁)

　1│2│3│4　

機率與訊息（第 4 頁）

劉豐哲

首頁 | 搜尋

．原載於數學傳播第二卷第三期
．作者當時任職於中研院數學所

‧註釋
‧對外搜尋關鍵字

四、應用

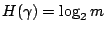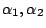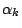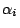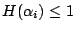(一)我們要利用第三節的概念來回答第一節的彩燈問題。如上所述，m 代表彩燈中燈泡的個數。如果我們用 γ 來表示描述壞燈位置的試驗，則 $H(\gamma)=\log_2m$ 。在第一節中，我們是把測儀的兩根引線接到線路中的兩點以斷定兩點之間有沒有壞燈，這個做法其實也是一個試驗，它的可能結果是壞燈在兩點之間與壞燈在兩點之外。我們來算算至少要檢測幾次才能保證找到壞燈。先假設 k 次可以保證找到。把這 k 次的試驗分別用 $\alpha_1, \alpha_2$ ,…, $\alpha_k$ 表示。由於 $\alpha_i$ 只有兩個可能結果，所以 $H(\alpha_i)\leq 1$ (第三節之(ii))。k 次就能保證找到壞燈的意思是

$\begin{displaymath} I(\alpha_1\vee\cdots\vee\alpha_k, \gamma)=H(\gamma)=\log_2m \end{displaymath}$

由於

$\begin{eqnarray*} I(\alpha_1 \vee \cdots \vee \alpha_k, \gamma) &\leq& H(\alpha... ...lpha_k) \\ &\leq& H(\alpha_1)+\cdots+H(\alpha_k) \\ &\leq& k \end{eqnarray*}$

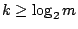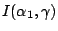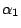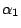所以 $k\geq\log_2m$ 。要使得 k 愈小愈好，就得要求 $I(\alpha_1, \gamma)$ 愈大愈好；用俗話說，就是要使得 $\alpha_1$ 能夠對 γ 提供愈多的訊息愈好。假設在 $\alpha_1$ 中，兩根引線之中有 n 個點，則

$\begin{displaymath} \alpha_1 = \left< \matrix{ A & B \cr \frac{n}{m}& \frac{m-n}{m} \cr } \right>, \end{displaymath}$

其中 A 是指壞燈在兩根引線之內，B 是指在引線之外。因此，

$\begin{eqnarray*} I(\alpha_1 , \gamma) &=& H(\gamma)-H(\gamma\vert\alpha_1)=\log... ...+\log_2m \\ &=& -\eta(\frac{n}{m})-\eta(\frac{m-n}{m})+\log_2m \end{eqnarray*}$

所以我們得到

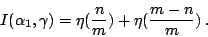$\begin{displaymath} I(\alpha_1 , \gamma)=\eta(\frac{n}{m}) + \eta(\frac{m-n}{m}) \: . \end{displaymath}$

(1)

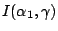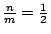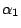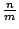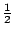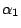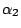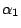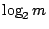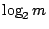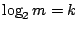(1)式的右邊剛好是一個含有兩個試驗結果的試驗的熵數，因此， $I(\alpha_1, \gamma)$ 的極大是發生在 $\frac{n}{m}=\frac{1}{2}$ 的時候。根據這些，我們知道要使 $\alpha_1$ 發生最大的功用就該使 $\frac{n}{m}$ 儘量的接近 $\frac{1}{2}$ 。譬如說，把 $\alpha_1$ 的兩根引線分接在線路的一個端點與線路的中點（或近似中點）便合乎上面的要求了。這樣做還有一個優點：可以使得 $\alpha_2$ 的情況與 $\alpha_1$ 類似。繼續這樣的測下去，只要測 $[\log_2m]$ 次就能找到壞燈；其中 [ $\log_2m$ ] 是大於或等於 $\log_2m$ 的最小的整數。當 m=2^k 時， $\log_2m=k$ ，和我們起初的結論一樣。

(二)某地有甲、乙兩村，甲村的人只說真話，乙村的人只說假話。兩村村民，你來我往，十分平常。如果你走到了這個地方，卻不知是到了那一個村子，那麼你該怎麼樣的向村民請問，以便儘早知道到底是到了甲村還是乙村？（我們假定你只向第一個碰到的人請教，並假定這人只說「是」與「否」。）你有沒有辦法同時問出這人是甲村的還是乙村的。

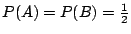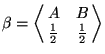首先，我們看看至少要問幾個問題才能確定是到了那一個村子。我們分別用 A、B 表示「到了甲村」和「到了乙村」這兩個事件。因為事先毫無風聲，所以 $P(A)=P(B)= \frac{1}{2}$ 。令 $\beta = \left< \matrix{ A & B \cr \frac{1}{2} & \frac{1}{2} \cr } \right>$ 則這個試驗 β 就描述了「所在何村」這個隨機現象。β 的熵數

$\begin{displaymath} H(\beta)=-\frac{1}{2}\log_2\frac{1}{2}-\frac{1}{2}\log_2\frac{1}{2}=1 \end{displaymath}$

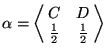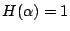假定我們問了某個問句。我們知道村民回答時只可能說「是」與「否」，而且說「是」與「否」的可能性一樣大。令 C 表示「是」，D 表示「否」， $\alpha= \left< \matrix{ C & D \cr \frac{1}{2} & \frac{1}{2} \cr } \right>$ ，則試驗 α 就描述著這個問句所引起的隨機現象。同樣的， $H(\alpha)=1$ 。

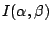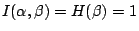依照上面的解釋，我們的目的便是要找一個好的 α，以使得 $I(\alpha,\beta)$ 的值儘量的大。要是能使得 $I(\alpha,\beta) = H(\beta) = 1$ ，那就太好了，那就表示 α 能夠消除 β 的隨機性，α 能夠告訴我們是在那個村子。

我們先看看能不能找到這樣的 α。由於

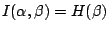$\begin{displaymath} I(\alpha,\beta)=H(\beta)-H(\beta\vert\alpha)=H(\alpha)-H(\alpha\vert\beta) = 1-H(\alpha\vert\beta) \end{displaymath}$

及

$\begin{eqnarray*} H(\alpha\vert\beta)&=&H(\alpha\vert A)P(A)+H(\alpha\vert B)P(B)\\ &=&\frac{1}{2}(H(\alpha\vert A)+H(\beta\vert B)) \end{eqnarray*}$

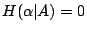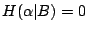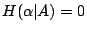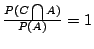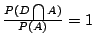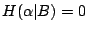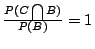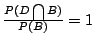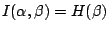$I(\alpha,\beta)=H(\beta)$ 的一個充要條件是 $H(\alpha\vert A)=0$ 及 $H(\alpha\vert B)=0$ 。由於第三節之(i)， $H(\alpha\vert A)=0$ 只發生在 $\frac{P(C\bigcap A)}{P(A)}=1$ 或 $\frac{P(D\bigcap A)}{P(A)}=1$ 的時候。同時的， $H(\alpha\vert B)=0$ 只發生在 $\frac{P(C\bigcap B)}{P(B)}=1$ 或 $\frac{P(D\bigcap B)}{P(B)}=1$ 的時候。因此，我們得到兩個 $I(\alpha,\beta)=H(\beta)$ 的充分條件：

$(1)= \left\{ \begin{array}{c} P(C\bigcap A)=P(A)\\ P(D\bigcap B)=P(B) \end{array}\right.$ $(2)= \left\{ \begin{array}{c} P(D\bigcap A)=P(A)\\ P(C\bigcap B)=P(B) \end{array}\right.$

(1)的意思是說所問的問句必須具有下面兩個性質：

: (a)如果是在甲村的話，問句的答案必須是「是」。
: (b)如果是在乙村的話，問句的答案必須是「否」。

在這樣的指引下，讀者不難看出，「你住在這個村子嗎？」便是一個好問句。只要這麼問一下，便可以知道是在甲村或乙村了。此外，我們只要問一下「一加一是四嗎?」就可知道所請教的人是甲村的還是乙村的。

從上面的討論我們知道兩個問句是夠了，但是，是不是一定要兩個問句呢？

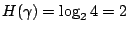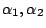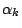我們起初的問題是要用一些問句來判斷下面四個情況中那一個是對的：「在甲村，問甲村人」，「在甲村，問乙村人」，「在乙村，問甲村人」，「在乙村，問乙村人」。在問句提出之前，四個情況都是可能的。我們把這個試驗用 γ 來表示。因此 $H(\gamma)=\log_2 4=2$ 。假設 k 個問句 $\alpha_1, \alpha_2$ ,…, $\alpha_k$ ，可以找出答案，則

$\begin{displaymath} 2=I(\alpha_1\vee\cdots\vee\alpha_k, \gamma)\leq H(\alpha_1\vee\cdots\vee\alpha_k)\leq k \: . \end{displaymath}$

所以至少需要兩個問句。這樣就完全解決了這個問題。

(三)現有九枚外表一模一樣的銅幣。其中一枚是假的。如果我們想要用天平把它找出來，並且確定它是較重或較輕，請問至少要量幾次才辦得到？

所謂用天平來找就是把相同數目的銅幣分別放在天平左右的秤盤上，觀察天平的狀態，是平衡，右傾還是左傾，然後再下判斷。這是一個試驗，它的熵數不會比 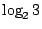$\log_2 3$ 大。

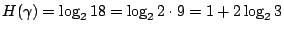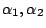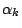我們把找出假幣，並確定它是較重或較輕的試驗用 γ 來代表，因為每一枚銅幣都可能是假的，也都可能較重或較輕，而這些可能性又都一樣大，所以 $H(\gamma)=\log_2 18=\log_2 2\cdot 9=1+2\log_2 3$ 。假設用天平秤 k 次便可找出假幣。我們把這 k 次的試驗分別用 $\alpha_1, \alpha_2$ ,…, $\alpha_k$ 來表示。則

$\begin{displaymath} I(\alpha_1\vee\cdots\vee\alpha_k, \gamma)=H(\gamma)=1+2\log_2 3 \end{displaymath}$

但是

$\begin{eqnarray*} I(\alpha_1\vee\cdots\vee\alpha_k, \gamma) &\leq& H(\alpha_1\v... ...) \\ &\leq& H(\alpha_1)+\cdots+(\alpha_k)\\ &\leq& k\log_2 3 \end{eqnarray*}$

所以

$\begin{displaymath} k\geq 2+\frac{1}{\log_2 3} \end{displaymath}$

也就是說，至少要秤 3 次才行。我們來看看 3 次是不是真的夠了。

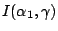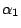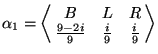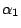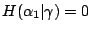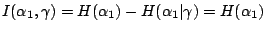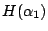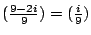首先，我們希望 $I(\alpha_1, \gamma)$ 能夠儘量的大。我們把 $\alpha_1$ 寫成 $\alpha_1 = \left< \matrix{ B & L & R \cr \frac{9-2i}{9} & \frac{i}{9} & \frac{i}{9} \cr } \right>$ 其中 B，L，R 分別表示平衡，左傾與右傾事件，i 表示秤盤上各有 i 個銅幣。由於 γ 可以完全確定 $\alpha_1$ ，所以 $H(\alpha_1\vert\gamma) = 0$ ， $I(\alpha_1, \gamma) = H(\alpha_1)-H(\alpha_1\vert\gamma)=H(\alpha_1)$ 。而 $H(\alpha_1)$ 的極大是發生在 $(\frac{9-2i}{9})=(\frac{i}{9})$ 的時候，也就是 i=3 時。因此，第一次的秤法是在秤盤上各放 3 個銅幣，然後分別考慮：

: (a) B 發生。這時候假幣不在秤盤上，讀者不難看出再量兩次就能找出假幣。
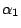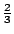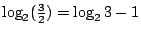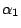: (b) R 發生。這時候假幣在秤盤上。請注意，我們不能丟掉天平右傾這個資料。因為如果丟掉了它，我們從 $\alpha_1$ 得到的就只剩下假幣是在天平上這個事實。這件事發生的機率是 $\frac{2}{3}$ ，因此它所提供的訊息是 $\log_2(\frac{3}{2})=\log_2 3-1$ ，比 $\alpha_1$ 所提供的少了一拍。

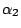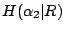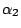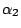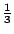現在我們要在 R 為已知的條件下，儘量的把 γ 的隨機性除掉（這時 γ 是六枚銅幣中的試驗）。我們用 $\alpha_2$ 表示第二次的量法。跟以前一樣，我們希望 $H(\alpha_2\vert R)$ 儘量的大；也就是說，在 R 的條件下要求 $\alpha_2$ 能夠提供最多的訊息。因此，在 R 的條件下， $\alpha_2$ 為平衡，右傾及左傾的機率要各為 $\frac{1}{3}$ 。

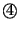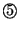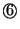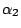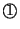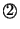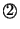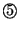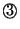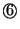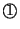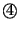為了清楚起見，我們把左邊的三枚分別叫做 $\textcircled{1}$ 、 $\textcircled{2}$ 和 $\textcircled{3}$ ，右邊的三枚分別叫做 $\textcircled{4}$ 、 $\textcircled{5}$ 和 $\textcircled{6}$ ，要使得在 R 的條件下， $\alpha_2$ 為平衡，右傾及左傾的機率一樣，我們可以如下安排：拿掉 $\textcircled{1}$ 和 $\textcircled{2}$ ；把 $\textcircled{2}$ 和 $\textcircled{5}$ 相互交換；保持 $\textcircled{3}$ ， $\textcircled{6}$ 不動。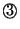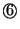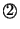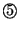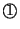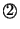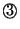在這樣的量法之下，如果天平是平衡的，則假幣便在 $\textcircled{1}$ 與 $\textcircled{4}$ 之中；如果天平仍舊右傾，則在 $\textcircled{3}$ 與 $\textcircled{6}$ 之中；如果天平變為左傾，則在 $\textcircled{2}$ 與 $\textcircled{5}$ 之中；而且，如果假幣在 $\textcircled{1}$ 、 $\textcircled{2}$ 、 $\textcircled{3}$ 之中，則假幣比真幣輕，否則比真幣重。根據這些，再量一次便可完全解答原來的問題。

: (c) L 發生。論法與(b)相同。

因此，量三次便可完成鑑定工作。

本節所討論的例子雖然都是趣味性的問題；但是已經表現出了訊息論的一般用法。較嚴肅的應用問題（如訊息傳遞的工程問題），常常可以仿照第三節來處理，只是可能比較複雜，須要更精細的分析。以後有機會時，我們再介紹一些訊息論在訊息傳遞問題上的簡單應用。

　1│2│3│4　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：黃信元

最後修改日期：4/26/2002