機率與訊息 (第 3 頁)

　1│2│3│4　

機率與訊息（第 3 頁）

劉豐哲

首頁 | 搜尋

．原載於數學傳播第二卷第三期
．作者當時任職於中研院數學所

‧註釋
‧對外搜尋關鍵字

三、試驗的熵數

現在我們要簡單地討論訊息論裏最根本最重要的概念──試驗的熵數。至於它的應用，則要到下一節再討論。

假定我們現在用某個試驗來觀察一個特定的隨機現象，我們自然會問自己：能不能找到一個適當的量來度量該試驗所能提供的訊息 (Information)？換一個角度來看，在試驗之前，我們無法預知會出現什麼結果，因此我們說試驗具有隨機性；試驗之後我們知道結果了，隨機性就消失了，消失了的隨機性可以看成是我們所獲得的訊息。所以，事實上，我們等於在問：能不能找到一個適當的量來度量該試驗的隨機性？

假定 A₁, A₂,…,A_n 是某個試驗的所有可能結果。如果 P(A_i) > P(A_j)，則「A_j 出現」比「A_i 出現」要使我們驚奇，就如像稀有的社會事件具有非常的新聞價值一樣。也就是說，機率不同的結果會提供不同的訊息。因此，用來量度該試驗所能提供的訊息（或試驗的隨機性）的那個量，必須是各個結果所提供的訊息的某種平均值。首先，我們來看看如何度量個別事件所能提供的訊息。我們假定有一個這樣的量，而用 I(A) 來代表事件 A 所能提供的訊息，則 I(A) 應當滿足：

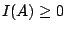: (1) $I(A)\geq 0$ ；
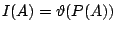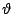: (2) I(A) 完全由 A 的機率決定，換句話說， $I(A) = \vartheta(P(A))$ ， $\vartheta$ 是個定義在 0 到 1 之間的函數；
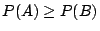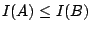: (3) 如果 $P(A)\geq P(B)$ ，則 $I(A)\leq I(B)$ 。

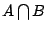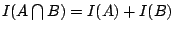條件(1)僅僅表示取定一個適當的準點；條件(2)是強調機率的特點，我們說過事件的隨機規律性是由它的機率來代表的，因此和事件有關的重要數量也該是完全由事件的機率來決定。現在我們進一步考慮兩個獨立事件 A 和 B。 $A\bigcap B$ 可以解釋為在 A 出現的情況下，B 又出現的事件，但是 A 和 B 是獨立的，由 A 出現所得到的訊息，應該無法幫助我們預測 B 出現的可能性，因此已知 A 出現後，又知道 B 出現所提供的訊息，應當為 A,B 各別出現所得訊息之和，亦即 $I(A\bigcap B) = I(A)+I(B)$ 。相應地，我們要求 $\vartheta$ 滿足：

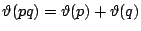: (4) $\vartheta(pq)=\vartheta(p)+\vartheta(q)$ , $p,q \in[0,1]$

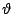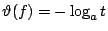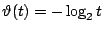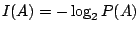將(1)、(2)、(3)，和(4)綜合起來，就是一個定義 [0,1] 在上、滿足(4)的遞減函數 $\vartheta$ 。這種函數很多，譬如說， $\vartheta(f)=-\log_a t$ ， $t \in[0,1]$ ，a 為某個正實數。這兒取不同的 a 僅僅表示選取不同的單位長度。在下面，我們取 $\vartheta(t)=-\log_2t$ ，也就是令 $I(A)=-\log_2P(A)$ 。

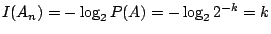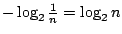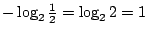在進一步討論試驗的訊息之前，我們回頭看看1.的例子。我們有 2^k 個燈泡，其中一個壞了；在檢測之前，我們認為每個燈壞的機率都是一樣的，都是 2^-k。令 A_n 為第 n 個燈泡壞了的事件，則 $I(A_n) = -\log_2 P(A)=-\log_2 2^{-k}=k$ 。這時，測出任何一個壞燈所能提供的訊息皆為 k，因此 k 度量著測出壞燈位置所獲得之訊息，也就是壞燈位置的隨機性。一般來說，如果試驗中的每個結果具有同樣的可能性（出現的機率一樣），則 $-\log_2 \frac{1}{n} = \log_2 n$ 代表著該試驗所提供的訊息，其中 n 是所有可能結果的個數。譬如說，丟擲一枚非偏倚銅板，觀察正面成反面出現所得的訊息為 $-\log_2 \frac{1}{2} = \log_2 2=1$ 。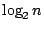歷史上，第一個考慮試驗熵數的人是美國電訊工程師 Hartley（1928年），他把試驗熵數定義為 $\log_2 n$ 。他只考慮到試驗中可能出現的結果的個數，卻忽略了每個結果出現的機率。這個概念在 1947～1948年間由顯農氏予以修正，而成了目前數學家和工程師所採用的形式。

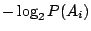假定 A₁,A₂,…,A_n 是某個試驗的所有可能結果。我們知道事件 A_i 所能提供的訊息是 $-\log_2 P(A_i)$ 。因此，觀察一次試驗所得到的訊息是個隨機變數。這個隨機變數的期望值就是多次獨立觀察該試驗所得的訊息的平均值。顯農氏把這平均值叫做試驗的熵數。形式上說，如果

$\begin{displaymath}\alpha=\left< \begin{array}{ccc} A_1,&\cdots&,A_n\\ P(A_1),&\cdots&,P(A_n) \end{array}\right> \end{displaymath}$

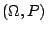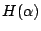是機率空間 $(\Omega ,P)$ 的一個試驗，則 α 的熵數 $H(\alpha)$ 是定義為

$\begin{displaymath}H(\alpha)=-\sum_{i=1}^nP(A_i)\log_2 P(A_i) \: .\end{displaymath}$

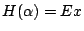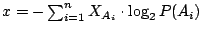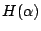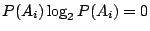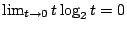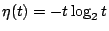如果我們用 X_B 表示 Ω 中事件 B 的指示函數，則 $H(\alpha) = Ex$ ，其中 $x=-\sum_{i=1}^nX_{A_i}\cdot\log_2P(A_i)$ 。要是在 $H(\alpha)$ 的定義中，某個事件 A_i 的機率 P(A_i)=0，則令 $P(A_i)\log_2P(A_i)=0$ 。這是有道理的，因為 $\lim_{t\rightarrow 0}t\log_2 t=0$ ，另外，如果我們令 $\eta(t)=-t\log_2 t$ 可以簡單的寫成

$\begin{displaymath} H(\alpha)=\sum_{i=1}^n\eta(P(A_i)) \: . \end{displaymath}$

好了，在這些緊湊的抽象討論後，我們來回頭看看那串彩燈吧！依照上述的符號，我們要問的是試驗

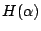$\begin{displaymath} \alpha=\left< \begin{array}{ccc} A_1,&\cdots&,A_{2^k}\\ (\frac{1}{2})^k,&\cdots&,(\frac{1}{2})^k \end{array}\right>\end{displaymath}$

的熵數 $H(\alpha)$ 。根據剛才的定義。

$\begin{displaymath}H(\alpha)=-\sum_{i=1}^{2^k}\eta(P(A_i))=k ,\end{displaymath}$

這正是我們最初的意思。

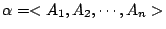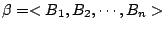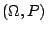試驗的熵數具有下述性質：假設 $\alpha=<A_1,A_2,\cdots,A_n>$ , $\beta=<B_1,B_2,\cdots,B_n>$ 為機率空間 $(\Omega ,P)$ 的兩個試驗，則

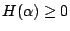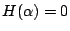: (i) $H(\alpha)\geq 0$ ; $H(\alpha)=0$ 的充要條件是某個 A_i 為必然事件，而其餘的均為不可能事件。
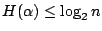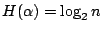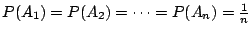: (ii) $H(\alpha) \leq \log_2 n$ ; $H(\alpha)=\log_2 n$ 的充要條件是 $P(A_1)=P(A_2)=\cdots=P(A_n)= \frac{1}{n}$ 。
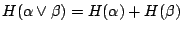
: (iii) 如果 α 和 β 是獨立的，則 $H(\alpha\vee\beta) = H(\alpha) + H(\beta)$

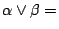
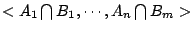(i)的證明很簡單，(ii)的證明與機率無關，因此，我們略掉它們，而來證明(iii)。根據定義， $\alpha\vee\beta =$ $<A_1\bigcap B_1, \cdots, A_n \bigcap B_m>$ 。由於 α 與 β 是獨立的，

$\begin{displaymath}P(A_i\bigcap B_j)=P(A_i)P(B_j)\end{displaymath}$

因此

$\begin{eqnarray*} H(\alpha\vee\beta) &=& -\sum_{i,j}P(A_i\bigcap B_j)\log_2P(A_i... ...beta)\mbox{{\fontfamily{cwM0}\fontseries{m}\selectfont \char 1}} \end{eqnarray*}$

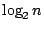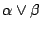性質(i)可解釋為：如果在某試驗中，會有一個必然事件產生，則觀察這個試驗是不會提供任何訊息的，也就是說，這個訊息沒有隨機性。當著試驗中的各個事件具有同樣的機率時，我們把它叫做非偏倚試驗。性質(ii)告訴我們，在具有 n 個事件的試驗中，非偏倚試驗的隨機性最大，其熵數為 $\log_2 n$ 。這是合乎直覺要求的；因為，在觀察偏倚試驗時，我們是預先就知道了某些事件比較容易發生，而另一些事件是比較不容易發生；這種含糊的預知就說明了偏倚試驗的隨機性比較小。其實，如果偏倚到了極點，就沒有隨機性了，而這正是性質(i)所要描述的。依照前而的說法， $\alpha\vee\beta$ 指的是同時觀察 α 和 β 兩個試驗，依此，性質(iii)可以如下敘述：如果 α 和 β 是獨立的試驗，則同時觀察 α 和 β 所得的訊息為分別觀察 α 和 β 所得訊息的和。總結起來，我們所定義的試驗的熵數的確是描述了我們所預期的各項簡單性質，這些就注定著它會是一個重要而有用的概念。

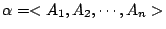在介紹熵數的其他性質之前，我們先談談條件熵數。假設 $\alpha=<A_1,A_2,\cdots,A_n>$ 為一試驗，B 為一事件。則

$\begin{displaymath}\left< \begin{array}{ccc} A_1\bigcap B,&\cdots&,A_n\bigcap B\\ P(A_1\bigcap B),&\cdots&,P(A_n\bigcap B) \end{array}\right> \end{displaymath}$

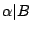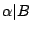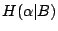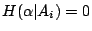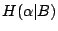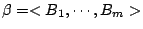也可以看成一個試驗。這個試驗是在 B 已經發生的情況下來觀察 α 的試驗。我們把這個試驗記為 $\alpha\vert B$ 。試驗 $\alpha\vert B$ 的熵數 $H(\alpha\vert B)$ 表示看在事件 B 已經發生的情況下，試驗 α 所留存的隨機性。例如 B=A_i，則在 A_i 出現的情況下，α 已不具有任何隨機性，因此 $H(\alpha\vert A_i)=0$ 。（這點可以很容易的從性質(i)導出。） $H(\alpha\vert B)$ 稱為試驗。相對於事件 B 的條件熵數。假設 $\beta=<B_1,\cdots,B_m>$ 為另一試驗，令當

$\begin{displaymath} x=\sum_jX_{B_j} H(\alpha\vert B_j) \: . \end{displaymath}$

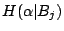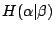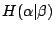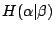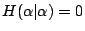B_j 發生時，x 就是 $H(\alpha\vert B_j)$ 。我們把 x 的期望值記為 $H(\alpha\vert\beta)$ 。 $H(\alpha\vert\beta)$ 量度的是在觀察了試驗 β 之後，α 所留存下來的隨機性。我們把 $H(\alpha\vert\beta)$ 叫做 α 相對於 β 的條件熵數。顯然的， $H(\alpha\vert\alpha)=0$ ，熵數的另外兩個重要性質是：假設α,β 是兩個試驗，則

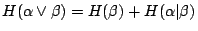
: (iv) $H(\alpha\vee\beta)=H(\beta)+H(\alpha\vert\beta)$
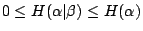
: (v) $0\leq H(\alpha\vert\beta)\leq H(\alpha)$

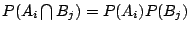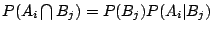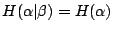性質(iii)是性質(iv)的特例，而性質(iv)的證明又跟性質(iii)的完全一樣，只要把 $P(A_i\bigcap B_j) = P(A_i)P(B_j)$ 換成 $P(A_i\bigcap B_j)=P(B_j)P(A_i\vert B_j)$ 就行了。性質(v)的證明與機率概念無關，所以省略。不過，我們要提醒讀者一點：在直覺上，性質(v)是極為顯然的，因為在觀察 β 之後，我們多多少少會得到些訊息，這些訊息只可能減少 α 的隨機性。另外，從(iii)和(iv)可以看出，如果 α 和 β 是獨立的，則 $H(\alpha\vert\beta)=H(\alpha)$ 。

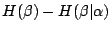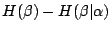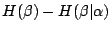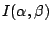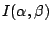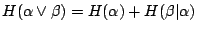
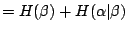從上段的討論可以看出 $H(\beta)-H(\beta\vert\alpha)$ 量度的是試驗 β 在觀察了試驗 α 之後所減少的隨機性。因此，我們可以把 $H(\beta)-H(\beta\vert\alpha)$ 看成是 α 提供給 β 的訊息。我們把 $H(\beta)-H(\beta\vert\alpha)$ 記為 $I(\alpha,\beta)$ 。有時候 $I(\alpha,\beta)$ 叫做 β 存於 α 中的訊息。由於 $H(\alpha\vee\beta) = H(\alpha)+H(\beta\vert\alpha)$ $=H(\beta)+H(\alpha\vert\beta)$ ，我得到下面的關係式：

$\begin{displaymath} I(\alpha, \beta)=H(\beta)-H(\beta\vert\alpha)=H(\alpha)-H(\alpha\vert\beta)=I(\beta, \alpha) \end{displaymath}$

在應用的時候，β 是我們要研究的對象，α 是為了消除 β 的隨機性而考慮的輔助試驗。這些都將在下面詳細討論。

　1│2│3│4　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：黃信元

最後修改日期：4/26/2002