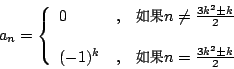| |
在提出「生成函數」的數學定義之前,我們先考慮幾個簡單的排列組合問題。
- [例 a.1]考慮恆等式
(1+ax)(1+bx)(1+cx)=1+(a+b+c)x+(ab+bc+ac)x2+abcx3
如將 a,b,c 看作代表三物件,它的右邊是一多項式,其係數恰代表了將 a,b,c 作組合的各種可能。常數項 1 表示在三物件中一個都不取;x 的係數 a+b+c 表示在 a,b,c 中取一個的各種組合,即或取 a,或取 b,或取 c;x2 的係數 ab+bc+ac 表取二個的各種組合;x3 之係數表示了三個皆取的唯一方法。在這裏可能產生各種情形是用 + 號連接,同時發生之事件則用乘法(即符號併列)表示。
- [例 a.2]設有 5 個球 a,a,a,b,c,其中三個球 a 完全一樣,則恆等式
其中 xr 之係數表示了選取 r 個的各種可能組合 (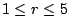 )。 )。
在排列組合問題中,加法原則與乘法原則是大家熟知的兩個法則。加法原則是講如一事件可能發生情況有 m 種,另一種事件可能發生情況有 n 種,則這兩種事件其一發生情況有 m+n 種。乘法原則是講如一事件可能發生情況有 n 種,另一事件可能發生情況有 m 種,則這兩事件同時發生情況有 nm 種。我們在上面兩例用到的是一種符號運算,它遵從這兩法則。在 [例 a.2],因子
1+ax+a2x2+a3x3 表示了或不取 a,或取一個 a,或取 2 個 a,或取三個 a 的各種情況;而在 [例 a.1] 中,(1+ax)(1+bx) 表示了如果 a,b 被允許同時選取時可能產生之各種情況。
在很多場合中,我們只對事件發生可能之個數有興趣,而不在乎事件發生的具體形式。這時我們可以取代表不同物件的符號 a,b,c 等均為 1,例如在 [例 a.1] 中,令 a=b=c=1,則
(1+x)(1+x)(1+x)=1+3x+3x2+x3
其中 xr 之係數為在三個物件中取 r 個的組合數。
- [例 a.3] 我們所熟知的兩項公式
中之 xr 係數恰是在 n 個中取 r 個組合數。當然如果 r>n 則
 . .
現在我們提出「生成函數」的數學定義。
- 定義
- 設
 是一數列,則函數 是一數列,則函數
稱為數列
 之(普通)生成函數 (ordinary generating function) 或組合生成函數 (generating function for combination)。 之(普通)生成函數 (ordinary generating function) 或組合生成函數 (generating function for combination)。
在 [例 a.3] 中,(1+x)n 是數列
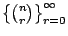 之生成函數。我們看到要從 n 個物件中取 r 個的組合數問題與其生成函數 (1+x)n 的係數有一種對應關係存在。
之生成函數。我們看到要從 n 個物件中取 r 個的組合數問題與其生成函數 (1+x)n 的係數有一種對應關係存在。
- [例 a.4]
設有 n 個物件,並設 n(r) 是由 n 個不同物件中可任意重複地取 r 個物件生成函數的組合數
原編註 1
。這個組合問題的生成函數即是「xr 之係數等於 n(r)」之生成函數。對一個物件來說,我們可以不選取,選取一次,選取二次等等,其方法可用式子
表示。對第二個,第三個等物件也有同樣作法。故其生成函數是
我們必須將它寫成標準形式。因為
故
我們得
- [例a.5]
設 n(r) 是由 n 個不同物件中可任意重複地取 r 個,並在每一選取中,每個物件必須至少包含一次的組合數
原編註 2
。數列 {n(r)} 的生成函數是
故得
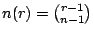 。顯然如果 r<n,本問題無解。 。顯然如果 r<n,本問題無解。
簡單推廣上述問題,若在每一選取中每個物件必須至少選取 q 次,則
一般排列組合問題可以歸納成將球放入盒中的問題。其中可將球與盒子看成可區分的或不可區分的,而每一盒子又可被允許放最多一個球,或超過一個球而產生各種情況。組合問題可看成將不可區分的球放入可區分的盒中之問題。例如 [例 a.4] 的問題相當於想求得將 r 個相同的球,可任意重複地放入 n 個不同盒中之方法個數。[例 a.5] 的問題相當於要求出將 r 個相同的球放入 n 個不同盒中之方法個數,其中每一盒必須至少放一個球。放球入盒的各種情況可列表如下:
| |
a |
b |
c |
d |
| 球 |
不可區分(r) |
可區分(r) |
可區分(r) |
不可區分(n) |
| 盒 |
可區分(n) |
可區分(n) |
不可區分(n) |
不可區分(r) |
| 典型問題 |
組合 |
排列 |
集合之分割 |
整數之分解 |
其中 n 或 r 表示盒子的個數,或球的個數。下面我們將利用生成函數的方法討論這四類問題。
- [例 a.6]
設將相同的球放置於 n 個不同盒中,其中每一盒至少放 q 個球,並至多放 q+z-1 個球。此問題之生成函數是
使問題具體些。設有四人擲骰,每人各擲一次,問當所得點數之和為 17 時共有多少種可能方式。四人可看作四個相異的盒子,17 點可看作 17 個相同的球。這問題是當 n=4,r=17,q=1,z=6 之特別情況。故答案為
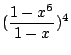 展開式中 x13 項之係數,即共 104 種。 展開式中 x13 項之係數,即共 104 種。
上面我們利用組合生成函數求解了一些組合問題。顯然組合生成函數並不適用於排列問題。例如設 a,b 為兩物件,其全排列是 {ab,ba} 直接應用上面求組合問題的方法,我們必須有
(1+ax)(1+bx)=1+(a+b)x+(ab+ba)x2
此式在我們熟知的數學運算法則中顯然不成立。但在求排列數問題中,我們仍然可以保留上面用到的思考方法與步驟,只要將普通生成函數用所謂指數生成函數來代替。
- 定義
- 設
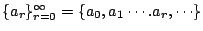 是一數列,則函數 是一數列,則函數
稱為
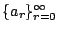 之指數生成函數 (exponential generating function) 或排列生成函數 (generating function for permutation)。 之指數生成函數 (exponential generating function) 或排列生成函數 (generating function for permutation)。
- [例 b.1]
設 p(n,r) 為在 n 個物件中無重複地取 r 個的排列數。因為
(1+x)n 是數列
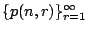 之排列生成函數。顯然 r>n,我們有 p(n,r)=0。我們注意到這問題相常於「將 r 個不同的球放置於 n 個不同盒中」的問題,其中每盒最多放置一個球。 之排列生成函數。顯然 r>n,我們有 p(n,r)=0。我們注意到這問題相常於「將 r 個不同的球放置於 n 個不同盒中」的問題,其中每盒最多放置一個球。
- [例 b.2]
有 p+q 個物件,其中 p 個為相同,q 個亦為相同,取全排列。此問題相當於 p+q 相異之球放置於兩異盒中,第一盒恰好放 p 個球,第二盒恰好放 q 個球。其排列生成函數
得其排列數是
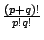 。此為大家所熟知的。 。此為大家所熟知的。
具體一些,令 a,a,a,b,b 為五物件,其中三物相同,二物為相同作排列。對 a 言可以不選取,取 1 個,取 2 個或取 3 個等。對 b 言可以不選取,取 1 個或取 2 個等。其排列生成函數為
由此得在 a,a,a,b,b 中作 4 個排列之個數為
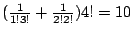 。 。
- [例 b.3]
在 n 個相異物件中作可以任意重複之排列。其排列生成函數為
故得在 n 個相異物件中取 r 個作可以任意重複之排列數為 nr。
-
- [例 b.4]
將整數 0,1,2,3 取來作 r 位數字,並設 p(r) 是在每一數字中 1,2 與 3 每一個至少出現一次之 r 位數字個數,對於整數 0 而言可以不取,取一個,取二個……等等,此方法可用式
表示。對於 1,2,3 每個而言,則必須至少取一個,此方法可用下式
表示。故數列 {p(r)} 之排列生成函數為
因此
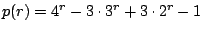 。 。
- [例 b.5]
將 r 個不同的球放入 n 個不同的盒中,每盒至少放一個。本問題的排列生成函數為
故得所求之排列數為
顯然如果 r<n,本問題則沒有解。
現在我們簡短討論第三類有關集合的分割問題。一集合之分割是將此集合表達成其諸兩兩不相交之子集合的併集。分割中的每一子集合稱為一類。例如在一班學生中,按年齡分組便是一個班級的分割,同年的學生便形成了一類。
- [例 c.1]設某一集合有 r 個元素,並設
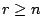 ,將這集合表達成 n 個非空子集合之分割相當於將 r 個可區分的球放置於 n 個不可區分的盒中,其中每盒至少含有一球。顯然如果 r<n,則本問題沒有解。將 r 個元素的集合分割成 n 個非空子集合的方法數是用 S(n,r) 表示,在數學上是一個很重要數字,稱為第二類 Stirling 數,本例與 [例 b.5] 不同處是將盒子看成相同了,故得 ,將這集合表達成 n 個非空子集合之分割相當於將 r 個可區分的球放置於 n 個不可區分的盒中,其中每盒至少含有一球。顯然如果 r<n,則本問題沒有解。將 r 個元素的集合分割成 n 個非空子集合的方法數是用 S(n,r) 表示,在數學上是一個很重要數字,稱為第二類 Stirling 數,本例與 [例 b.5] 不同處是將盒子看成相同了,故得
如果在分割時允許有空類存在,則當 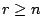 時,它的方法數是 時,它的方法數是
當 r<n 時,其方法數是
最後我們介紹一些整數分解的問題。一種整數 n 的分解,是一種將 n 表達成整數和的方法:
因僅是被加數次序不同的和是看作相同的分解,我們可以假定
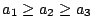 … …
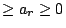 。每一被加數 ai 稱為這分解的一個部分。一種整數 n 的分解成 r 部份的和相當於將 n 個相同的球放置於 r 個相同的盒中(為了習慣上用法,我們交換了 n 與 r 所代表的意義)。因球是看作不可區分的,我們需用組合生成函數探討此類問題。 。每一被加數 ai 稱為這分解的一個部分。一種整數 n 的分解成 r 部份的和相當於將 n 個相同的球放置於 r 個相同的盒中(為了習慣上用法,我們交換了 n 與 r 所代表的意義)。因球是看作不可區分的,我們需用組合生成函數探討此類問題。
- [例 d.1]
對整數作分解,其每一部份不得超過 r,在其分解之部份中,整數 1 可不出現,或出現 1 次,或出現 2 次……等等,其方法可用式子
表示。同樣整數 2 可不出現,或出現 1 次,或出現 2 次,……等等,其方法可用式
表示。依此類推,對整數 r 同樣可不出現,或出現 1 次,或出現 2 次,……等等,其方法可用式
表示,故整數之部份不超過 r 之分解之生成函數是
上式展開式中 xn 之係數便是整數 n 之部份不超過 r 的分解個數。顯然如果 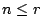 ,在任意 n 的分解中都不會出現大於 r 的部份,故它就是所有整數 n 之分解之個數。 ,在任意 n 的分解中都不會出現大於 r 的部份,故它就是所有整數 n 之分解之個數。
- [例 d.2]
任意一種整數之分解均可用Ferrers 圖示來表示,設 n=14,則我們有下面兩種 14 的分解和與其對應的 Ferrers 圖示:
其中行數表示部份之個數,最大的列數表示最大的部份。如果我們將上兩圖沿對角線轉摺,左右兩圖便互換位置。這種互換建立了一種部份不超過 r 的分解與部份之個數不超過 r 的分解間一一對應關係,故得:一整數之部分不超過 r 之分解個數等於部份個數不超過 r 的分解個數。
利用 [例 d.1] 之結果我們得到一整數之恰有 r 個部份之分解之生成函數是
- [例 d.3]
利用 Ferrers 圖示間的轉摺對應關係,我們還可以得到如下結論:分解一個整數 n 時,以 r 為最大部份的分解方法和以 r 為部份個數的分解方法一樣多。故得整數之恰有 r 個部份之分解的生成函數是
此結果與由 [例 d.2] 所得完全一樣。
- [例 d.4]
如果
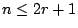 ,則 xn 在 ,則 xn 在
中的係數是將 n 分解成奇數部份的分解個數;如果 n>2r+1,則 xn 的係數是 n 的部份是奇數且不超過 2r+1 的分解個數。
如果 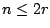 ,則 xn 在 ,則 xn 在
中的係數是將 n 分解成偶數部份的分解個數;如果 n>2r 則 xn 的係數是 n 的部份是偶數且不超過 2r 的分解之個數。
如果 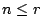 ,則 xn 在 ,則 xn 在
中的係數是整數 n 之部份各不相同的分解個數;如果 n>r,則 xn 的係數是 n 之部份各不相同且不超過 r 的分解個數。
因為我們有恆等式
故一整數分解成部份兩兩相異之個數等於分解成奇數部份之個數。
- [例 d.5]
恆等式
表示任意整數均可唯一地表示成 2 的冪的和形式,其中各項均相異。
整數分解的問題常以求一次不定方程之整數解個數形式出現,下面便是一個簡單的例。
- [例 d.6]
求一次不定方程 x+y+z=15 且滿足
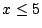 , ,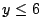 , ,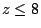 之正整數解之個數。 之正整數解之個數。
滿足上面條件的正整數解之個數是 x15 在生成函數
中的係數,其答案是 15。
作為本文最後的一個例,我們利用組合問題與其生成函數之對應關係證明下面著名的 Euler 恆等式:
其中,
首先我們要有下面結果:
- [例 d.7]
設 n 是一正整數,令E(n) 表示將 n 分解成偶數個部份均不等之分解個數;F(n) 表示將 n 分解成奇數個部份均不等之分解個數,則我們有
上式是利用 Ferrers 圖示所產生的對應來證明。設某一 n 之部份相異之分解的圖示有如左圖(我們用 23=7+6+5+3+2 為例):
令 b 記作底線上方框個數,d 記作 45°斜線上方框個數。這裏有三種情況:
- 如果 b<d,
則底線上 b 個方框可移至斜線上端如右圖所示。這樣 n 之分解中部份個數則減少了一個,且各部份仍保持相異。
- 如果 b=d,
則底線方框仍可移至斜線上端,唯一例外是斜線和底線相交如下面左圖:
在這情況下,這分解有形式
- 如果 b>d,
則斜線上方框可移至底部而令分解之部份個增加一個並各部份仍保持相異,唯一例外是斜線和底線相交如上面右圖且 b=d+1 在這情況下,這分解有形式
當
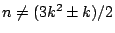 時,上面對應使 E(n) 與 F(n) 相等;當 時,上面對應使 E(n) 與 F(n) 相等;當
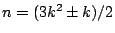 時,則 k 是偶數使 E(n) 比 F(n) 多一個;k 是奇數使 E(n) 比 F(n) 少一個。本例證畢。 時,則 k 是偶數使 E(n) 比 F(n) 多一個;k 是奇數使 E(n) 比 F(n) 少一個。本例證畢。
回到我們上面提到之 Euler 恆等式。它的左邊是一無窮乘積,恰是數列 {E(n)-F(n)} 的生成函數。由 [例 d.7] 我們證明了 Euler 恆等式。
生成函數在數學各分枝及其它各學科中有廣泛應用,本文僅就它在排列組合問題上應用作一粗淺介紹。在這裡,生成函數是看成一代數對象,我們無須顧慮它的收斂性,其理論基礎請參閱參考資料4。生成函數在概率論中應用在1中有討論,進一步有關整數分解的資料可在2中找到。有關一般性生成函數在組合學中的應用請參閱3,5。
- 1. Feller, E.F., 《An Introduction to Probability Theory and Its Application》, Vol.I, John Wiley & Sons, 1968.
- 2. Hardy, G. H. & Wright, E.M., 《An Introduction to Theory of Numbers》, Oxford Univerdity Press, 1960.
- 3.Liu, C.L., 《Introduction to Combinatorial Mathematics》, McGraw-Hill, 1968.
- 4. Niven, I, 《Formal Power Series》, Amer. Math. Monthly, 76 (1969), 871-889.
- 5. Riodan, J.,《An Introduction to Combinatorial Analysis》, John Wiley & Sons, 1958.
|
|
對外搜尋關鍵字:
.生成函數
.第二類Stirling數
|