|
�S�������]�A�]�ΨH�q�̥�Ϊ��@�d�s�@���Ȧ�^ |
�ڦ^�a�ܿ�A�O�w�wù�̹F�P���Ѽֳ����E�|���`��b�]���G�C�o�@��]�ڳQ�c�کҧx�Z�C�ڹڨ��]�U�@���e�j���Ǫ��A�M��S�ڨ��A�ר��P���Ħ��ҡA�b���ǥi�Ȫ����������A�ڤ����D�p����}���ӷ|�N�H�ܦ������Ϊ������F�M��K�K�C��M�@�ӹq�ܨϧ���^�{��A���O�ڪ��ѪB�ͭݬP�ڮȦ���j����б¥��Ӫ��C
�L���G�u�˷R����ΡA���@�Ӻ�檺���D�o�ͤF�A�Ѥ�Ǯa�o�{�t�z���X�{�@�ө_�Ǫ�����w�w�@���������½u�Ѥ@�ӻȪe�t������t�@�Ȫe�t�C�S���H���D�쩳�O���^�ơA�Y�Ϧb���b�W�ˤW�̦n���滷��M�L�u�q�滷��]�L�k�����o�����C�A�O�ڭ̳̫᪺�Ʊ�F�C�ִµ۬P�� ACD-1587 ����V�_���a�v�C
����ڱq�ײz�t���^�ڪ��¥��l���b�A�P�ɸˤW�ɶ��[�t���M�q�l�����H�C�o�����H���o�t�z���Ҧ��y���M�Ҧ������P�ڮȦ檺�G�ơ]�b�ȳ~���O�ү�ϧڮ����ܤ֤��~���[�^�C��O�ڴN�_������ڪ����ȤF�C
���������H�������Ҧ����G�ƦӶ}�l���Ʊԭz���ɭԡ]�A�S����ť�@�ӹq�l�����H���ƦѬG�ƤQ�����������ƤF�^�A�ڮȵ{���ؼдN��{�b�������a��F�C���Ǫ��������w�w���Ȫe�t�w���b�ڨ���A�e�{�b���e���O�K�K�t�z�j�����C�e�Ǯɧڳy�F�@�Ӥp��P�A�Ѩ��ǬP�ڶ����C���y�`�̦��J�C���L�̧⥦����F�A�A�y�����ҡC��ӥL�̨M�w���A�C�C���ͪ��Ȫe�t�A��O�\�_�F�@�ɻ��ا������ؿv���w�w���t�z���Ҧ��ȹC�̪����]�A�s���t�z�j�����C�o�������X�G�Ҧ����Ȫe�t�C�ڻ��u�X�G�Ҧ��v�O�]���y�`�̤w�g��ּƯ���Ȫe�t���馨�s�s�������P�s�C
�j�����˿X�o�ܯ��_�C�C���и˦��N���q�ߤ��s�Y�C�]�إ𮧮ɡA���p�A�@�N�����٥i�H��ۤv���Ѧ��q�l�A���W�h���̨ͪӧ�A����l�զX����Ӫ��A�C
�������̭��n���S��O���L�a�h�өж��C�y�`�̧Ʊ�q���H�ᤣ�|�Ať�쨺�O�H�дo���@�y�ܡu�S���ũж��v�A�o�ܱq�@�}�l���C�N�x�Z�ۥL�̡C
�Y�ϳo�������o�S��A�ڪ��B���٬O���ΡC�@���i�����e�U�A�N�ݨ���ܵP�W�g�ۡG�t�z�ʪ��Ƿ|���N���b�@�ʤG�Q�C�h�ӵn�O�C
�ѩ�t�z�ʪ��Ǫ̨Ӧ۩Ҧ��Ȫe�t�A�ӻȪe�t�S���L�a�h�ӡA��O�Ҧ����ж����Q�Ƿ|�X�u�̩ҥe���A�]���S���ũе��ڡC�z���յۻ��A�Y�ǥN�����ڻP�L�̦��b�@�_�C�����ڵo�{�@�N���H���A�@�өI�l���O�t��A�t�@�ӫh���w��ǷŽը� 860�K �����ҮɡA�ڥu�n���¥L�̪����N�C
���n���ƪ��]�O�Ӭy�`�̡A�L�ٰO�o�ڵ��L�M�L���P�M�����f�C�L�n�Q��k�w���ڤ@�Ӧ�m�A�]���b�P�ڤӪŤ��L�]�O�|�o�ͪ����C�H����褧��A�L��V�z���G
�u��L�w�m�b�@���Сv�C
�u�@���Ъ��ЫȤS�w�m�쨺�ةO�H�v
�u��L�E��G���СC�G���Ъ��ЫȾE��T���СA�T���Ъ���|���СA�̦������C�v
�N�b���ɧڤ~�}�l��|�o���]�����M�`�S�ʡC���]�o���]�Ȧ������өж��A�h�̫�ж����ЫȰȥ��Q���h�X�Ӧ���P�ڤӪťh�C���N�]�����]���L���h�өж��A�ҥH�گ�h�i�h�Ӥ���ܥ���t�z�ʪ��Ǯa�����]�����|�C
�ĤG�Ѧ�����ڵo�{�ڥ��ݾE��Ĥ@�ʸU���ЮɡA�ڤ]���P����Y�F�C����M���A���O�]���S�� 999,999 ��ȤH�n���i���]�C�o�ǿ��̬O�q�Ȫe�t VSK-3472 �Ӫ��t�z�ʪ��Ǫ̡C�ĤT�ѷ��ڥI���]�O�ɡA����Y�a�o�{���رƤF�@�����s�A�q�z�������f���ƨ차�N�۪����h������C���ɧ�ť��@���n�����G
�u���@�N�Ψ�T�w�wù�̹F�P�����l�����@�T��Q�������l���C�v
�u�֦��t�z�ɥN�Ĥ��Q�C�~���k�����w�l���H�v
�ڰg�b���ݺz���G
�u�o�ǤH�O�֡H�v
�u�L�̬O�P�ڶ��l�a�C�v
�u�L�̤H�ܦh�ܡH�v
�u�L�a�h�w�w�C�@�Ȫe�t�@�ӥN���C�v
�u���O�A�p����L�̧��ж��H�A���A�t�z�ʪ��Ǯa�n����Ѥ~���}�O�I�v
�u�ڤ����D�F�ڥ��n���o�ƥh�би��ƪ��X�����C�v
�M�ӳo�������D��[���F�C�X�������Q�ש�����@�p�ɡC�̫�z���ש����}���ƪ��줽�ǵۤ�w�Ʃж��C�����L�Ф@���Ыȷh��G���СC�ڷP��ܩ_�ǡC�]���ھڧڦۤv���g��A�o�˪��հʥu��ťX�@�өж��Ӥw�A�M�ӥL�o���ݪťX�L���h�ж����o�Ǧh�ܵL�a�����l�a�C���ôb���uť��z���~��U�O�G
�u��G���ЫȦw�m��|���СA�T���ЫȨ줻���F�ӳo��h�An ���ЫȾE�� 2n ���СC�v
�{�b�ڤF�ѥL���p���F�G�o�p���O��L�a�h���_�ƩЪŤF�X�ӡA�N�i�H�w�y���l�a��_���СC
��O�Ҧ����Ʃг����ۦt�z�ʪ��Ǯa�A�_�ƩЫh�Ѷ��l�a�Ҧ��C�]�ڨS����ۤv�C�O�o�˪��F�g�L�T�Ѫ��{�ѡA�ڻP�t�z�ʪ��Ǯa�B�o�D�`�ͦn�A�L�̴N��ڬ��L�̾Ƿ|���a�A�N���F�]���ڤ]���ݻP�L�̦P�ɾE���C�ڥѤ@�ʸU�������ʸU���С^�C�ڦ��@�춰�l���B�ͱƦb����Ĥ��ʤC�Q�|��A�L�Q�s�J�@�d�@�ʥ|�Q�C���СC�@�뻡�ӡA�� n �춰�l�a�|�Q�s�� 2n-1 ���Ц��C
����Я�p�w�M�w�w�t�z�ʪ��ǾǷ|�����C�ʪ��Ǫ̳��_�{�^�a�A�ڤ]�h�츳�ƪ����J���ũЦ��C���O��ȫȦ��q���Ƥ����o�|�Ϻz�̰����A�X�Ѥ���ڨ��B�n���D�H�ܱo�ܼ~�{�C
�u������x���ܡH�v�ڰݥL�C
�u���b�Ʃж����ŵۡC�ڭ̱N�L�k�����g�٭p���C�v
�ƹ�W�ڨä��ӤF�ѥL�ҿת��g�٭p���F�רs�L�]����L�a�h�ж������O�C���ަp���A���٬O���L�@�ǫ�ij�G
�u�K�A������ȫȲ��ʤ@�U�A�ϥL�̺���ۦ��A�H�K��Ҧ��ж��������C�v
�o�ˬO����e����F�C���l�a�u���b�_�Ƹ��СG�@�B�T�B���B�C�B�E�����C���@���ЫȤ��ʡA��T���ЫȾE��G���A�����E��T���A�C���E��|�������C�̫�Y�ϨS���s�ȫȨ�ӡA�Ҧ����ж��S���s�Q�����C
���o�ä���������ƪ����~�T�G�ڻ��O���F�U�����Ƶo�T�F�y�`�̻\�F�t�z�j�����٤������A�ä��h�F���ؿv�ӤS�\�F�L�a�h�����]�A�C�@���]�S���L�a�h�ж��C���F�y�o�Ǯ��]�A�L�̧�n�h���Ȫe�t����A�H�ܩ�Ȫe�ڪ����Ũ���z�Z�A�o�i��ɭP�Y������G�C��O�L�̨��R���F�ڭ̪��j�����~�A��L���]������A�ç�ҥΪ������k�٭�B�C�����Ҧ������]�]�]�A�ڭ̪��^���Ⱥ��ɡA�n����o�D�R�O�O�������C���ƪ����R��L�a�h���]���ȫȦw�m��ڭ̳o�Ӧ��w�Ⱥ��������A�ӨC�@���]�S���L�a�h�ȫȡI
�u�ڤw�����F�I�v���ƪ��s�۵ۡC
�u�����ڦb���w�Ⱥ��������w���F�@�ӮȫȡA�M��O 999,999�A����Ʀܩ�O�L�a�h�ӮȫȡF�{�b�L�̤S�n�ڳ]�k���L�a�h�ӵL�a�h�ȫȦb�o����C���A�o�������O��ְ����F���L�̥h�w�Ƨa�I�v
���O�R�O�N�O�R�O�C�L�̥����b���Ѥ��dzƴN���A�H�K�e�Ƿs�ȫȡC�b�o���Ѥ������بS�H�u�@�ۢw�w�C�@�ӤH���b���ɸ��ķQ��k�ѨM�o���D�C��O�����ؤ��G�F�@���a��w�w�Y���H���ѸѨM��k�A�i�K�O�o��@�ӻȪe�t�Ȧ�C���Ҧ����X����k���]���i��Ӥ��Q�įǡC�Ҧp�@�ӥ��b���V�����p�v���@�p�U����ij�G���Ĥ@���Ъ��Ыȭ�a���ʡC��ĤG���E��@�d�s�@���СA�ĤT���E��ĤG�d�s�@�������A�M���ĤG���]���Ыȷh�J�G���A�@�d�s�G���A�G�d�s�G�������C�ĤT���]���h�J�T���C�@�d�s�T���A�G�d�s�T�������C���o��k�����įǡA�]���ӳo��k�A�h�Ĥ@�d�s�@�Ӯ��]���ȫȴN�����n�E�쨺��h�F���e�@�d�Ӯ��]���ȫȴN�e�ڤF�Ҧ����ж��C�o�ӿ�k���ڭ��p�Q�_�@��ơGù����ij������ij�N�E�몺�W�٧אּ���d�� (Tiberius)�A�H�ܹ�ӫҪ��q�N�]�e��Ӥ�w�ĥ� Julius �P Augustus ���ӫҪ��W�r�^�A�ӫҤ@ť�o��ij�A�H�f�N�ݰ�ij�����G�u����A�̮�����Ӫ��ܹ�ĤQ�T��ͼ����q�N�O�H�v
������ï�O�����@�Ӹ��n���ܳq��k�C�L��ij�ڭ̧Q�δX��żơA���s�w�ƮȫȦp�U�G�Ĥ@���]�]�Y�ڭ̳o�����^���ȫȦw�Ʀb�G���B�|���B�K���B�Q�����B�T�Q�G���ж������]�o�Ǹ��X�Φ����G���X��żơ^�C�ĤG���]���ȫȫh�w�m�b�T���B�E���B�G�Q�C���B�K�Q�@���ж������]�o�Ǧ����T���X��żơ^�C�L��ij�ڭ̧�Y�a���]���ȫȨ̦��k�w�ơC��O���ɭ��N�ݥL�G
�u�ڭ̬O�_��ĤT���]���ȫȦw�m�b���ǩж��C�Ϩ丹�X�Φ��H�|�����X��żơH�v
�u���M�A�vï�O���^���C
�u�o��k�]�ѨM���F���D�F�]���ڭ̤w��|���Ф����Ĥ@���]���@�ӮȫȡA�ڭ̤S�N��ĤT���]���Ĥ@��ȫȤ��쨺�̩O�H�v
��������ܤF�F�L�����ڦb�ӪždzN���c�Dzߤ��~���ƾDzש�S���նO�C
�u�ν�ơC��Ĥ@���]���ȫȦw�Ʀb�G���B�|���B�K���B�Q�����A�K�K�A�ĤG���]���b�T���B�E�B�G�Q�C���B�K�Q�@���A�K�K�A�ĤT���]���b�����B�G�Q�����B�@�ʤG�Q�����B���ʤG�Q�����A�K�K�A�ĥ|���]���b�C���B�|�Q�E���C�T�ʥ|�Q�T���A�K�K�A�v
�u�o�˴N���|�A�o�ͨ�ӮȫȳQ�w�Ʀb�P�@�өж����ƤF�ܡH�v���ɭ��ݡC
�u���|���A�]����ӽ�ƪ����賣���۵��F�]�N�O���A���p p, q ����Ӭ۲�����ơA�� m,n ����Ӧ۵M�ơA�h 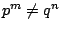 �C�v �C�v
���ɭ��P�N�ڪ����k�C���ܧ֪��L��i�F�کҴ�����k�ӥu�� 2, 3 ��ӽ�ơC�L��ij��� m �Ӯ��]���� n �ӮȫȦw�Ʀb 2m 3n ���ж��C�o�Ӥ�k��o�q�A�]�����p 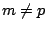 �� �� 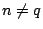 �A6 �h �A6 �h
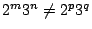 �C��O�N���|����ӮȫȳQ�w�Ʀb�P�@�ж��F�C �C��O�N���|����ӮȫȳQ�w�Ʀb�P�@�ж��F�C
�C�ӤH�����N�o�ӫ�ij�C�j�a���H���L�k��쪺���D�ש�o��F�ѵ��C���X�G�N�ƪ��A���ɭ��P�ڳ��S�o�����C�]�����p�ھڧڭ̪���k�A�h���Ӧh���ж��N�O�Ū��]�ھڧڪ���k�A�h�����B�Q���B�Q�G���H�ΩҦ����O�Y�@��ƪ����誺�ж����S�H���A�ӫ��ɭ�����k�h�ϩҦ����X���O 2m 3n �Φ����ж��ŵۡ^�C���@�춰�l�a��ij�@�ӳ̦n����k�C�o�춰�l�a�O���Z�Ȫe�t�ƾǬ�s�|�|���C
�L��ij�ڭ̦C���C����]�����ƨ̦��Ʀb�C�W�A�өЫȪ����ƫh�Ʀb��W�C�Ҧp�ĥ|�C�Ĥ���W�ұƪ��O�ĥ|���]���Ĥ��Ыȸ��ơC�U���N�O�o�Ӫ��]���u�C�F���W���������A�]���Y�n�����C���A�h�ݥεL���h����M�C�^�G
�u�M���ȫȨ̥���Φw�ơA�v���l�ƾǮa���C
�u�p��w�ơH�v���ɭ��ä��F�ѥL������k�C
�u�Υ���ΡC�Ҧp��@���Цw�Ƶ� (1,1) �ȫȡA�]�N�O�Ĥ@���]���Ĥ@�ȫȡF�G���е� (1,2) �ȫȡA�N�O�Ĥ@���]���ĤG�ȫȡF�T���е� (2,2) �ȫȡA�Y�ĤG���]���ĤG�ȫȡA�ӥ|���Ыh�� (2,1) �ȫȡA�Y�ĤG���]���Ĥ@�ȫȡC��O���W��������G������ΤW���ȫȳ��w�Ƨ����C�M��~�� (1,3) ���Ʀb�����СA(2,3) ���Ʀb�����СA(3,3) ���Ʀb�C���СA(3,2) ���Ʀb�K���СA(3,1) �h�Ʀb�E���С]�o�ǩж��ƺ��F����� 3 ������ΤW���ȫȡC�^�]�N�O�̤U�����b�Y��V�w�ơG
�u�u���������ж����Ҧ����ȫȶܡH�v���ɭ����h�ê��ݡC
�u���M�o�C�ھڳo�ӳ]�p�A�h�e n �Ӯ��]���e n �өж��C��O�C�@�ȫȦ��߷|����@�өж��C�|�һ��A�Ĥ@�ʤT�Q�����]���ĤG�ʤQ�C���Ыȷ|�b�ĤG�ʤQ�C�������o������ж��C�ڭ̬Ʀܥi�H�ܮe������X�L�ұo�쪺�ж����X�C���O�� 2162 + 136 ���СC�@�뱡�ΡA�� m �Ӯ��]���� n �ӮȫȡA�Y 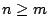 �ɫh����� (n-1)2 + m ���СA�Y n<m �h����� m2-n+1 ���СC�v �ɫh����� (n-1)2 + m ���СA�Y n<m �h����� m2-n+1 ���СC�v
�o�ӳ]�p�Q���{���̦n���w�w�Ҧ����]���ȫȦb�ڭ̪��������|���ж����A�P�ɳo�����]���|���ũСC��O�o�춰�l�ƾǮa�o��F����C�L�M�w�� LCR-287 �Ȫe�t�h�Ȧ�C���ɭ��]�b�y���o�Ӧ��\���ѨM��k�C�Ҧ��ȫȳ��Q�ܰѥ[�b�|�C�D�H�w�ƨC�ӤH�@�ӧ���C�����Ƹ����ЫȦ]���b�p�ɦӧ䤣���m���A��O�L�̱o���j�a�⧤��վ��~��J�y�]���M���t�[�Ȥl�^�C��ӷ��B�N�O�W��ɡA�o�o�{�C�H������B�N�O�C�ƹ�W�p�l�u�dzƨC�H�@���F�ڧƱ�Ū�̲{�b�ӷ|�F�ѳo�쩳�O���@�^�ƤF�C
�b�|����A�ڧ��W�ڪ����l���b�A�_�{�^�a�y�C�ڥ����i�D�a�y�W���Ѥ�Ǯa�A�t�z���s�s�b������C�������~�A���٭n�бФ@�Ǧ��W�檺�ƾǮa�M�ڪ��B�ͤj����б¡A�����L�����X���ʽ�C
|