二、平行性與定量平面幾何基礎理論 (第 4 頁)

　1│2│3│4│5　

《基礎幾何學》

二、平行性與定量平面幾何基礎理論（第 4 頁）

項武義

首頁 | 搜尋

．作者任教於香港科技大學數學系
‧對外搜尋關鍵字

不可公度性的發現與克服——Hippasus 和 Eudoxus 對于人類理性文明的重大貢獻

話說當年，畢氏的門徒 Hippasus 對于當年定量幾何學的頭號公設，亦即「直線段之間可公度性普遍成立」還一直在鍥而不捨地鑽研。在當年，至少他已認識到下述兩個給定的可公度線段 a, b 的最長公尺度的幾何求法：

【輾轉丈量法】：設 a<b，我們用 a 為尺去丈量 b 。若恰能整量，即 b=n₁a，則顯然 a 本身就是 {a,b} 的最長公尺度。不然， b=n₁a+r₁, r₁<a 。再用 r₁ 為尺丈量 a 。若恰能整量，則 r₁ 即為 {a,b} 的最長公尺度。不然， a=n₂r₁+r₂ 。再用 r₂ 為尺丈量 r₁，如此輾轉丈量，一直到 r_k 恰能整量 r_k-1 為止。則 r_k 即為所求的最長公尺度。

【歷史的註記】：在 {a,b} 可公度的情形，即有 a=mc, b=nc 。相應于 {a,b} 的輾轉丈量，即有 {m,n} 的輾轉相除求最大公因數的算法，而在 $r_{k}=d\cdot c$ 式當中，d 就是 m, n 的最大公因數。因為這種輾轉相除算法寫在歐幾里得的 ``Elements'' 中，所以通常稱之為歐氏算法 (Euclidean Algorithm) 。但是在古希臘極可能是先有輾轉丈量求最長公尺度，因為這是當年學者們鑽研的定量幾何基本問題。總之由其一自然也就可直接對應而有其另一。所以歐氏算法顯然在歐氏的 ``Elements'' 之前二百年即已為 Hippasus 所知和所用。話說當年，Hippasus 在沙盤上用蘆葦杆畫了一個大致如 [圖 2-10] 所示的正五邊形，然後開始用當時業已熟知的等腰三角形定理和三角形內角和定理來作下述分析，即 (i) 三角形內角和恆等于 π（平角）；和 (ii) 等腰三角形的兩底角相等，反之，兩底角相等的三角形必為等腰。

$\begin{displaymath} \begin{xy} \xyimport(5,5){\epsfxsize =8cm \epsfbox{fig0210.e... ...1,3.57)*+{\frac{\pi}{5}} ,(3.01,1.47)*+{\frac{\pi}{5}} \end{xy}\end{displaymath}$

[ 圖 2-10 ]

五邊形的內角和恆等于 $3\pi$ ，所以上述正五邊形 $\hskip-3pt\raise-1pt\hbox{ \xy\xyimport(1,1){\epsfxsize=0.4cm\epsfbox{pentagon.eps}}*\frm{} \endxy }A_{1}B_{1}B_{2}C_{2}C_{1}$ 的每個內角都等于 $\frac{3\pi}{5}$ 。由此可見等腰三角形 $\bigtriangleup B_{1}B_{2}C_{2}$ 和 $\bigtriangleup B_{2}C_{2}C_{1}$ 的兩底角皆為 $\frac{\pi}{5}$ 。令對角線 $\overline{B_{1}C_{2}}$ 和 $\overline{B_{2}C_{1}}$ 的交點為 A₂，則有 $\bigtriangleup C_{1}A_{2}C_{2}$ 的兩底角皆為 $\frac{2\pi}{5}$ ，而 $\bigtriangleup A_{2}B_{2}C_{2}$ 的兩底角皆為 $\frac{\pi}{5}$ ，所以它們都是等腰的。

上述看來不起眼的幾何分析卻使得 Hippasus 大為震驚！為什麼呢？若以上述五邊形的邊長 a 去丈量其對角線長 b，則其餘段 r₁ 就是等腰 $\bigtriangleup A_{2}B_{2}C_{2}$ 的等邊邊長。若將 $\overline{C_{1}C_{2}}$ 延長一段 $\overline{C_{2}C_{3}}=r_{1}$ ， $\overline{B_{1}B_{2}}$ 延長一段 $\overline{B_{2}B_{3}}=r_{1}$ ，則易証 $\hskip-3pt\raise-1pt\hbox{ \xy\xyimport(1,1){\epsfxsize=0.4cm\epsfbox{pentagon.eps}}*\frm{} \endxy }A_{2}B_{2}B_{3}C_{3}C_{2}$ 又是一個正五邊形，而它的邊長是 r₁，對角線長則是 a 。

因此當我們再用 r₁ 去丈量 a 時，在本質上又是用一個正五邊形的邊長去丈量其對角線長。同理，所得的餘段 r₂ 又是一個更小一號的正五邊形的邊長而其對角線長則為 r₁ 。如此輾轉丈量，每一次所做者在本質上總是用一個正五邊形的邊長去丈量其對角線長，只是那個正五邊形逐次縮小吧了。這樣就理論上証明了 {a,b} 的輾轉丈量必然是永無止休的！因此 {a,b} 必然是不可公度的 (non-commensurable)！此事焉能叫他不吃驚!?這個驚人的發現事實勝于雄辯地証明了當年定量幾何基礎論的頭號基石——「可公度性的普遍成立」其實根本是一個錯誤的「公設」！

Hippasus 接著還用下述圖解証明正方形的邊長和對角線長 {a',b'} 之間的輾轉丈量也是永無止休的，所以也是不可公度的。

$\begin{displaymath} \begin{xy} \xyimport(5,5){\epsfxsize =3.5cm \epsfbox{fig0211... ...(4.35,1.05)*+{r_1} ,(2.7,2.75)*+{b'} ,(5.25,2.7)*+{a'} \end{xy}\end{displaymath}$

[ 圖 2-11 ]

由 [圖 2-11] 可以看出 {a',b'} 的輾轉丈量所得的逐步算式是

$\begin{displaymath}\begin{array}{rcl} b' &=& a'+r_{1}\\ a' &=& 2r_{1}+r_{2}\\ ... ...selectfont \cH237}}}\\ r_{k-1} &=& 2r_{k}+r_{k+1} \end{array} \end{displaymath}$

所以是永無止休的。[細節的証明留作習題]

【歷史的註記】：Hippasus 的偉大發現，是人類理性文明的重要里程碑，有如發現了一個理念上的新大陸，它不單對于定量幾何學有根本的重要性，其實對于整個自然科學都有深遠的影響。但是當年古希臘幾何學界，特別是 Hippasus 本人所在的畢氏學派對于這個偉大發現的反應，卻是全然無理性的。據某些現在已不可詳考的記載，Hippasus 反而因為這個重大發現而喪生于同門之手。

其實，不可公度性的存在，並不是全面否定了當年古希臘幾何學在定量幾何基礎論上的成就。它只是說原本以為已經完整無缺的証明其實只是在可公度的情形的証明，而在一般不可公度的情形，則尚有待補証！這個亟待補証的任務對于當年整個古希臘幾何學界是一個嚴峻而且迫切的挑戰。大約經歷半個世紀的努力，才促使 Eudoxus 開創了影響無比深遠廣闊的逼近法和逼近原理而得以完美成功。可以這麼說，Eudoxus 的思想和方法提供了研討和理解 Hippasus 所發現的新大陸的基礎。

Eudoxus 的逼近法和逼近原理(Method and Eudoxus principle of approximation)：

當 {a,b} 不可公度時，「a:b」不是一個分數。它是一種有待理解的新興事物，不管你如何稱呼它，反正是一種當時尚未瞭解有待研究的「新量」。例如 {a,b} 和 {a',b'} 是兩對不可公度的直線段，Eudoxus 認識到「a:b」和「a':b'」這兩個「新量」之間的大小或相等關係都還有待定義！但是當 {a,b} 不可公度而 {a',b'} 可公度的情形下：

$\begin{displaymath}a:b \; \hbox{ {\fontfamily{cwM0}\fontseries{m}\selectfont \cH184} }\; a':b'=\frac{m}{n}\end{displaymath}$

它們之間的大小關係卻又是相當清楚的，亦即：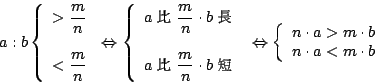

$\begin{displaymath}a:b \left\{ \begin{array}{l} \displaystyle > \frac{m}{n} \\ ... ...n\cdot a > m\cdot b \\ n\cdot a < m\cdot b \end{array} \right. \end{displaymath}$

這也就是 Eudoxus 在研究這種「新量」時第一個認識到的：

Eudoxus 比較原則：

$\begin{displaymath}a:b \left\{ \begin{array}{l} \displaystyle > \frac{m}{n} \\ ... ...n\cdot a > m\cdot b \\ n\cdot a < m\cdot b \end{array} \right. \end{displaymath}$

亦即 a:b 和 $\frac{m}{n}$ 的比較大小可以由 $n\cdot a$ 和 $m\cdot b$ 之間的比較長短而判定之。而後者是極為初等而且其幾何意義乃是一目瞭然的。

在 {a:b} 和 {a':b'} 都是不可公度的情形，若有分數 $\frac{m}{n}$ 使得

$\begin{displaymath}a:b>\frac{m}{n}>a':b' \quad \hbox{{\fontfamily{cwM0}\fontseri... ...na'<mb'\hbox{{\fontfamily{cwM0}\fontseries{m}\selectfont \cH4}}\end{displaymath}$

則顯然應該定義前者大于後者。反之，若有分數 $\frac{m}{n}$ 使得 $a:b<\frac{m}{n}<a':b'$ ，則應該定義前者小于後者。

再者，假如這種間于 a:b 和 a':b' 之間的分數是不存在的情形，亦即對于任何分數 $\frac{m}{n}$ , a:b 和 a':b' 與 $\frac{m}{n}$ 之間的大小關係總是同步同樣的，理當就可以作為「a:b=a':b'」的定義。

這也就是 Eudoxus 當年對于兩個不可公度的比值之間的大、小及相等關係的定義，即

【定義】：

a:b>a':b' $\Leftrightarrow$ 存在分數 $\displaystyle %% \frac{m}{n}$ 使得 $a:b>\displaystyle \frac{m}{n}>a':b'$

a:b<a':b' $\Leftrightarrow$ 存在分數 $\displaystyle %% \frac{m}{n}$ 使得 $a:b<\displaystyle \frac{m}{n}<a':b'$

a:b=a':b' $\Leftrightarrow$ 對于任何分數 $\displaystyle \frac{m}{n}$ 皆有相同的大小關係。

亦即：

$\begin{displaymath} na \left\{ \begin{array}{c} > \\ < \end{array}\right\} mb \... ...w na' \left\{ \begin{array}{c} > \\ < \end{array}\right\} mb' \end{displaymath}$

為了論証上述定義的必然性，Eudoxus 開創了影響極為深遠的逼近法) (Method of Approximation) 。首先，他提出下述直觀上極為明顯的「公設」作為其論証的依據：

任給兩個直線段 a,b，不論前者有多短而後者有多長，總有足夠大的整數 N 使得 $N\cdot a$ 比 b 長。

【定理】：設 {a,b} 是不可公度者，對于任給正整數 n，恆存在 m 使得

$\begin{displaymath}\frac{m}{n}<a:b<\frac{m+1}{n}\end{displaymath}$

証明：由上述公設，必有足夠大的 N 使得 $\frac{1}{n} b$ 的 N 倍要比 a 長。令 m+1 為這種 N 之中的最小者，則有

$\begin{displaymath}m(\frac{1}{n}b)<a<(m+1)(\frac{1}{n}b)\end{displaymath}$

亦即

$\begin{displaymath}\frac{m}{n}<a:b<\frac{m+1}{n} \eqno \Box \end{displaymath}$

[註]：因為 n 是可以任意大的，所以上述左、右夾逼 a:b 的兩個分數之間的差額 $\frac{1}{n}$ 是可以小到任意小的。[用現代的術語，即對于任給正數 $\varepsilon >0$ ，皆有足夠大的 n 使得 $\frac{1}{n} < \varepsilon$ 。] 所以 a:b 和 $\frac{m}{n}$ 或 $\frac{m+1}{n}$ 之間的差別當然也可以小到任意小。基于上述定理，就可以進一步說明前述不可公度的「比值」之間大、小、相等關係的定義的必然性：

設 a:b 和 a':b' 對于任給分數恆具有相同的大小關係，則對于任給 n，都有相應的 m，使得

$\begin{displaymath}\frac{m}{n}<a:b\, ,\; a':b'<\frac{m+1}{n}\end{displaymath}$

因此 a:b 和 a':b' 之間的差別要比所有 $\frac{1}{n}$ 都小。不論上述差別是那一種新量，它是一個固定的量而它又比所有 $\frac{1}{n}$ 都小，所以唯一的可能者就是零，亦即 a:b=a':b' 。再者，在 a:b 和 a':b' 不等的情形，則有一個分數，它和兩者的大小關係是不同的，這也就是前述比較大小的定義。

有了上述思想和逼近法，再進而重建當年希臘的定量幾何學，乃是順理成章之事，其要點在于原先僅僅對于可公度的情形具有証明的各種各樣定理和公式，作出其在不可公度的情形的「補証」。例如下述矩形公式：

$\begin{displaymath}\square (a,b):\square(u,u)=(a:u)(b:u)\end{displaymath}$

在 a:u 和 b:u 都是分數時業已証明，而在 a:u 和 b:u 至少有一個不是分數（亦即不可公度）時，需要補証。

Eudoxus 對于上述矩形面積公式所作的補証，大致如下：

對于任給正整數 n ，不論它有多大，皆有 m 和 m' 使得

$\begin{displaymath}\frac{m}{n}<a:u<\frac{m+1}{n},\; \frac{m'}{n}<b:u<\frac{m'+1}{n}\end{displaymath}$

亦即

$\begin{displaymath}\frac{m}{n}u<a<\frac{m+1}{n}u,\; \frac{m'}{n}u<b<\frac{m'+1}{n}u\end{displaymath}$

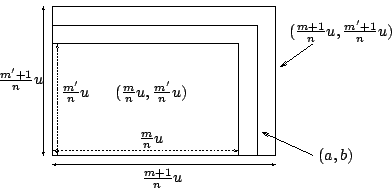
$\begin{displaymath} \begin{xy} \xyimport(5,5){\epsfxsize =6cm \epsfbox{fig0212.e... ... ,(5.5,4.2)*+{\square(\frac{m+1}{n}u,\frac{m'+1}{n}u)} \end{xy}\end{displaymath}$

[ 圖 2-12 ]

如 [圖 2-12] 所示， $\square (a,b)$ 包含 $\square(\frac{m}{n}u, \frac{m'}{n}{u})$ ，而且它又包含于 $\square(\frac{m+1}{n}u, \frac{m'+1}{n}{u})$ 之中，由此可得

$\begin{displaymath}\frac{mm'}{n^{2}}<\square(a,b):\square(u,u)<\frac{(m+1)(m'+1)}{n^{2}}.\end{displaymath}$

再者，由前述不等式的相乘，亦有

$\begin{displaymath}\frac{mm'}{n^{2}}<(a:u)(b:u)<\frac{(m+1)(m'+1)}{n^{2}}\end{displaymath}$

因此， $\square(a,b):\square(u,u)$ 和 (a:u)(b:u) 之間的差別（假如有的話）必然要比同時左、右夾逼兩者的兩個分數之間的差別要更小，即小于

$\begin{displaymath}\frac{(m+1)(m'+1)}{n^{2}}-\frac{mm'}{n^{2}}=\frac{m+m'+1}{n^{2}}%% =\frac{1}{n}\bigg(\frac{m}{n}+\frac{m'+1}{n}\bigg)\end{displaymath}$

在 n 無限增大時，它是可以小到任意小的。所以 $\square(a,b):\square(u,u)$ 和 (a:u)(b:u) 之間不可能有任何差別，亦即所要補証的矩形面積公式

$\begin{displaymath}\square (a,b):\square (u,u) = (a:u)(b:u) \eqno \Box \end{displaymath}$

長話短說，Eudoxus 所創的逼近法不但把當年僅僅在可公度的特殊情形下具有其証明的各種各樣定理和公式，加以明確簡潔的「補証」，使得它們不論在可公度或不可公度的情形皆普遍成立，從而徹底重建了定量幾何基礎論。再者，他有鑒于曾經採用錯誤的「公設」作為幾何學的論証依據的慘痛教訓，決心下功夫徹底檢查當代的幾何學，盡其所知所能把其論証的依據，精簡壓縮到「至精至簡」；流傳至今的《歐氏幾何學》 (Euclidean Geometry) 其中絕大部分來自 Eudoxus 的著作。所以「公理化」治學的典範和人類理性文明中的第一科學的初階集其大成，實乃 Eudoxus（而並非 Euclid）的偉大貢獻。不但此也，Eudoxus 的逼近原理和方法論不但重建了定量幾何基礎論，而且也是分析學 (Analysis) 的發祥地和基本方法。他本人就把它用來証明錐體體積等于三分之一底面積乘高這個立體幾何基本公式，他的証法以及隨後 Archimedes 把它拓展到球面面積公式和球體體積公式的論証乃是積分學的雛形和範例。

如今回顧反思，將中、西古文明的定量平面幾何作一比較分析：兩者所得的基本公式大致相同，亦即矩形、三角形的面積公式，勾股弦公式（亦即畢氏定理）和相似三角形的邊長比例式，但是在基調和格局上則兩者是迥然不同的。中國古代的工程師研討幾何是為了致用，是唯用是尚的；他們在基本測量公式的推導上善用面積，的確有其獨到的長處，但是在對于空間本質理解的深度上，比之于古希臘幾何學是的確膛乎其後的了。究其原因，相信並非是在聰明才智上有任何差別，而是在格調、志趣和氣概上有所分野！例如「可公度性」乃是一個純理論性的問題；在實用的度量中，在力所能及的準確度之下的微量根本沒有其實質意義，所以不存在可不可公度這種問題。由此可見，在唯用是尚的格局下，根本是不會有此一問的，當然也不會有 Hippasus 這種深深觸及空間的連續性的發現和歷經半世紀的奮鬥才結晶而得出的 Eudoxus 逼近原理和方法論，是不？由此反思，同學們應該體認到局限中國古代幾何的發展因素乃是：「唯用是尚，則難見精深，所及不遠」；而古希臘幾何學上的成功給全人類的啟示與鼓舞則是：「若以理解大自然為志趣，並能世代相承、精益求精，則宇宙基本結構的至精至簡、至善至美是可望可及的」。

　1│2│3│4│5　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

最後修改日期：6/19/2004