Lagrange 乘數法

Lagrange Multiplier Method

Lagrange（拉格朗日，1736～1813）18世紀最偉大的數學家之二，另一位是長他29歲的 Euler（尤拉，1707～1783）。Euler 賞識 Lagrange，在1766年和 d'Alembert 一起推薦 Lagrange 為（柏林科學院）Euler 的繼承人。

在他一生浩瀚的工作中，最為所有數學家熟知的發明就是 Lagrange multiplier（拉格朗日乘數）或 Lagrange multiplier method，這是一個求極值的方法。比方在兩個變數的時候，我們要找 f(x,y) 的極值，一個必要的條件是：

$\begin{displaymath} \frac{\partial f}{\partial x}=\frac{\partial f}{\partial y}=0 \end{displaymath}$

但是如果 x,y 的範圍一開始就被另一個函數 g(x,y)=0 所限制，Lagrange 提出以 $f(x,y)+\lambda g(x,y)$ 對 x 和 y 的偏導數為 0，來代替 $\frac{\partial f}{\partial x}=\frac{\partial f}{\partial y}=0$ 作為在 g(x,y)=0 上面尋找 f(x,y) 極值的條件。式中引入的 λ 是一個待定的數，稱為乘數，因為是乘在 g 的前面而得名。

首先我們注意，要解的是 x,y 和 λ 三個變數，而

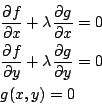
$\begin{eqnarray*} &&\frac{\partial f}{\partial x}+\lambda\frac{\partial g}{\part... ...partial y}+\lambda\frac{\partial g}{\partial y}=0 \\ &&g(x,y)=0 \end{eqnarray*}$

雖然有三個方程式，原則上是可以解得出來的。

以 f(x,y)=x， g(x,y)=x²+y²-1 為例，當 x,y 被限制在 x²+y²-1=0 上活動時，對下面三個方程式求解

$\begin{eqnarray*} &&\frac{\partial}{\partial x}[x+\lambda(x^2+y^2-1)]=1+2\lambda... ...l}{\partial y}[x+\lambda(x^2+y^2-1)]=2\lambda y\\ &&x^2+y^2-1=0 \end{eqnarray*}$

答案有兩組，分別是 x=1，y=0， $\lambda=-\frac{1}{2}$ 和 x=-1，y=0， $\lambda=\frac{1}{2}$ 。對應的是 x²+y²-1=0 這個圓的左、右兩個端點。它們的 x 坐標分別是 1和 -1，一個是最大可能，另一個是最小可能。

讀者可能認為為何不把 x²+y²-1=0 這個限制改寫為 $x=\cos\theta$ 、 $y=\sin\theta$ 來代入得到 $f(x,y)=f(\cos\theta ,\sin\theta)$ ，然後令對 θ 的微分等於 0 來求解呢？對以上的這個例子而言，當然是可以的，但是如果 g(x,y) 是相當一般的形式，而無法以 x,y 的參數式代入滿足，或是再更多變數加上更多限制的時候，舊的代參數式方法通常是失效的 ^註1 。

這個方法的意義為何？原來在 g(x,y)=0 的時候，不妨把 y 想成是 x 的隱函數，而有 g(x,y(x))=0，並且 f(x,y) 也變成了 f(x,y(x))。令 $\frac{d}{dx}f(x,y(x))=0$ 根據連鎖法則，我們得到

$\begin{displaymath} f_x+f_y\frac{dy}{dx}=0 \end{displaymath}$

和（因為 $\frac{d}{dx} g(x,y(x))$ 恆等於 0）

$\begin{displaymath} g_x+g_y\frac{dy}{dx}=0 \end{displaymath}$

因此有行列式為 0 的結論。

$\begin{displaymath} \left\vert \begin{array}{cc} f_x&f_y\\ g_x&g_y \end{array}\right\vert =0 \end{displaymath}$

這表示 f_x,f_y 和 g_x,g_y 成比例，所以有 λ ^註2

$\begin{displaymath} \begin{array}{lll} f_x&=&\lambda g_x\\ f_y&=&\lambda g_y \end{array}\end{displaymath}$

另外一個解釋是幾何圖形的角度來考量。我們考慮 f(x,y) 的等位曲線，亦即 f(x,y)=c 諸曲線，如果曲線 f(x,y)=c 與 g(x,y)=0 互相穿過，亦即如果互不相切，則 f(x,y) 稍稍大於 c（或稍稍小於 c）都會持續穿過 g(x,y)=0，這就表示在 g(x,y)=0 之上，c 不可能是一個極值，反過來說，如果 c 是極值的話，f(x,y)=c 這條曲線和 g(x,y)=0 一定互相切著，會有相同的切線，也可以說有相同的法線。但是 f(x,y)=c 和 g(x,y)=0 的法線方向分別是 $(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})$ 和 $(\frac{\partial g}{\partial x},\frac{\partial g}{\partial y})$ ，它們必須平行，因此

$\begin{displaymath} (\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}... ... (\frac{\partial g}{\partial x},\frac{\partial g}{\partial y}) \end{displaymath}$

λ 待定。從這裡也可以看出萬一 $(\frac{\partial g}{\partial x},\frac{\partial g}{\partial y})=(0,0)$ 那 λ 多半是求不出來的。然而 $(\frac{\partial g}{\partial x},\frac{\partial g}{\partial y})\neq (0,0)$ 恰好保證了 y 是 x 或 x 是 y 的隱函數，這又回到了上一段以隱函數為出發點來解釋乘數法的前提。

乘數法有許多用處，舉凡在若干限制條件之下求極值的問題，都可以考慮引用這個方法。當然如前所述，引用本法雖然有若干限制，這些限制反映了問題本身的特質，本來就是問題的一部分，值得好好推敲。

Lagrange 一生貢獻無數，Boyer ^註3 讚美他是

... the keenest mathematician of the eighteenth century ...
（十八世紀最敏銳的數學家）

他所發明的乘數法展現了他對這類問題敏銳的洞察力。這正是 "keenest" 最佳的詮釋。

對外搜尋關鍵字：
．Euler
．d'Alembert
．等位曲線

（撰稿：張海潮∕台大數學系）


	留言（若有指正、疑問……可利用這裡留言）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：李渭天

最後修改日期：9/4/2001