群論的起源

．原載於科學月刊第十七卷第七期
．作者當時任教於台灣大學數學系

群論的起源

曹亮吉

「群」這個觀念在數學及自然科學中都非常重要，而它的起源則是為了解方程式。

一次、二次方程式的解法很早就為人所熟悉。高次方程式的解法有兩個方向。其一為數字係數方程式的數值近似解，這種方法最早在中國發展得很完善。另一種則為文字係數方程式的根式解，它在十六世紀上半因義大利一些數學家解決了三次及四次的問題，而掀起了高潮。

一般的三次方程式都可以經由移根的處理，而變成x³+px+q=0。若以ω表1約三次方根 $\frac{(-1+\sqrt{-3})}{2}$ ，則此方程式的三根為

$\begin{displaymath}x_1=u+v,x_2=u\omega +v\omega ^2,x_3=u\omega ^2+v\omega \end{displaymath}$

其中

$\begin{displaymath}u=\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}} \quad v=\sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}\end{displaymath}$

這些公式都是由係數經四則運算及開方運算表示出來的，所以說三次方程式有根式解四次方程式一樣有根式解，雖然其公式比三次的要複雜得多。

當三次及四次方程式獲解後，大家的注意力自然就轉到五次方程式。在這方面，雖然經過十七、十八兩世紀的努力，但幾乎都交了白卷。直到十八世紀末的Lagrange (1736-1813年)，才算有些突破。他經由方程式根的置換觀點，把四次以下的方程式給予統一的解法。

先以三次方程式為例。令

$\begin{array}{rcl} y_1 & = & \frac{(x_1+\omega x_2+\omega ^2x_3)}{3}\\ y_2 & = ... ...3}\\ y_6 & = & \omega ^2y_4=\frac{(\omega ^2x_1+\omega x_2+x_3)}{3} \end{array}$

考慮

$\begin{displaymath} f(y)=\prod ^6_{i=1} (y-y_i) \end{displaymath}$

則
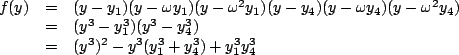
$\begin{array}{rcl} f(y) & = & (y-y_1)(y-\omega y_1)(y-\omega ^2y_1)(y-y_4)(y-\om... ...(y^3-y_1^3)(y^3-y^3_4)\\ & = & (y^3)^2-y^3(y_1^3+y_4^3)+y_1^3y_4^3 \end{array}$
將(x₁,x₂,x₃)的順序重排，就稱為x_i的一個置換，譬如(x₁,x₂,x₃) 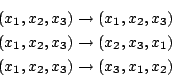$\rightarrow$ (x₃,x₁,x₂)就是一個置換。而在x_i的置換之下，y₁變成了y₂，y₂變成了y₃，而y₃變成了y₁，因此我們得到y₁，y₂， y₃的一個置換(y₁,y₂,y₃) $\rightarrow$ (y₂,y₃,y₁)。同理，x_i的置換(x₁,x₂,x₃) $\rightarrow$ (x₃,x₁,x₂)也引起y₄, y₅,y₆的一個置換 (y₄,y₅,y₆) $\rightarrow$ (y₅,y₆,y₄)。x_i的置換一共有6個，它們把y₁分別變到y_i。這6個置換中有三個

$\begin{eqnarray*} &(x_1,x_2,x_3)\rightarrow(x_1,x_2,x_3)\\ &(x_1,x_2,x_3)\rightarrow(x_2,x_3,x_1)\\ &(x_1,x_2,x_3)\rightarrow(x_3,x_1,x_2) \end{eqnarray*}$

引起y₁，y₂，y₃間的置換，使y₁³=y₁y₂y₃不變;也引起y₄,y₅,y₆間的置換，因比也使 y₄³=y₄y₅y₆不變。但另外三個x_i的置換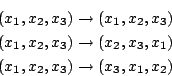

$\begin{eqnarray*} &(x_1,x_2,x_3)\rightarrow(x_1,x_3,x_2)\\ &(x_1,x_2,x_3)\rightarrow(x_2,x_1,x_3)\\ &(x_1,x_2,x_3)\rightarrow(x_3,x_2,x_1) \end{eqnarray*}$

則使y₁,y₂,y₃與y₄,y₅,y₆兩者之間互變。這就說明了x_i無論怎麼置換， f(y)的係數y₁³+y₄³及y₁³y₄³總是不變，所以它們是x_i的對稱式，因此可以寫成為原方程式係數的有理式。經計算可得

$\begin{eqnarray*} y_1^3+y_4^3&=-q\\ y_1^3y_4^3&=-\frac{p^3}{27} \end{eqnarray*}$

f(y)是y³的二次式，稱為原方程式的預解式，因為由f(y)=0，我們可以解得y₁³及y₄³，再從y₁、y₄(它們正是前面所提到的u及v)及 $0=\frac{(x_1+x_2+x_3)}{3}$ ，就可以得到三根的公式。

這種利用根置換求得根式解的方法可以用到四次方程式。解四次方程式時，若令 $y_1=\frac{(x_1+ix_2-x_3-ix_4)}{4}$ ， $i=\sqrt{-1}$ 為1的四次方根，則x_i的24個置換，會把y₁變成y_i， $1\leq i \leq 24$ 。這24個y_i分成六組，每組10個，組員之間所差的是i的倍數，譬如y₁，y₂=iy₁，y₃=iy₂，y₄=iy₃為一組。組員的乘積，譬如 y₁y₂y₃y₄=y₁⁴，為預解式的一根。可惜這樣的預解式為六次，所以行不通。

然而y₁的選擇並不是那麼死板。我們可以試x_i的任何有理式。若令 y₁=x₂x₃+x₁x₄，則x_i的24個置換只能使y₁變成y₁， y₂=x₁x₃+x₂x₄或 y₃=x₁x₂+x₃x₄，而任何一個x_i的置換一定引起y_i的置換。所以

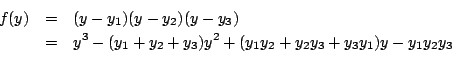
$\begin{eqnarray*} f(y) & = & (y-y_1)(y-y_2)(y-y_3)\\ & = & y^3-(y_1+y_2+y_3)y^2+(y_1y_2+y_2y_3+y_3y_1)y-y_1y_2y_3\\ \end{eqnarray*}$

的係數在x_i的置換之下是不變的，因此是原來四次方程式 x⁴+ax³+bx²+cx+d=0的係數的有理式。由計算可得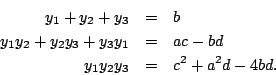

$\begin{eqnarray*} y_1+y_2+y_3&=&b\\ y_1y_2+y_2y_3+y_3y_1&=&ac-bd\\ y_1y_2y_3&=&c^2+a^2d-4bd. \end{eqnarray*}$

如此，我們就可以解出預解式f(y)=0的三個根y₁,y₂，y₃。因 y₁=x₂x₃+x₁x₄及 x₁x₂x₃x₄=d為已知，所以x₂x₃，x₁x₄可解。又由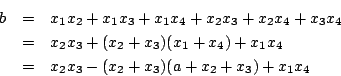

$\begin{eqnarray*} b &=& x_1x_2+x_1x_3+x_1x_4+x_2x_3+x_2x_4+x_3x_4 \\ &=& x_2x_... ...x_3)(x_1+x_4)+x_1x_4 \\ &=& x_2x_3-(x_2+x_3)(a+x_2+x_3)+x_1x_4 \end{eqnarray*}$

我們得到x₂+x₃的二次式，所以x₂+x₃可解。最後從x₂+x₃及x₂x₃可解得x₂。其他根的求法類似。

Lagrange成功地用根的置換觀點，解了三次及四次方程式後，自然用同樣的方法試著去解五次方程式。為了進一步了解這種嘗試，我們用濃縮的表示法來代替所談的置換。譬如 $(x_1,x_2,x_3)\rightarrow (x_3,x_1,x_2)$ 表示根是依 $x_1 \rightarrow x_3 \rightarrow x_2 \rightarrow x_1$ ，這種方式置換的，就以(1,3,2)表之。如果置換為 $(x_1,x_2,x_3)\rightarrow (x_2,x_1,x_3)$ ，則以(l，2)(3)表之，而簡寫為(1,2)。如果置換為 $(x_1,x_2,x_3)\rightarrow (x_1,x_2,x_3)$ ，則以(1)代替(1)(2)(3)來表示。請注意:括號內的數字是環狀排列的，因此 (10xA14130xA1412)=(3,2,1)=(2,1,3)。

三個根的置換一共有6個:(1),(1,2),(2,3),(1,3),(1,2,3),(1,3,2)。它們之間可以做合成的運算。譬如先做置換(1,2)，再做置換(1,3,2)，則x₁先變成x₂，再變成x₁，x₂先變成x₁，再變成x₃，而x₃先是不動，再變成x₂所以合成的結果為 (1)(2,3)=(2,3)。設G表由此6個置換所形成的集合，則合成的運算有如下的性質：

: 一、若g₁，g₂在G內，則其合或g₁g₂也在G內。
: 二、若g₁，g₂，g₃在G內，則 ((g₁g₂)g₃)=(g₁(g₂g₃))。(結合律)
: 三、G中有一元素e[=(1)]，它有如下的性質:eg=ge=g，對所有G中的元素g都對。
: 四、若g在G內，則G中必有一元素g^-1，使得 gg^-1=g^-1g=e。(g^-1稱為g的逆元素。)

一般而言，若G是一個集合(不管有限或無限)，而對應於其中任兩元素g₁，g₂，都有一元素g₁g₂，稱為g₁，g₂兩元素的合成，並且滿足以上四個條件，則稱G為一個群。

群的例子很多，上述所言三個根的置換就成為一個群，稱為三階置換群。又如，整數(或有理數)在加法合成之下成為一個群;非0有理數在乘法合成之下也成為一個群等等。群的合成運算雖然符合結合律，但卻不一定符合交換律。譬如，在三階置換群中，我們已經看過 (1,2)(1,3,2)=(2,3)，然而倒過來合成，則 (1,3,2)(1,2)=(10xA1413)。

現在我們以群的觀點重看三次方程式的解法。我們以S₃表示此三階置換群。讓H表S₃中的元素使y₁³， y₄³不變者(即，讓y₁，y₂，y₃互變;y₄，y₅，y₆互變者)，則

H=(1),(1,2,3),(1,3,2)

在H中仍然有合成運算，而且仍然滿足群的四個條件，所以H也是一個群。但H含於S₃中，而且所用的合成運算相同，所以我們說H是S₃中的一個子群。在S₃中而不在H的元素集合可表成為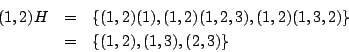

$\begin{eqnarray*} (1,2)H &=& \{ (1,2)(1),(1,2)(1,2,3),(1,2)(1,3,2)\} \\ &=& \{ (1,2),(1,3),(2,3)\} \end{eqnarray*}$

它使y₁³變成y₄³，而使y₄³變成y₁³。簡單地說，H，(1,2)H都可以看成預解式兩根y₁³,y₄³的置換。

再看四次方程式。我們以S₄表示相應的四階置換群。它的元素一共有24個，我們以下表列出:

$\begin{displaymath} \begin{tabular}{\vert c\vert c\vert c\vert c\vert c\vert c\v... ...ries{m}\selectfont \char 98}}&6&8&3&6&1\\ \hline \end{tabular}\end{displaymath}$

所謂類型(1,2,3,4)是指四個數字都出現在同一括弧內者,如(1,2,3,4)等,一共有 $\frac{4!}{4}=6$ 個(環狀排列).其餘類型的意義類推.

在S₄中讓 y₁=x₂x₃+x₁x₄, y₂=x₁x₃+x₂x₄, y₃=x₁x₂+x₃x₄都不變者,仍然組成一個子群.

H={ (1),(1,2)(3,4),(1,3)(2,4),(1,4)(2,3)}

在S₄中而不在H的元素可分成五個子集合(不是子群):

(1,2)H,(1,3)H,(2,3)H,(1,2,3)H,(1,3,2)H

連H[=(1)H]共有6個子集合，而同一子集合中的元素都引起y₁,y₂,y₃ 間同樣的置換。因此這6個S₄的子集合都可看成預解式三根y₁,y₂,y₃ 的置換; $(1)H\rightarrow(1)\in S_3$ , $(1,2)H\rightarrow (1,2)\in S_3$ , $\cdots\cdots$ , $(1,3,2)H\rightarrow (1,3,2)\in S_3$ 。

上述S₃及S₄的H都有如下的性質:gH=Hg對任何g都成立。具有這樣性質的子群稱為正規子群。

如果把三次及四次的想法，拿來看五次方程式，則我們要找根x_i的有理式y_i, $1\leq i$ $\leq m$ $\leq4$ 。然後令H為五階置換群S₅中使y_i都不變的子群，然後把S₅分成為幾個子集合H_i,i=1,…,k的聯集。同一個子集合的元素所相應於y_i的置換都相同，而不同的子集合相應於不同的置換，因此子集合的個數k不能超過m!個;事寶上k要為m!的約數。同時每個子集合的元素個數和H的一樣多，所以H的元素個數正好是S₅的元素個數120的約數。此外， H要為S₅的正規子群。從進一步的群理論，我們知道，除S₅及{ (1)}兩個子群外，S₅只有一個正規子群A₅，其元素個數為60。所以符合上述條件的H只可能是S₅或A₅，而其相應的y_i的個數m就要為1或2。但可證明對一般的五次方程而言，這是不可能的;也就是說，我們找不到適當的y_i，所以用Lagrange的方法無法找到五次方程式的根式解。雖然這並不就證明五次方程式不能有根式解，但卻給這樣的結論提供了強烈的暗示。

受了Lagrange的影響，日後Abel(1802-1829年)終於證明了一般的五次以上方程式沒有根式解，而Galois(1810-1831年)對一個給定的特殊方程式，「何時有根式解，何時則否」，也能根據根的置換原理，而有一定的判斷準則。

由於Lagrange、Abel及Galois等人的努力，根式解方程式的問題終於告了一個段落。然而為了解決這個問題所引起的群理論的探討，本身卻成為現代代數學的一支。經過一個半世紀的演變，群論本身不但有豐富的內涵，而其觀念與應用不只是遍及數學各個角落，而且更侵入了晶體學、化學、物理等領域。

對外搜尋關鍵字：
．Lagrange
．正規子群
．Abel
．Galois
．方程式論


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：鄧惠文

最後修改日期：4/29/2002