Poisson 分布

．原載於科學月刊第十六卷第七期
．作者當時任教於台大數學系

Poisson 分布

曹亮吉

二項分布是離散型機率模型中最有名的一個，其次是 Poisson 分布，它可以看成為二項分布的一種極限情形。

假定某機關的總機在一個短時間 $\triangle t$ 內會接到一次電話的機率 p 與 $\triangle t$ 成正比： $p=\alpha\triangle t$ ，α 為一常數。又假定在此短時間內接到多於一次電話的機率微乎其微，可以略去不計。那麼在時間 t 內，會接到 x 次電話的機率分布為何？

我們可以把 t 分成 n 小段，每小段長為 $\triangle t=\frac{t}{n}$ 。整個問題可看成為：在每個 $\triangle t$ 時間內，我們做了一次試驗，其成功（接到電話）的機率為 p。如此做了 n 次，那麼成功了 x 次的機率為何？所以我們要的機率分布正是二項分布 b(x;n,p)。令 $\lambda = \alpha t = n\alpha\triangle t = np$ ，則

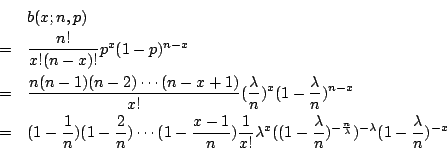
$\begin{eqnarray*} &&b(x;n,p)\\ &=&\frac{n!}{x!(n-x)!}p^x(1-p)^{n-x}\\ &=&\fra... ...}{n})^{-\frac{n}{\lambda}})^{-\lambda}(1-\frac{\lambda}{n})^{-x} \end{eqnarray*}$

當 t 保持不變（亦即 λ 不變），而讓 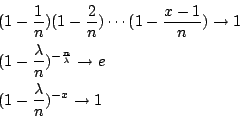$n\rightarrow\infty$ ( $4t \rightarrow 0$ )，則

$\begin{eqnarray*} && (1-\frac{1}{n})(1-\frac{2}{n})\cdots(1-\frac{x-1}{n})\right... ...da}}\rightarrow e \\ && (1-\frac{\lambda}{n})^{-x}\rightarrow 1 \end{eqnarray*}$

所以

$b(x;n,p)\rightarrow\frac{\lambda^xe^{-\lambda}}{x!}$ （以 $p(x;\lambda)$ 表之，此處的 p 代表 Poisson）

因為

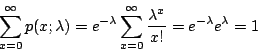
$\begin{displaymath} \sum_{x=0}^{\infty}p(x;\lambda)=e^{-\lambda}\sum_{x=0}^{\infty}\frac{\lambda^x}{x!}=e^{-\lambda}e^{\lambda}=1 \end{displaymath}$

所以 $p(x;\lambda)$ 的確是個機率分布（各種可能的機率之和等於 1）。

這就是說，在時間 t 內，接到 x 次電話的機率為 $p(x;\lambda)$ 。這是以 λ 為參數的 Poisson 分布，而 λ（ $=\alpha t$ ）是在時間 t 內所期望接到的電話數。

Simeon D. Poisson（1781～1840年）是一個著名的法國數學家及物理學家。到了晚年，他熱衷於將數學的機率論用到司法的運作上。他在這方面的主要著作是1837年出版的《司法機率的研究》(Recherches sur la Probabilité des Jugements)。雖然這本書的主旨是要對司法運作有具體的貢獻，但它包含了許多純粹數學的、機率的理論，所以可以看成是一本以司法應用為例的機率課本，這本書德文版的書名《機率論及其重要應用》(Lehrbuch der Wathrscheinlichkeitsrechnung und deren wichtigstein Auwendungen) 看起來和內容較為一致。在這本書的數學推演中，Poisson 從二項分布的極限得到了這個日後以他為名的機率分布。

Poisson 雖然得到這樣的機率分布，但在書中他並沒有繼續討論這種分布的性質，在往後的研究中，Poisson 似乎也把它忘掉了。

在十九世紀的許多統計研究報告上，Poisson 這個名字經常出現，但這與 Poisson 分布無關，大家所關注的是他在常態分布方面的研究。常態分布在解釋理論與數據變異之間的關係非常成功，當時許多人認為常態分布是機率與統計之間唯一的橋梁了。

直到十九世紀末，Bortkiewicz 才注意到 Poisson 分布與某些數據之間也有類似的關聯。Ladislaus von Bortkiewicz（1868～1931年）是出生在俄國聖彼得堡的波蘭人。他在德國 Göttingen 大學得到學位（1893年），並曾在 Strassburg 做過研究。在 Strassburg 時，他寫了一本小冊子《小數法則》(Das Gesetz der Kleinen Zahlen)，專門研究 Poisson 分布。他不但在理論方面推演了 Poisson 分布的許多性質，並且在應用方面，也比較了一些實際發生的、有關於自殺或意外傷害的數據。Poisson 分布雖然出於 Poisson 之手，但真正使它為人重視，使它成為統計學一部分的可要算是 Bortkiewicz了。

在這本書中，Bortkiewicz 舉了一個至今仍是膾炙人口的例子，說明數據契合 Poisson 分布的情形。從1875到1894年的20年間，德國的十四個軍團部有士兵被馬踢傷因而致死的人數紀錄。這 20×l4 = 280個（團年）紀錄，按死亡人數來分，則如表一的左二欄所示。

x=每年死亡人數	團年數	280p(x;0.7)
0	144	139.0
1	91	97.3
2	32	34.1
3	11	8.0
4	2	1.4
$\geq5$	0	0.2

在280個紀錄中，死亡的人數共有196，因此致死率為 $\alpha=96/280=0.7$ （人/團年）。我們就以此 α 為 Poisson 分布中的常數，t=1 年，則 $\lambda=\alpha t=0.7$ 。理想中每團每年死亡人數 x 要遵行 Poisson 分布 p(x;0.7)。表一中右欄就是根據這樣的 Poisson 分布，把280團年該有 x 人死亡的團年數列出。它和表一的中間一欄的數據的確相當吻合。

Poisson 分布既然是二項分布的極限情形，反過來 Poisson 分布也可以做為二項分布的近似值。譬如 p=0.04,n=49，則 $\lambda=49\times 0.04=1.96$ 。我們把 b(x;49,0.04) 與 p(x;1.96) 之值相對照就得表二

x	b(x;49,0.04)	p(x;1.96)
0	0.135	0.141
1	0.276	0.276
2	0.276	0.270
3	0.180	0.176
4	0.086	0.086
5	0.032	0.034
6	0.010	0.011
7	0.003	0.003
8	0.001	0.001
$\vdots$	$\vdots$	$\vdots$

我們發現對應的值相當接近。一般，若用列表方式，則二項分布 b(x;n,p) 要兼顧三個變數 x,n,p，而 Poisson 只要兩個：x,λ，所以較為方便。若直接計算，則因

b(x;49,0.04)=C_x⁴⁹(0.04)^x(0.96)^49-x

所以二項分布算起來相當費事。另一方面 $p(x;\lambda)$ 之值可用遞迴方法迅速求得： $p(x+1;\lambda)/p(x;\lambda) = \lambda/x+1$ 或 $p(x+1;\lambda) = \lambda p(x;\lambda)/x+1$ ；而 $p(0;\lambda)=e^{-1}$ 可由指數表中查得。因此只要情況適合，我們當然就捨二項分布而就 Poisson 分布了。

通常只要 n 很大，p 很小， $\lambda=np$ 不大不小而且是個已知定數，Poisson 分布就可以代替二項分布了，譬如某商店每星期進進出出的客人很多（=n），但每個客人買魚子醬的機率很小（=p），只知道平均一星期賣出兩罐： $\lambda=np=2$ 。那麼這家商店每星期開始時應有幾罐魚子醬的庫存？當然不能只有兩罐，因為平均歸平均，售量超過平均數的機率很大。當然庫存太多也會影響整個商店的運作。根據 Poisson 分布 p(x;2)，我們算得表三：

λ	0	1	2	3	4	5	$\geq6$
p(x;2)	.135	.271	.271	.180	.090	.036	.017

由表三可知售量達到 5 罐以上的機率只有 5.3%，而達到 6 罐以上則只有 1.7%。所以合理的庫存量為 4 罐（平均19星期才會有一次缺貨），如果怕萬一，那麼 5 罐就非常保險（平均59星期才會有一次缺貨）。

我們從另一個角度來看上面的數據。假設某工廠每做100個螺絲釘，平均會有兩個不合規格，而這是合理的不合格率。根據 Poisson 分布，偶而出現 3 個或 4 個不合規格的螺絲釘也是正常的現象。但是如果出現的頻率太高，或出現 5 個以上的不合規格的螺絲釘，那麼生產過程就可能出了問題。Poisson 分布是品質管制的利器，它可以幫助我們決定生產過程是否出了毛病。

Poisson 分布還有種種的用途：放射性物質的蛻變、細胞間因受 X 光照射而引起的染色體交換次數、細菌和血球的計數、交通事故數及死亡率等等莫不遵行 Poisson 分布。其實，無論在自然科學、在工業、在農業、在商業、在醫藥、在交通、在社會或在軍事上，無不可找到 Poisson 分布的應用。

和二項分布一樣，我們也可以從理論方面來探討 Poisson 分布的期望值 μ 及散布差 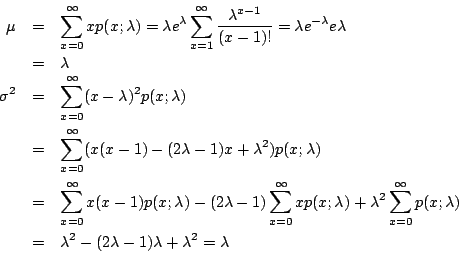$\sigma^2$ 。由 $p(x;\lambda)=\lambda^xe^{-\lambda}/x!$ ，我們馬上算得

$\begin{eqnarray*} \mu &=& \sum_{x=0}^{\infty}xp(x;\lambda) = \lambda e^{\lambda... ...lambda) \\ &=& \lambda^2-(2\lambda-1)\lambda+\lambda^2=\lambda \end{eqnarray*}$

所以 Poisson 分布的確是以 λ 為期望值。

在〈二項分布與大數法則〉（《科學月刊》第十六卷第六期）一文中，我們曾導出二項分布的 Chebyshev 不等式

$\begin{displaymath} (\vert\frac{x}{n}-\mu\vert > \epsilon \; \mbox{{\fontfamily{... ...}\selectfont \char 48} } ) \leq \frac{\sigma^2}{n^2\epsilon^2} \end{displaymath}$

如果把二項分布換成 Poisson 分布或任何離散型分布，不等式也照樣成立，因為在導出不等式的過程中只用到 b(x;n,p) 是種機率分布這件事，並沒有用到 b(x;n,p) 之值。現在既然知道 Poisson 分布的 $\sigma^2$ （=λ）是個（與 n 無關的）定值，所以我們也可以得到關於 Poisson 分布的大數法則：

$\begin{displaymath} \lim_{n\rightarrow\infty}(\vert\frac{x}{n}-\lambda\vert > \e... ....1pt{\fontfamily{cwM7}\fontseries{m}\selectfont \char 48} })=0 \end{displaymath}$

亦即：在 Poisson 分布的機率模型假定之下，只要試驗的次數 n 夠大，則事件發生的次數比 $\frac{x}{n}$ ，從機率的觀點來看，就會很接近期望值 λ。

對外搜尋關鍵字：
．Poisson
．常態分布
．Chebyshev


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：李渭天

最後修改日期：2/17/2002