寫到這兒我們可以開始來介紹董教授畢生功力之所集的一本奇書了,這本書名叫《結構的穩定性與形態學》1。
一九七二年先以法文出書,一九七五年英譯改良本也相繼問世,全書十三章中只有第五章講到基本劇變論,可見把基本劇變論拿來充當董教授的整個劇變論介紹是非常不恰當的。董教授曾經引了一首詩來指明他心中所想處理的問題:
「生活在謎樣的世界裏,
我們可以看到;
海中的波濤起伏,
岸邊的圈圈漣漪
蜿蜒的沙灘
起伏的山丘
天上的浮雲,嬝娜的輕煙……。」
其中充滿了形態學裏,我們所想討論的眾多形相。董教授所想要處理的形相之演
變的問題,其實是人類自古以來所思考的一個中心問題。儘管我們仍對其最終
的本性不甚了然,但是無可否認,我們藉著觀察所見到的宇宙是一個正在運
行,永恒變動的宇宙,各種形相不停地在顯現,演化終又趨於毀滅消失。在錯綜紛
亂的現象之下隱隱含有秩序與條理,但卻又常帶有不確定性的成分,或者
涉及不連續的突然的劇變。董教授所創用的處理這些現象的法寶便是他所謂的局
部模型 (local model),我們這兒只用一個最簡單的例子來講一個最簡單的
局部模型。
首先如果用R表示所有的實數,而用L(R,R)代表所有可微函數f(x)全
體。(圖三)例如一個多項式像P(x)=Pa(x)=
 ,便是可微
函數,它的導數是P'(x)=x2+a。如果以 ,便是可微
函數,它的導數是P'(x)=x2+a。如果以 代表無窮大則 代表無窮大則 =
= ,P(0)=0, ,P(0)=0, = = ,因此函數曲線y=P(x)可能從
正無窮大一直遞降到零,再一直遞降到負無窮大,這時函數曲線根本沒有什麼極大
或極小。但是也有可能y=P(x)有一個極小以及一個極大如圖所示。有一個很
簡單的方法能分辨上述這兩種不同的情形,我們只需解方程
式P'(x)=x2+a=0,可得如下結果: ,因此函數曲線y=P(x)可能從
正無窮大一直遞降到零,再一直遞降到負無窮大,這時函數曲線根本沒有什麼極大
或極小。但是也有可能y=P(x)有一個極小以及一個極大如圖所示。有一個很
簡單的方法能分辨上述這兩種不同的情形,我們只需解方程
式P'(x)=x2+a=0,可得如下結果:
- 當 a>0 時 x2 = -a<0,故 x 沒有實根,換言之,當 a>0,y=P(x) 沒有任何極大或極小。
- 當 a<0,則 x2 = -a>0,故
 為兩個實根, 為兩個實根, 是 Pa(x)的極小, 是 Pa(x)的極小,
 為其極大。 為其極大。
- 當 a=0 時 x=0 為重根,換言之,極大跟極小因 a 趨近於 0 而愈來愈接近,終於互相碰撞而消失。
通常在數學上我們喜歡說 a<0 之 Pa(x) 與 a>0 之 Pa(x) 具有
不同的拓樸型(topological type),因為前者具有極大與極小,但是後
者卻沒有。如果Pa(x)中之a小於零,則只要a'與a足夠接近的話
,a'仍小於零;因此Pa'(x)同樣有個極大與極小,而與Pa(x)具有
同樣的拓樸型。類似的如果Pa(x)中的a大於零,則只要a'與a足夠
接近的話,a'仍大於零,因此Pa'(x)同樣沒有極大極小,而與Pa(x)
具有同樣的拓樸型。這樣的Pa(x)就叫做(在我們所考慮的多項式中)具有結構的穩定性。但是當a=0時,情形卻大大不同,因為無論取a'如何的接近
0,a'可能是正,也同樣可能是負,因此P0(x)附近總有具有不同拓樸型
的函數Pa'(x),我們就說P0(x)的結構不穩定,這樣的函數就叫做
是個分歧函數(bifurcation function)。在可微函數空間L(R,R)中我們有很
精確的方法能定義兩個函數要如何才稱為具有相同的拓撲型,又如何才具有結構的
穩定性,我們就可以把L(R,R)中所有結構不穩定的函數全體H稱為L(R,R)的分歧子
集。
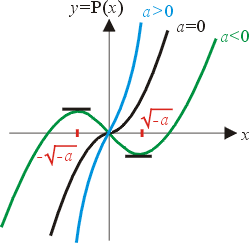
圖三
|
假設某個過程(process)發生在時空中的一個子集W裏,為了描述這個過
程,我們考慮映射g:W L(R,R),對W中之每一點y指定一個
L(R,R)中的函數gy(x),而且要求這樣指定的gy(x)對y在W中的變化而
言需要是可微分的。我們就說g是一個W上的靜態場(static field),它是個
用來描述所考慮之過程的靜態模型(static model)。例如若取W單單代表一條數
軸R,則可以考慮P:R L(R,R),對W中之每一點y指定一個
L(R,R)中的函數gy(x),而且要求這樣指定的gy(x)對y在W中的變化而
言需要是可微分的。我們就說g是一個W上的靜態場(static field),它是個
用來描述所考慮之過程的靜態模型(static model)。例如若取W單單代表一條數
軸R,則可以考慮P:R L(R,R),把任意 L(R,R),把任意 指
定為Pa(x)= 指
定為Pa(x)=
 ,因此P就是R上的一個靜態場。 ,因此P就是R上的一個靜態場。
對於這個特別的靜態場而言,a=0 這點是個特別的點,因為這時 P 所指定的函數 P0(x) 是個分歧函數,它的結構是不穩定的。我們喜歡說這樣的點是我們靜態場中的一個劇變點 (catastrophe point)。原因很簡單,我們如果把 P(x) 想像成是個位函數 (potential function),則位函數的極小常代表某種穩定的平衡而具有物理意義。換言之,如果在某點 a 所指定的 Pa(x) 具有一個極小,那麼我們就解釋說在這一點我們觀察到了某種物理現象,反過來,如果在某點 a 所指定的 Pa(x) 根本就沒有極小,我們就解釋說這時我們根本沒有觀察到任何物理現象。在我們這例子中,如果特別令 a 代表時間,則 a 經 0 點變到負值,就代表某種物理現象在 a=0 時突然的出現,
若 a 經 0 點變到正值,就代表某種物理現象在 a=0 時突然的消失,因此 a=0 這點就是一個發生突然劇烈變動之點,或稱為劇變點。
董教授書中的第一章到第四章裏大量地運用最現代的數學工具與術語考慮靜態模型,還有動態模型 (metabolic model) 以及各種的構造。他又特別運用結構穩定性的考慮來獲得局部模型中所必需特別注意的,W 中所有的劇變點的集合K以及其拓樸結構。如果一個人具有適當微分拓樸 (differential topology) 的知識,那麼這四章並不太難懂。前面已經提及第五章講到四維時空中基本劇變論裏的七種基本劇變模型。從第六章開始董教授漸漸的把劇變論應用到生物學之中。特別從第九章開始變得十分難讀,但卻又十分吸引人。他認為,如同我們可以把物質看成是一個能量場中穩定的奇異點 (singularity),我們也可以把所有生物的個體視為是一個生命形態場 (morphogenetic field) 中穩定的奇異點。他喜歡把這個生命形態場稱為logos,這 logos 翻譯出來就是「道」,就是
「K o o


 」
(道成了肉身)中的「道」,因此他就把這一句約翰福音中的經節拿來做為他的第
九章的子標題。而在第九章中他創造一個看來很不錯的胚胎學中的局部模型,然
後轉而運用在第十章中以創造生物個體的大域模型。最後的三章留下來探討生物
學中一些基本的問題,以及把劇變論更廣泛地運用到語意學及其他課題之中。 」
(道成了肉身)中的「道」,因此他就把這一句約翰福音中的經節拿來做為他的第
九章的子標題。而在第九章中他創造一個看來很不錯的胚胎學中的局部模型,然
後轉而運用在第十章中以創造生物個體的大域模型。最後的三章留下來探討生物
學中一些基本的問題,以及把劇變論更廣泛地運用到語意學及其他課題之中。
說實在的,這是一本很難的書,想要完全讀通幾乎是不可能的事。但是書中卻
也包含不少比較不那麼難懂,而且已足夠讀者吟詠體會不止的部份。這本書中
的一些基本觀點及努力嚐試想完成的目標,其實有些早在數千年前就有古人
這樣想過,只不過那些古人運氣不好,沒有現代的數學像微分拓樸的知識
可用,所以講起來總是些「空話」。但是董教授卻截然不同,他不僅具備現
代數學各領域的知識,而且就微分拓撲而言更是數一數二的高手。例如他所創用的同
境(bordism)的觀念便被陳省身教授稱譽為現代最偉大又重要的數學觀
念之一。於是他充分地運用這些工具而把一些古人的想法講得齊備。因此
他喜歡說他自己的一些工作只是古人思想「遙遠的迴響」(distant echo)。
這是一本很有趣的奇書,這本書曾經引起不少的議論與爭執,卻也引起同
樣許多的讚美與推崇。有些人把它奉為圭皋,但有些人卻認為跟他「道不同不相為
謀」。不過無論如何,漸漸的這書已開始得到更多人的喜愛、瞭解與重視。更多的人同意
這是本超越我們這時代太遠的鉅著,更多的人深信董教授在這書裏所努力創導
的這一套革命性的數學思潮將形成一股愈湧愈盛的泉源,滋潤自然哲學豐腴的
園地。如同相對論經過了這麼多年,終於被大家所樂意接納,也許經過一兩
代之後,董教授的劇變論終將也被普遍接納,又被發揚光大。董教授對於這一點
充滿了信心。
原科月編者按:數學在社會科學上的運用本來也有一些。譬如計算方法、計量方法(如計量經濟學)等;又譬如統計、或然率、圖形、微積分(如處理極大、極小)等,在處理定性方面的問題都有相當的成就。只是對不連續現象(不論發生在社會科學、生物科學或自然科學)的研究卻一直沒有很有力的工具。劇變論或許能彌補這方面的缺憾吧!
- 1. René Thom, 《Structural Stability and Morphogenesis》, 1975. Benjamin Inc.
- 2. R. Thom, 〈La Theorie des Catastrophes: Etat present et Perspectives〉, Dynamical Systems-Warwick 1974. Springer Notes # 468.
- 3. E.C. Zeeman, 〈Catastrophe Theory: A reply to Thom〉, Same as (2).
- 4. E.C. Zeeman, C.A. Isnard, 〈Some Models from Catastrophe Theory in the Social Sciences〉, Warwick Notes.
- 5. J. Croll, 〈Is Catastrophe Theory Dangerous?〉 New Scientist, 17. June, 1976.
- 6. 蕭欣忠,《劇變論演講集》,淡江數研所,1976.
|