凸函數、Jensen 不等式與 Legendre 變換 (第 5 頁)

　1│2│3│4│5　

凸函數、Jensen 不等式與 Legendre 變換（第 5 頁）

林琦焜

首頁 | 搜尋

．原載於數學傳播第十九卷第四期
．作者當時任教於成大數學系
‧對外搜尋關鍵字

五、Jensen 不等式之應用

應用一

任給兩個正數 a,b，其 p 階平均為

$\begin{displaymath} N_p\equiv[\theta a^p+(1-\theta)b^p]^{\frac{1}{p}} \eqno{(37)} \end{displaymath}$

現在考慮函數 $f(x)=x^{\frac{q}{p}}$ ,p<q，因為 $\frac{q}{p}>1$ ，故 f 為一凸函數 (convex function)。因此由 Jensen 不等式知

$\begin{displaymath} f(\theta a^p+(1-\theta)b^p)\leq\theta f(a^p)+(1-\theta)f(b^p) \end{displaymath}$

即

$\begin{eqnarray*}[\theta a^p+(1-\theta)b^p]^{\frac{q}{p}} & \leq & \theta a^{p ... ...heta)b^{p \cdot \frac{q}{p}} \\ & = & \theta a^q+(1-\theta)b^q \end{eqnarray*}$

故

$\begin{displaymath} \begin{eqalign} N_p & = [\theta a^p+(1-\theta)b^p]^{\frac{1}... ...a^q+(1-\theta)b^q]^{\frac{1}{q}}=N_q \end{eqalign} \eqno{(38)} \end{displaymath}$

即如果將 N_p 視為 p 之函數，則 N_p 為 p 之增函數。同理可得積分形式的 p 階平均：

$\begin{displaymath} N_p[f] \equiv \Big( \frac{1}{\vert\Omega\vert}\int_{\Omega}\... ...f\vert^p \Big)^{\frac{1}{p}}, \quad 0<\vert\Omega\vert<\infty \end{displaymath}$

則

$\begin{displaymath} N_{p1}[f]\leq N_{p2}[f], \quad P_1<p_2 \eqno{(39)} \end{displaymath}$

其中 $\vert\Omega\vert$ 表示 Ω 之面積或體積。讀者若有實變函數論的觀念，則(39)式所表示的函數空間之關係為

$\begin{displaymath} L^{p2}(\Omega)\subseteq L^{p1}(\Omega), \; \frac{1}{p_2}\leq\frac{1}{p_1}, \; \vert\Omega\vert<\infty \eqno{(40)} \end{displaymath}$

其中函數空間 $L^P (\Omega)$ 表示 p 次方後可積分之函數所形成之集合

$\begin{displaymath} L^P (\Omega)= \Big\{ f \big\vert \int_{\Omega}\vert f\vert^P dx < \infty \Big\} \eqno{(41)} \end{displaymath}$

要特別叮嚀的是(40)式之關係，只有在 $\vert\Omega\vert<\infty$ 之條件下才成立，因為此時質量中心才有定義。

應用二

凸函數在二維或更高維數的空間，例如複變函數，所對應的便是次調合函數 (subharmonic function)

$\begin{displaymath} \triangle u\geq 0 \eqno{(42)} \end{displaymath}$

對於此類函數具有非常重要地位的平均值不等式 (mean-value inequality) 為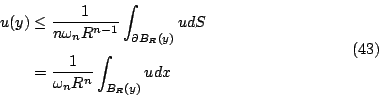

$\begin{displaymath} \begin{eqalign} u(y) & \leq \frac{1}{n \omega_n R^{n-1}}\int... ...c{1}{\omega_n R^n}\int_{B_R (y)}u dx \end{eqalign} \eqno{(43)} \end{displaymath}$

B_R (y) 表示以 y 為圓心，半徑為 R 之 n 維球， $\partial B_R(y)$ 則表示其球面， $\omega_n$ 為 n 維單位球之體積。(43)式實際上就是 Jensen 不等式之一特例，但要特別叮嚀的是(41)式之積分區域務必要取均勻的球 B_R (y) 或球面 $\partial B_R(y)$ ，因為此時 y 是 B_R (y) 或 $\partial B_R(y)$ 的質量中心。由(43)式可推得最大值原理 (maximum principle)。

定理最大值原理（maximum principle）：
$u \in C^2 (\Omega) \cap C^0 (\overline{\Omega})$ , $\Delta u \geq 0$ ，則

$\begin{displaymath} \max_{\overline{\Omega}}u=\max_{\partial\Omega}u \eqno{(44)} \end{displaymath}$

這定理告訴我們一個定義在有界區域 Ω 之次調合函數，其最大值必定發生在邊界 $\partial\Omega$ 上。關於這件事實，我們亦可以凸函數之性質來想像。讀者可參考底下之圖形

圖九

另外在偏微分方程中的 Laplace 方程 $\Delta u=0$ ，解之存在性證明方法中的 Perron 方法，也可由此角度來思考。

圖十

D. Gilbarg and N.S. Trudinger, Elliptic Partial Differential Equations of Second Order, 2nd ed., Springer-Verlag (1983).
G.H. Hardy, J.E. Littlewood and G. Pólya, Inequalities, Cambridge University Press, Cambridge (1952).
Fritz John, Partial Differential Equations, 4th ed., Appl. Math. Sci., 1, Springer-Verlag (1982).
T. Needham, A Visual Explanation of Jensen's Inequality, American Math. Monthly 100, 768-771 (1993).

　1│2│3│4│5　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：黃信元 ∕ 繪圖：張琇惠、簡立欣

最後修改日期：4/26/2002