| |
Cayley 數是由四元數 H 加入另一單位 e 而得,即
乘法的定義是
Cayley 數 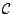 中,除 H 中原來就有的 4 個單位 1,i,j,k 外,另由 e 與這四個單位相乘而得出四個單位。因此 C 中共有 8 個單位;
而以 e0(=1),e1,e2,e3,e4,e5,e6,e7 分別表示,這些單位與原先單位 i,j,k,e 的關係為 中,除 H 中原來就有的 4 個單位 1,i,j,k 外,另由 e 與這四個單位相乘而得出四個單位。因此 C 中共有 8 個單位;
而以 e0(=1),e1,e2,e3,e4,e5,e6,e7 分別表示,這些單位與原先單位 i,j,k,e 的關係為
e0=1,e1=j,e2=i,e3=e,e4=-k,e5=ie,e6=ke,e7=je
每一Cayley數都可表成
而單位之間的乘法滿足下面的法則:
-
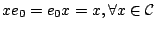
-
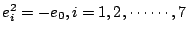
-
e1e2e4=e2e3e5=e3e4e6=e4e5e7=e5e6e1=e6e7e2=e7e1e3=-e0
現將上面的法則說明如下:
第一式表明e0=1是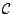 中乘法 中乘法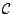 的單位元素。 的單位元素。
第二式表明8個單位,除e0外,其他的7個單位的平方都是-1,故方程式x2+1=0在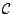 中至少會有7個解。 中至少會有7個解。
第三式中,列出一些可結合之單位的連乘積。直接的驗證顯示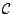 中的乘法沒有結合律,即 中的乘法沒有結合律,即
(xy)z=x(yz)
不一定成立;而在沒有結合律的乘法中,(3)式中的連乘積應是沒有意義。但事實並沒有想像中的壞,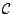 中的某些單位的乘積確有結合律。以
e1e2e4=-e0來說,這式子表示的意義有二:
中的某些單位的乘積確有結合律。以
e1e2e4=-e0來說,這式子表示的意義有二:
-
e1(e2e4)=(e1e2)e4=-e0
-
e1e2=-e2e1=e4,e2e4=-e4e2=e2,e4e1=-e1e4=e2
回顧一下,四元數H中的單位i,j,k也具有同樣性質,
因而H與
R e0+R e1+R e2+R e4也同樣的代數結構。
當然
e1,e2,e4只是(3)式的一特例,另外尚有6個,
如
e2e3e5=-e0也表示
R e0+R e2+R e3+R e5與H有相同的代數結構。
現在來看兩個不可結合的例子。
(e1e2)e3=e4e3=-e3e4=-e6
另一方面
e1(e2e3)=e1e5=e6
故
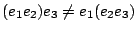 又 又
上面例子顯示單位相乘,因不具結合性,算出的結果會有符號上的差異。
Cayley數中,
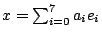 的共軛數定為 的共軛數定為
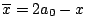 ,亦即 ,亦即
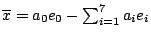 。又範數N的定義是 。又範數N的定義是
因而,若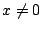 ,則x有一乘法反元素[N(x)]-1x。 ,則x有一乘法反元素[N(x)]-1x。
證明
N(XY)=N(X)N(Y)並不簡單,這要用到一些特殊乘積的結合性,即
將
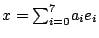 與 與
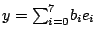 代入
N(XY)=N(X)N(Y)中即得出下
面的等式: 代入
N(XY)=N(X)N(Y)中即得出下
面的等式:
其中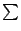 表示將足碼0固定,而將1,2,3,4,5,6,7依循環次序變換,如依次變換為2,3,4,5,6,7,1。
注意等式右邊的八個數也正好是 表示將足碼0固定,而將1,2,3,4,5,6,7依循環次序變換,如依次變換為2,3,4,5,6,7,1。
注意等式右邊的八個數也正好是
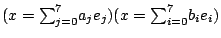 之乘積的8個係數。
之乘積的8個係數。
實數R、複數C,四元數H與Cayley數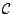 都可以看成佈於R的向量空間,維數分別是1,2,4,8。
在高中階段,對C已非常熟習;但對H與 都可以看成佈於R的向量空間,維數分別是1,2,4,8。
在高中階段,對C已非常熟習;但對H與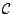 知道的人,可能非常少,甚至有些人並不知道。 知道的人,可能非常少,甚至有些人並不知道。
|
|
|