| |
|
5.大離差(Large Deviations)與正規逼近(Normal Approximation): |
弱大數法則告訴我們
 趨近於0。
在實際應用中我們常常希望知道這個量趨近於0的速度有多快。這方面的研究屬於大離差理論的範疇。
它的一個基本結果是Cramer所證 趨近於0。
在實際應用中我們常常希望知道這個量趨近於0的速度有多快。這方面的研究屬於大離差理論的範疇。
它的一個基本結果是Cramer所證
-
- 定理:
假設
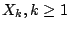 是i.i.d.,且Xi的moment generating function 是i.i.d.,且Xi的moment generating function
對任意實數 t 都成立。定義
則對任意R上的一閉集F,
對R上的任一開集G
定理的I稱做速率函數(rate function),
 ,在 ,在 的部份它是一個凸函數,
的部份它是一個凸函數, ,且I(x)在 ,且I(x)在 是漸增,在 是漸增,在![$(-\infty,\mu]$](img158.gif) 是漸減。
因此在許多情況下若 是漸減。
因此在許多情況下若 則I(x)>0。譬如說在例2.2的Bernoulli trial 則I(x)>0。譬如說在例2.2的Bernoulli trial 此時 此時
於是若令
![$F=(-\infty,p-\varepsilon]\cup[p+\varepsilon,\infty]$](img162.gif) ,則由(5.1)式 ,則由(5.1)式
另一方面令
 ,則由(5.2)式 ,則由(5.2)式
故而綜合可得
令右式為a,則a<0,且上式表示
換句話說
 是以指數的速度漸趨於 0。 是以指數的速度漸趨於 0。
上述所提是大離差理論的一些較古典的結果,最近十九年已有很多深入的發展。
目前機率界有一些人從事這方面的研究。
[5]是大離差理論的一本「比較」容易看懂的書。有興趣的讀者可以參考它。
與上面類似的一個問題是探討中央極限定理(見(3.1)式)裡 Fn(x) 收斂到 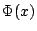 的速度。除了中央極限定理的要求,若進一步要求 的速度。除了中央極限定理的要求,若進一步要求
 ,則 Berry-Essen 證明了存在一常數 A0 使得 ,則 Berry-Essen 證明了存在一常數 A0 使得
在更強的假設下,Cramer及Hsu(許寶騄)得到下面的展式
其中Hn(x)是與Hermite多項式有關的函數。這些結果屬於Normal Approximation的範圍。
- 1. Y.S.Chow(周元燊)and H.Teicher,《Probability Theory》, Springer-Verlag, New York, 1978.
- 2. K.L Chung(鍾開萊),《A Course in Probability Theory》, Academic Press, New York, 1974.
- 3. W.Feller, 《An Introduction to Probability Theory and its Applications》, vol 1, 2nd ed., Wiley, New York, 1968.
- 4. W.Feller, 《An Introduction to Probability Theory and its Applications》, vol 2, Inded., Wiley, New York, 1971.
- 5. D.W.Stroock, 《An Introduction to the Theory of Large Deviations》, Springer-Verlag, New York, 1984.
|
|
|