偽畫鑑定

．原載於數學傳播第七卷第三期
．作者當時任教於交大應數系

‧註釋

偽畫鑑定
微分方程的應用

林朝枝

二次世界大戰後期，盟軍收復比利時之後，荷蘭治安人員開始通緝納粹同路人。在一家曾經出售許多藝術品給德國人的公司記錄上，他們發現一位銀行家的名字，他曾是將著名的十七世紀荷蘭畫家 JAN Vermeer 的油畫： "Woman Taken in Adultery" 出售給納粹頭目戈林的中間人。由銀行家口中得知他是代表一個三流荷蘭畫家 H.A. VAN Meegeren。 1945年5月29日 VAN Meegeren 被控通敵罪名而被捕入獄。 1945年7月12日 VAN Meegeren 在獄中傳出一個震驚世人的話，聲稱他不曾對 "Woman Taken in Alultery" 賣給戈林。同時，他說這幅畫和另一幅美麗的畫："Disciples at Emmaus"，還有其他兩幅被認為是 Vermeers 的作品以及兩幅 de Hooghs（十七世紀荷蘭畫家）的畫都是他自己所偽造的。然而許多人卻認為 VAN Meegeren 說出這類謊言，目的只在於免除他的叛國罪名。為了證實他的話，VAN Meegeren 在獄中開始偽造 Vermeer 的畫："Jesus Amongst the Doctors"，顯示給那些不相信他的人，他確是 Vermeer 畫的偽造高手。當這幅畫接近完成的時候，VAN Meegeren 得知他通敵的罪名已改為偽造罪名，於是他拒絕完成這幅畫和將畫變成古老的樣子，希望調查行動不致發現其將畫變古的秘密。為了解決這個問題，有著名化學家、物理學家和藝術史家受命組成國際專案小組，來調查這個秘密。小組用X-光透視畫件以決定這些偽畫是否畫在其他的畫之上。另一方面，他們分析畫上所用的顏料和畫的某些舊年代的跡象。

然而 VAN Meegeren 對於這些鑑定方法知悉頗詳，為了避免被發現，他將不值錢的古畫的顏料括去，僅只保留畫布，而嘗試使用 Vermeer 可能會用的顏料。 VAN Meegeren 也熟知舊的油彩非常地硬，同時也無法溶解它。因此，他很狡猾地將一種化學物：'Pheno formaldehyde 混入油彩裏，然後當完成的油畫在烤箱中加熱時，油畫就會硬化，因而他人不易知道那是偽畫了。

然而 VAN Meegeren 在他的幾幅偽畫中有所疏忽。專家所組成的鑑定小組發現了一種現代顏料鈷藍的蹤跡。另外，他們在數幅畫中也發現了 Phenoformaldehyde，這種化學物直到十九世紀初才被發現。基於這些證據，VAN Meegeren 於1947年10月12日被判了偽造名畫的罪，入獄一年。在獄期間，他的心臟病發作，於1947年12月30日去世。

但是，即使在專家們搜集了證據，仍有許多人拒絕相信名畫："Disciples at Emmaus 是 VAN Meegeren 所偽造的，他們的想法是基於其他的膺品和 VAN Meegeren 近乎完成的"Jesus Amongst the Doctors" 都是相當低俗的品質。他們認為美麗的 "Disciples at Emmaus" 的創作者絕對不會畫出如此拙劣的畫的。事實上，"Disciples at Emmaus" 曾被著名藝術史家 A.Bredius 鑑定為 Vermeer 的真蹟，而被 Rembrandt Society 以 $170,000 的高價購得。鑑定小組對這些持懷疑態度的人的答覆是 VAN Meegeren 對於他在藝術界毫無地位深感失望，他在畫 "Disciples at Emmaus" 時，欲以無比的決心來證明自己實在不是三流的畫家。在完成這幅傑作之後，他的意志力就消失了，同時，在體認了他能輕易地完成了 "Disciples at Emmaus"，他不再那麼認真地從事其他的偽畫了。這種說法卻不令持懷疑論者滿意，他們要求能提出一種全然科學化和結論性的證據，以證實 "Disciples at Emmaus" 確實是一幅偽畫。1967年美國 Carnegie Mellon 大學的科學家們進行了這項研究，以下就是他們工作的概略描述。

利用放射性的現象來鑑定畫和其他物質──諸如石頭和化石的年代等──的方法是本世紀初所發現的。物理學家 Rutherford 和他的同事們證實了某些放射性的元素之原子結構不穩定，在一個既定的時期之內，固定比例的原子會發生蛻變而形成另一種新元素，由於放射性是原子的一種性質，Rutherford 證實一種物質的蛻變率 ^註1 與該物質目前的原子個數直接成比例。因此，設若 N(t) 表示某物質在 t 時間的原子數，則單位時間內發生蛻變的原子數 dN(t)/dt 與 N(t) 成正比。即:

$\begin{displaymath}\frac{dN(t)}{dt}=-\lambda N(t) \eqno(D)\end{displaymath}$

其中 λ 為一個常數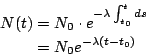， $\lambda >0$ 是為所謂的蛻變常數。當然 λ 越大，物質蛻變得越快。半衰期就是用來計量一種物質發生蛻變情況的單位，我們定義半衰期為放射性原子數目蛻變成原來數目之一半所需要的時間。假設在開始時間,t₀,原子數目為 N₀，即N(t₀)=N₀，則 N(t) 滿足微分方程式：

$\begin{displaymath} \frac{dN(t)}{dt}=-\lambda N(t) \; , \;\; N(t_0)=N_0\eqno(1) \end{displaymath}$

(1)的解是

$\begin{eqnarray*} N(t)&=& N_0\cdot e^{-\lambda \int_{t_0}^{t}ds} \\ &=& N_0e^{-\lambda(t-t_0)} \end{eqnarray*}$

可推得

$\begin{displaymath} \frac{N(t)}{N_0}=e^{-\lambda(t-t_0)} \end{displaymath}$

兩邊取對數函數，則

$\begin{displaymath} -\lambda(t-t_0)=\ln \frac{N(t)}{N_0}\eqno(2) \end{displaymath}$

當

$\begin{displaymath} \frac{N(t)}{N_0}=\frac{1}{2} \end{displaymath}$

則

$\begin{displaymath} -\lambda(t-t_0)=\ln \frac{1}{2} \end{displaymath}$

因此

$\begin{displaymath} t-t_0=\frac{\ln 2}{\lambda} \approx \frac{0.6931}{\lambda}\eqno(3) \end{displaymath}$

也就是說物質的半衰期為 $\ln2$ 被其蛻變常數 λ 來除的結果。很多放射性物質的半衰期都已經被完整地計算，並且記錄下來。像 C-14 的半衰期是5568年，U-238 則為四億五千萬年。

由(2)式可得

$\begin{displaymath} t-t_0=-(\frac{1}{\lambda})\cdot\ln(\frac{N(t)}{N_0}) \end{displaymath}$

因 N(t) 可以測量出來，λ 為已知數或是很容易計算出來，故當N₀知道時，我們就能得到 t₀ 來。事實上 N₀ 的決定就是難處。因為我們不能知曉某種放射性物質在 t₀ 時的原子數有多少?不過，我們還是可以間接地決定N₀之值， (或者估計 N₀ 之值。)使它在某個可信賴的範圍內。估計 N₀ 之值即為我們用來鑑定膺品的方法。我們將在底下概略的解釋這種方法。

地球的地殼中含有鈾的成分，在岩石塊內的鈾會蛻變成其他的放射性元素，然後再經過一連串的蛻變，一直到Pb-206為止，到此它已不含任何的放射性元素了。下表說明U-238的一系列蛻變情形。箭頭上方的數字即為半衰期。

因為鈾-238的半衰期很長，它不會很快消失，當然也會一直的蛻變下去。因此表裏的中間放射性元素，一方面會蛻變成其後面的元素而減少，但一方面也會因前面元素的蛻變下來而增加。

所有畫家所使用的顏料都含有多量放射性元素的鉛-210，同時也含有更少量的鐳-226。因為上述兩種元素含在鉛白內，而鉛白被畫家用做顏料已經有兩千多年的歷史了。鉛白由金屬鉛所製成，而金屬鉛則由鉛礦用熔煉方法提煉出來，在這種提煉過程中，鉛-210會隨著留在提煉後的金屬鉛內，然而百分之九十到九十五的鐳-226會在提煉過程中留在熔渣內而被排除掉。在剛做成鉛白時，因為鐳-226之半衰期為一千六百年，所以蛻變成鉛-210的放射性元素算是很少。但是，由於鉛-210的半衰期為二十二年，因此鉛-210就會蛻變的比較快，而減少了很多鉛-210的原子個數。這種現象會一直下去，直到平衡點。也就是由鐳-226蛻變成鉛-210的原子數目，相等於由鉛-210蛻變成另一種元素的原子數目。又因為從鐳-226蛻變成鉛-210之間那些放射性元素的半衰期與一千六百年互相比較之下，實在太小。若忽略了它們，則我們也可以說鉛-210與鐳-226的蛻變相等時就是所謂的平衡點。

我們用上述的結論，來估計出在最初製造金屬鉛時，鉛-210的含量有多少？令 y(t) 表示在 t 時間每公克的鉛白所含鉛-210的原子數目，y₀ 則是在製造鉛白時 (t₀)，每公克鉛白所含鉛-210的原子數目。也令 r(t) 為 t 時，鉛白中的鐳-226每分鐘每公克蛻變的原子數目。 λ 為鉛-210的蛻變常數，則我們可以得到下列的微分方程式:

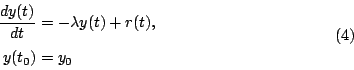
$\begin{displaymath} \begin{eqalign} \frac{dy(t)}{dt} &= -\lambda y(t)+r(t), \\ y(t_0) &= y_0 \end{eqalign} \eqno(4) \end{displaymath}$

這個方程式在 r(t) 不是常數時，求出來的解比較不易說明其結論。我們可以做如下的簡化：因為我們的目的在鑑定一張畫的真偽程度，而這些畫的歷史大都在三百年的時間內。同時鐳-226的半衰期則有一千六百年，含在鉛白內的鐳-226又非常少。所以為了方便，我們不妨假定 r(t) 為一個常數 r。我們來解微分方程式(4)。兩邊乘上其積分因子 $\mu(t)=e^{\lambda t}$ ，我們得到：

$\begin{displaymath}\frac{d}{dt}[e^{\lambda t}y(t)]=re^{\lambda t}\end{displaymath}$

所以

$\begin{displaymath} e^{\lambda t}y(t)-e^{\lambda t_0}y_0 =\frac{r}{\lambda}(e^{\lambda t} - e^{\lambda t_0}) \end{displaymath}$

或者

$\begin{displaymath} y(t)=\frac{r}{\lambda}[1-e^{-\lambda(t-t_0)}] +y_0e^{-\lambda(t-t_0)} \eqno(5) \end{displaymath}$

y(t) 與 r 很容易可以測定出來。故若 y₀ 知道，由(5)式， (t-t₀) 就可以求得，畫的年代由此就知曉了。惟前面已經敘述過 y₀ 不能直接求得。克服這個困難的方法之一是:由於地球的年代已經非常久遠，所以我們可以想像在鉛礦中，鉛-210與鐳-226的蛻變情況已達平衡狀態，即它倆的蛻變速率一樣。當我們抽取地球上的不同礦石來測定鐳-226的蛻變情形。發現鐳-226在不同礦石中每公克每分鐘的蛻變速率是在0.18到140之間。所以推得鉛-210在鉛白內每公克每分鐘的蛻變情形也大致是在這範圍之間。由於這個範圍太大，因此歸納出來的 y₀ 數目也可能會在一段很大的範圍內（因為鉛-210的蛻變速率與其原子數目成正比。）；即鉛-210的原子數目 y₀ 會有很大的變化。所以不能用這種方法來估計 y₀ 之值。但是，我們還是可用(5)式來鑑別出十七世紀的畫與近代的仿製品。若一張畫的年代遠比二十二年（鉛-210的半衰期）還久的話，那麼，鐳-226與鉛-210就幾乎已達平衡點了。反過來說，若是一幅近幾年內的仿製品，比方說是20年的膺品，那麼鉛-210的放射性就要比鐳-226的放射性強得多。讓我們假設某幅欲被鑑定的畫，其年代是否在300年？令 t-t₀=300，由(5)式，我們得到：

$\begin{displaymath} \lambda y_0=\lambda y(t)e^{300\lambda}-r(e^{300\lambda}-1) \eqno(6) \end{displaymath}$

若這幅畫是近幾年來的仿製品，則 $\lambda y_0$ 的值會是一個很大的數，大到令人一看就知道為不可能的情形。但我們又怎樣知道那一個數才是合理？那一個大的數令人覺得不合理呢？首先，我們假設鉛-210在剛製造出來的時候，在鉛白內每公克每分鐘的蛻變速率為100，則推算出採出來的礦石中含鈾-238的比率約為 $0.014 \%$ 。這個含量已算是相當高了，因為地球上的所有礦石含鈾-238的平均數遠低於此數。不過，在西半球有一些稀有的礦石中，則含有 $2 \sim 3\%$ 的鈾-238。所以為了安全起見，我們就說，當鉛-210的蛻變速率超過30000時（此時，在地球上此礦石含鈾-238之比率約為5.2 %），就是個不合理的數目。

因為在幾年後，鉛-210與鉑-210的蛻變情形很快會達到平衡狀態，而且以目前已有的計量方式來說，對鉑-210的測定比較容易。所以我們就用鉑-210來代替鉛-210。又鉛-210的半衰期為22年。故 $\lambda=\ln2/22$ ，所以 $e^{300\lambda}=e^{\frac{300} {22}\ln2}=2^{\frac{150}{11}}$

下面的表是鉑-210與鐳-226在幾幅畫上的蛻變情形：

畫的名字鉑-210蛻變率(每克每分鐘) 鐳-226蛻變率(每克每分鐘)

Disciples at Emmaus 8.5 0.8

Washing of Feet 12.6 0.26

Women Reading Music 10.3 0.3

Women playing Mandolin 8.2 0.17

Lace Maker 1.5 1.4

Laughing girl 5.2 6.0

若把 "Disciples at Emmaus" 這張畫的8.5代入(6)式中的 $\lambda y(t)$ ，把0.8代入(6)式中的 r， $\lambda=2^{\frac{150}{11}}$ ，則我們得到：

$\begin{eqnarray*} \lambda y_0 &=& (8.5)\times2^{\frac{150}{11}}-0.8\times(2^{\frac{150}{11}}-1)\\ &=& 9.8050261204056\times10^{4} \end{eqnarray*}$

所得到的數目大於 3 x 10⁴ 太多，故可以斷定它為一幅假畫。其他幾幅畫的 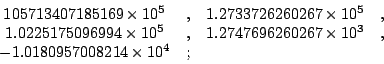$\lambda y(0)$ 的值，經過計算之後，分別為:

$\begin{displaymath}\begin{array}{cccc} 105713407185169\times10^{5}&,&1.273372626... ...7\times10^{3}&,\\ -1.0180957008214\times10^{4}&;&& \end{array}\end{displaymath}$

由此可見前面的三幅畫也該是膺品。至於後面的兩張畫是真品的可靠性就相當高了。

M. Braun: Differential equations with applications.

對外搜尋關鍵字：
．微分方程


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：石莉君 ∕ 校對：楊佳芳 ∕ 繪圖：簡立欣

最後修改日期：4/26/2002