�D�����ƾǶǼ��ĤG���ĤT��
�D�@�̷��ɥ��Щ��j���ƨt
�E����
�i����
|
�D�����ƾǶǼ��ĤG���ĤT�� �D�@�̷��ɥ��Щ��j���ƨt �E���� | |||
|
���ܤשԪ�����
�i���� |
|
���ڰ������ɭԡA���ȩҿסu�s�ƾǡv�}�l���ڡC�u�s�ƾǡv�������A����Ĭ�X�Ĥ@���H�y�ìP�ɪšA��ڤW�����_�夣�w�A����H�����X�ݹέu�X�A��s�X���H��H�@�K����a�Ӧb�ӪŬ�s�譱����C�L�̱o�쪺���ܦh�A�䤤���@�I���X�A����b��Ǥ譱����¦�Ш|����A�Ч����¤��Ź�ڡA��O�U�B�i�}�ҵ{����A��s�åX���s���Ч��C�ڰ���������v�T�A�ﭲ�E�_�C�ڤW�������ɭԡA�u�s�ƾǡv�~�}�l���[�A�ұĨ����Ч��j�P�W���� SMSG (School Mathematics Study Group)�A��S��O�i�o�@���Ϋe�@���~�o�i�X�Ӫ��s�z�סA�p���X�B��B��@�N�Ƶ��F�̭��n���@�I�O�A���A�������c�ƪ��p��H�θ����D���U�O�ޥ��A�N���H�z�ת��@�e�ʤ��Y��ʬ��۲��I�C �n�D�ƾǤW���Y�K�ۦ���`�������v�I���C�ƾǤW��B�R���������ϤH�̤��o���Ĩ��Y�Ԫ��A�סC���O�A�L�S���ΡA�L���j���Y�K�@���A�����Ϫ�Ǫ̤����|�A�Ʀܱ�ӥͬȡC���D�ڭ̹��ҭn�Q�ת��ƪ������w�g�R���A�ѡA�_�h�Y�K���z�S�����n�A�o�˰������������ڭ̪��D��h�A�ϦӬO�@�j��ê�C�ƹ�W�A�ƾǥ������\�h�O�����z�@�ˡA�ݭn�a�g��A�z�L�\�h�S�ҡA�@�A�ϬM�X�䥻��H��A��H�~�O�@��²�䪺�u��A�_�h���{�M�L�ΡC
���ɭԡA�ڭ̷|�o�{�ƾǤW���@���ҩ��ƽ�W�Q���L�ΡC�|�Ҩӻ��A�ҥ��W�s�ڭ��ҩ�
�o�˪����l�X�G�O���ҩP���A�ӥB�O�`�ѯ몺�ݭn�O���C ���ٰO�o�Q���M���A�����ɪ��Ѯv��F�n���@�q�ɶ��A�ܽ�O�������ƾ��k�Ǫk�A�ӥB�@�A�j�աA���F�μƾ��k�Ǫk�A���藍��u�Y��v���ҩ��o�Ӧ��l���ߡC����ܤ[�H��A�ڭ̤j�h�ƤH�٬O����Q���A�Ѽƾ��k�Ǫk������C�ڭ̥u�O�ߺD������ n=1 �N�J�A���ҨS���A�A�q n ���ߡA�ҩ� n+1 ���ߡA�o�L�D�O�b���l��ݦU�[ (n+l)2�A�A��k��ꦨ�J�w�榡�A��O�ھڼƾ��k�Ǫk�A�o�ҡC�ڭӤH���g��F�ܪ��@�q�ɶ��h��ҳo�Ӱ��D�A�ۤv�ݦۤw�A�p�G�D�جO
�o�حn�|���@�ӨҤl�A�O�ש� (Euler) �p��
�f�V�Q (Bernoulli) �O�שԪ������A�L��L�a�żƷ����^�m�A�ר�@�͡A�\�h�żƳ��Q�L��s�L�AĴ�p�A�ۦW���f�V�Q�żƴN�O�]�L�ӦW�C���
�����A�שԪ`�N��h�����کM�Y�ƪ����Y�A�p�G�h����
���ڬO r1, r2,�K,rn�A�h 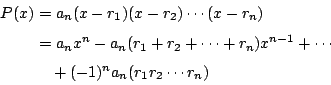
����Y�ƥi�H�o�� ���ڦ����H 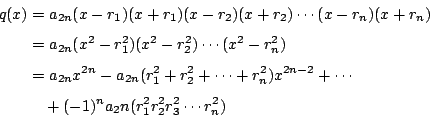
����Y�ơA�h �p�G q(x) �S���s�ڡA�h�Ҽ{ 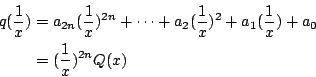
�䤤 ��ګꬰ q(x) �Ѯڪ��˼ơA�Y �W���k�䪺���l�M�ҭn�D�� �שԧ� ��ڬ� ��Y �ڲq�Q�A�p�G�b�Ҹը��W�o�˰������ܡA�j�b���i��O�o��s���C�שԥ��H��o�˪��Ѫk��M�]�ä����N�A�L���չL�U�ب�L�i��A�Q��o�@�Ӹ��������ҩ��F���M�u���p���p���I�H��X��A���H���X���۫H�䥿�T�ʡA���O�Ҧ��H�A�]�A�שԦb���A����믫�h���n���ҩ��C�שԥ��H��Q����������k�A�o��\�h��L�����l�C
�ڷQ�����@�I�O�A���F���סA�A��ۥh�ҩ��䥿�T�ʡA�N��o���ӧ�e���A���Y���F�C�b�o�اڷQ���Ѥ@�Ӱ���k�A�Ȼ����o�@�ǤT�����p��N���A�ӥB�A�������H��A��i�H�D�o�@��
�M�שԪ��Ѫk�ۤϡA�ڭ̷Q��
�� De Moivre �w�z�i�o
�p�G��w�S�O������ �t�@�譱�Q�ΤG�����w�z�i�}�i�o 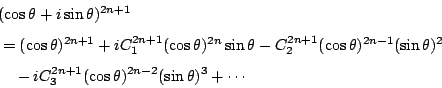
����⦡����Ƴ����A�i�H�o�� 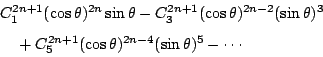
���� 0�C�b�W�����S�O��w���A ���y�ܻ��A�h���� �� 2n �ӫD�s�ڬ� 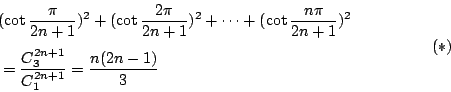
�q�t�@���צ��p�U���M��T����ƭȶ����~�t�A�i�H�o�� �o�@�I�i�ѤU�ϳ��ꤺ���έ��n�ݥX�ӡG
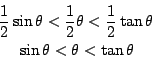
�����A�A�˼ơA�o �N�W���� 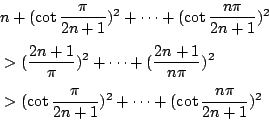
�å�(*)�o ��Y �� �ҥH �]��
[���]�m�ƾǶǼ��n�u�Z�ĥ|�����۩w���͡q�Ʈe��z�r�@��A��86���A���@�����D�ءG
�u�] n �O�۵M�ơA�G��ƺ��� 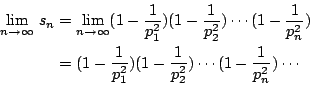
�q�t�@�Ө��� 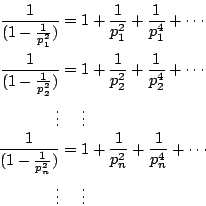
�N�U���ۭ��]�A�[�H�����������^�o��q���� 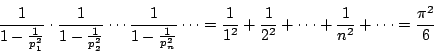
�˼Ʊo
|
��~�j�M����r�G �DEuler �DBernoulli �D�f�V�Q�ż� �DDe Moivre |
|
|
|
|
�]�Y�������B�ðݡK�K�A�i�H�b�� �d�� �� �g�H ���ڭ̡C�^ |
|
|
|
EpisteMath (c) 2000 ������s�|�ƾǩҡB�x�j�ƾǨt �U�����峹���e���ۧ@�v����ۧ@�H�Ҧ� |
| �s��G�x�� | �̫�ק����G4/26/2002 |