四、空間中的平行與垂直 (第 2 頁)

　1│2　

《基礎幾何學》

四、空間中的平行與垂直
——平直性與對稱性的交互作用（第 2 頁）

項武義

首頁 | 搜尋

．作者任教於香港科技大學數學系
‧對外搜尋關鍵字

對稱性與垂直

垂直平分線與平面上的反射對稱

讓我們先來溫習一下平面的情形：

$\bullet$

平面中和給定兩點 A, B 等距的點集（亦稱之為軌跡）是 $\overline{AB}$ 的垂直平分線

$\begin{displaymath} \begin{xy} \xyimport(5,5){\epsfxsize =5cm \epsfbox{fig0406.e... ...B} ,(2.75,2.2)*+{M} ,(2.7,4.8)*+{P} ,(2.7,0.2)*+{\ell} \end{xy}\end{displaymath}$

[ 圖 4-6 ]

$\bullet$

平面對于其中一條給定直線 $\ell$ 成反射對稱；P, P' 對于 $\ell$ 互為對稱點的充要條件是 $\overline{PP'}$ 被 $\ell$ 所垂直平分或 $P=P'\in \ell$ （如 [圖 4-7] 所示，試証 $\overline{PQ}$ 和 $\overline{P'Q'}$ 恆為等長。）

$\begin{displaymath} \begin{xy} \xyimport(5,5){\epsfxsize =5cm \epsfbox{fig0407.e... ...3)*+{\scriptstyle A=A'} ,(4.4,4.9)*+{Q} ,(4.4,0)*+{Q'} \end{xy}\end{displaymath}$

[ 圖 4-7 ]

【習題】：

$\begin{displaymath} \begin{xy} \xyimport(5,5){\epsfxsize =7cm \epsfbox{fig0408.e... ...7)*+{ \nu} ,(3.55,2.75)*+{ \nu} ,(3.2,2.7)*+{ \lambda} \end{xy}\end{displaymath}$

[ 圖 4-8 ]

如 [圖 4-8] 所示，設 A 是 $\ell$ 上的任給一點，λ 和 ν 是 $\overline{PA}$ 和 $\overline{AQ}$ 與 $\ell$ 的垂線之間的夾角。試証 $\overline{PA}+\overline{AQ}$ 在 $\lambda=\nu$ 時為極小（亦即 $\overline{QA_0}$ 的延長線過 P 的對稱點 P' 者）。

上述平面上的反射對稱和垂直平分線之間的簡潔關係在空間的推廣乃是立體幾何極為基本的要點。首先，我們要研討空間之中和給定兩點 A, B 等距的點集，即

【定理 4.3】：設 A, B 是給定相異兩點， $\cal S$ 是空間中所有和 A, B 等距的點所構成者。則 $\cal S$ 是一個過 $\overline{AB}$ 中點 M 的平面，而且 $\cal S$ 上任何過 M 點的直線都和 $\overline{AB}$ 垂直（亦稱正交）。

[一個簡約的描述是： $\cal S$ 乃是直線段 $\overline{AB}$ 的垂直平分面。]

証明：論証的要點在于証明 $\cal S$ 的平直性。設 P₁, P₂ 是 $\cal S$ 之中的相異兩點，而 P 是直線 P₁P₂ 上任給一點。我們所要証者是 P 點也必然屬于 $\cal S$ ，亦即由所設

$\begin{displaymath} \overline{AP_1}=\overline{BP_1},\quad \overline{AP_2}=\overline{BP_2}, %% \quad P\in P_1P_2 \end{displaymath}$

推論 $\overline{AP}=\overline{BP}$ 。茲証之如下：

由所設 $\bigtriangleup AP_1P_2$ 和 $\bigtriangleup BP_1P_2$ 滿足 S.S.S. 全等條件，所以

$\begin{displaymath} \angle PP_1A=\angle PP_1B,\quad \angle PP_2A=\angle PP_2B \end{displaymath}$

由此可見， $\bigtriangleup PP_1A$ 和 $\bigtriangleup PP_1B$ 滿足 S.A.S. 全等條件，即有 $\bigtriangleup PP_1A \cong \bigtriangleup PP_1B$ ，所以 $\overline{AP}=\overline{BP}$ 。（同理也有 $\bigtriangleup PP_2A \cong \bigtriangleup PP_2B$ ，但只用其一已經証得 $\overline{AP}=\overline{BP}$ 。）所以 $\cal S$ 是一個平直子集，它顯然包含 $\overline{AB}$ 的中點 M，但不是包含 A, B。而且對于任給一個 $\cal S$ 中相異于 M 的點 P， ${\cal S}\,\cap <\!\!\{A,B,P\}\!\!>$ 等于平面 $<\!\!\{A,B,P\}\!\!>$ 中 $\overline{AB}$ 的垂直平分線，所以 $\cal S$ 必定是一個平面。它其實是由所有這種垂直平分線所組合成者（參看 [圖 4-9]）。 □

$\begin{displaymath} \begin{xy} \xyimport(5,5){\epsfxsize =7cm \epsfbox{fig0409.e... ...\cal S} ,(2.3,2.7)*+{M} ,(1,1.4)*+{P} ,(2.5,-0.2)*+{B} \end{xy}\end{displaymath}$

[ 圖 4-9 ]

【推論】：設 $\ell\cap\Pi=\{M\}$ ，而且 $\ell$ 和 Π 上兩條相異的 MP₁, MP₂ 正交，則 $\ell$ 和 Π 上任給過 M 點的直線皆正交。

証明：在直線 $\ell$ 上任取一直線段 $\overline{AB}$ 以 M 為其中點，令 $\cal S$ 為 $\overline{AB}$ 的垂直平分面。由所設 M, P₁, P₂ 是 $\cal S$ 和 Π 上不共線三點。所以 ${\cal S}=\Pi$ 。

【線、面垂直之定義】：若 $\ell\cap\Pi=\{M\}$ 而且 $\ell$ 和 Π 上所有過 M 點的直線皆為正交，則稱 $\ell$ 垂直于 Π，以 $\ell \perp \Pi$ 記之。

[上述推論則說，只要檢驗其中兩條在 Π 上過交點 M 和 $\ell$ 的正交性，即可得知 $\ell \perp \Pi$ 。]

立體幾何中的作圖題

在討論立體幾何的作圖題之前，讓我們先分析一下它和平面幾何的作圖題在實踐上的基本差別：

(i): 一張紙、一塊黑板都是一個平面的局部，因此常用的平面幾何作圖是真的可以在一張紙或黑板上逐步用直尺、圓規去畫出來的。但是立體幾何的作圖所要用到的是 3-維的「紙」或「黑板」才能實地執行之。而這種 3-維的「紙」和「黑板」是不實用而且難以供應的。
(ii): 在平面幾何作圖中，可以用直尺去畫出紙上兩點所決定的那條直線的局部，但是在立體幾何作圖中並沒有一個簡單的工具能夠利落簡潔地畫出不共線三點所決定的那個平面的局部。
(iii): 由此可見，立體幾何作圖在本質上乃是「理念作圖」。我們真正所要做的是把某種唯一存在、簡單而且基本的立體幾何事物，在理念中逐步分解成某些特定的平面上的平面幾何作圖的組合而加以明確的刻劃。這種理念作圖在訓練如何把立體幾何中的基本圖象歸于平面幾何作圖來加以分析。唯有通過這種理念作圖的練習，才能學會如何有效運用平面幾何所學者去進而理解空間的本質。我們與生俱來的視覺是具有相當好的空間想象能力的，但是要把它提升到對于空間圖象及其所蘊含的空間本質的洞察力，這種訓練是不可缺的！
[例如在 [定理 4.2] 的存在性的証明中，所做的就是這種理念作圖。]

【基本作圖題 4.1】：過直線 $\ell$ 上的給定點 M ，作其垂面。

作法：在 $\ell$ 外取兩點 P₁, P₂ 使得

$\begin{displaymath} \Pi_1=<\!\!\ell\cup \{P_1\}\!\!>\; \hbox{{\fontfamily{cwM0}\... ...font \cH230}{\fontfamily{cwM0}\fontseries{m}\selectfont \cH1}} \end{displaymath}$

用平面幾何基本作圖分別作 $\Pi_1$ 和 $\Pi_2$ 中過 M 點而且和 $\ell$ 垂直的直線 $\ell_1$ , $\ell_2$ 。則 $\Pi=<\!\!\ell_1\cup\ell_2\!\!>$ 即為所求作的垂面。 [証明留作習題]

【基本作圖題 4.2】：過平面 Π 上一點 P，作其垂線。

作法：在 Π 上任取一條過 P 點的直線 $\ell$ 。過 P 點用[基本作圖 4.1]作 $\ell$ 的垂面 $\Pi_1$ 。令 $\ell_1=\Pi_1\cap\Pi$ ，再在 $\Pi_1$ 中作過 P 點而且垂直于 $\ell_1$ 的直線，即為所求作的直線。 [証明留作習題]

【基本作圖題 4.3】：設 P 是平面 Π 之外的給定點。求作過 P 點而且垂直于 Π 的直線。

作法：先在 Π 上任取一點 Q。用[基本作圖 4.2]作和 Π 正交于 Q 的直線 $\ell_1$ 。若 $\ell_1$ 恰好也過 P 點，則 $\ell_1$ 即為所求作者。不然，令 $\Pi_1=<\!\!\{P\}\cup \ell_1\!\!>$ ，再用平面幾何基本作圖在平面 $\Pi_1$ 中作過 P 點而且和 $\ell_1$ 平行的直線 $\ell(P)$ ，則 $\ell(P)$ 即為所求作的垂線。 [証明留作習題]

在平面幾何中，一個角區的邊界由兩條共頂點的半線（亦即射線）所組成。相類似地，空間的一個兩面角區的邊界是由兩個共頂棱的半平面所組成（參看 [圖 4-10]）。

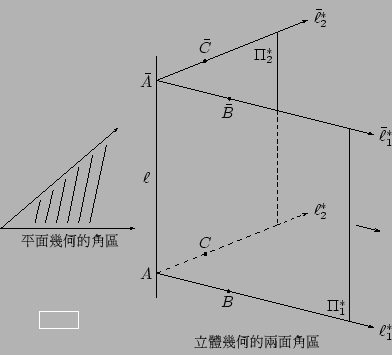
$\begin{displaymath} \begin{xy} \xyimport(5,5){\epsfxsize =3cm \epsfbox{fig0410a.... ...z{\fontfamily{cwM0}\fontseries{m}\selectfont \cH150}}} \end{xy}\end{displaymath}$

[ 圖 4-10 ]

【引理 4.3】：如 [圖 4-10] 所示，設 A, 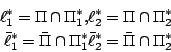$\bar{A}$ 是 $\ell$ 上任取兩點。Π, $\bar{\Pi}$ 分別是過 A, $\bar{A}$ 而且和 $\ell$ 正交的平面。令

$\begin{eqnarray*} \ell^*_1=\Pi\cap\Pi^*_1, && \ell^*_2=\Pi\cap\Pi^*_2 \\ \bar{\... ...=\bar{\Pi}\cap\Pi^*_1 %% && \bar{\ell}^*_2=\bar{\Pi}\cap\Pi^*_2 \end{eqnarray*}$

則有 $\angle \ell^*_1,\ell^*_2)=\angle \bar{\ell}^*_1,\bar{\ell}^*_2)$ 。

証明：如 [圖 4-10] 所示，在射線 $\ell^*_1$ , $\ell^*_2$ , $\bar{\ell}^*_1$ , $\bar{\ell}^*_2$ 上分別取 B, C, $\bar{B}$ , $\bar{C}$ 使得 $\overline{AB}=\overline{\bar{A}\bar{B}}$ , $\overline{AC}=\overline{\bar{A}\bar{C}}$ 。由所作易見 $\overline{AB}$ 和 $\overline{\bar{A}\bar{B}}$ ； $\overline{AC}$ 和 $\overline{\bar{A}\bar{C}}$ 皆為同向平行而且等長。再由[定理 4.2]的推論即有 $\overline{BC}$ 和 $\overline{\bar{B}\bar{C}}$ 也是同向平行而且等長的。所以 $\bigtriangleup ABC$ 和 $\bigtriangleup \bar{A}\bar{B}\bar{C}$ 滿足 S.S.S. 全等條件， $\angle \ell^*_1,\ell^*_2)=\angle A=\angle \bar{A}=\angle \bar{\ell}^*_1,\bar{\ell}^*_2)$ 。 □

【兩面角的定義】： $\angle \Pi^*_1,\Pi^*_2)$ 的大小定義為 $\angle \ell^*_1,\ell^*_2)$ ，因為後者是和 $\ell$ 上 A 點的選取無關的！再者，在 $\angle \Pi^*_1,\Pi^*_2)=\displaystyle\frac{\pi}{2}$ 時，則稱兩面正交，以符號 $\Pi_1\perp\Pi_2$ 記之。

【基本作圖題 4.4】：設 $\ell\subset\Pi$ , ${\mathfrak U}^*_\Pi$ 是以平面 Π 為邊界的半空間， $\Pi^*_\ell$ 是 Π 中以 $\ell$ 為邊界的半平面。求作 ${\mathfrak U}^*_\Pi$ 中那個和 $\Pi^*_\ell$ 共以 $\ell$ 為頂棱的半平面 $\bar{\Pi}^*_\ell$ ，使得 $\angle \Pi^*_\ell, \bar{\Pi}^*_\ell)$ 等于一個給定角。

作法：在 $\ell$ 上任取一點 A，過 A 點作 $\ell$ 的垂面 $\Pi_1$ ，令 $\ell^*_1=\Pi_1\cap\Pi^*_\ell$ 。再用平面幾何基本作圖在 $\Pi_1$ 中的半面 $\Pi_1\cap{\mathfrak U}^*_\Pi$ 中作那條半線 $\ell^*_2$ 使得 $\angle \ell^*_1,\ell^*_2)$ 等于給定角。則 $<\!\!\ell\cup \ell^*_2\!\!>\cap \,{\mathfrak U}^*_\Pi$ 就是所求作者。 [由上述定義，可見証明是顯然的。]

【引理 4.4】：設 $\ell_1\perp\Pi$ , $\ell_2\perp\Pi$ ，則 $\ell_1 /\!/ \ell_2$ 。

証明：令 $P_1=\ell_1\cap\Pi$ , $P_2=\ell_2\cap\Pi$ 。若 P₁=P₂，則 $\ell_1=\ell_2$ 。若 $P_1\neq P_2$ ，令 $\Pi'=<\!\!\ell_1\cup \{P_2\}\!\!>$ , $\ell'_2$ 是 $\Pi'$ 中過 P₂ 點而且和 $\ell_1$ 平行的直線。由 $\ell_1\perp\Pi$ 可見 $\angle \Pi,\Pi')=\displaystyle\frac{\pi}{2}$ 。再由[引理 4.3]，可証 $\ell'_2\perp\Pi$ 。所以 $\ell'_2=\ell_2$ ，亦即 $\ell_1 /\!/ \ell_2$ （參看 [圖 4-11]）。

$\begin{displaymath} \begin{xy} \xyimport(5,5){\epsfxsize =6cm \epsfbox{fig0411.e... ...5,1.9)*+{P_2} ,(3.45,4.8)*+{\ell_2} ,(4.65,3.1)*+{\Pi} \end{xy}\end{displaymath}$

[ 圖 4-11 ]

【習題】：

(1)

証明[基本作圖 4.1]的作法所得者乃是唯一合乎所求作的條件者。

(2)

証明[基本作圖 4.2]的作法所得者乃是唯一合乎所求作的條件者。

(3)

証明[基本作圖 4.3]的作法所得者乃是唯一合乎所求作的條件者。

(4)

設 $\Pi\perp\ell$ , $\Pi'\perp\ell$ ，則 $\Pi /\!/ \Pi'$ 。試証之。

(5)

設 $\Pi\perp\ell$ 而且 $\Pi /\!/ \Pi'$ ，則 $\ell\perp\Pi'$ 。試証之。

(6)

設 $\ell_1\perp\Pi$ , $\ell_1 /\!/ \ell_2$ ，則 $\ell_2\perp\Pi$ 。試証之。

(7)

設 $\ell_1\cap\ell_2=\{P\}$ 而且 $\ell_1 /\!/ \Pi$ , $\ell_2 /\!/ \Pi$ ，則 $<\!\!\ell_1\cup \ell_2\!\!> /\!/ \Pi$ 。試証之。

(8)

設 $\ell\perp\Pi, \;\Pi'\supset \ell$ ，則 $\Pi'\perp\Pi$ 。試証之。

(9)

設 $\Pi_1\cap\Pi_2=\ell$ , $\Pi_1\perp\Pi,\;\Pi_2\perp\Pi$ ，則 $\ell \perp \Pi$ 。試証之。

(10)

設 $\Pi_1\cap\Pi_2=\phi$ , $\ell_1,\ell_2$ 是兩條垂直于 $\Pi_1,\Pi_2$ 的直線。令 $P_1=\ell_1\cap\Pi_1$ , $P_2=\ell_1\cap\Pi_2$ , $Q_1=\ell_2\cap\Pi_1$ , $Q_2=\ell_2\cap\Pi_2$ ，試証 $\overline{Q_1Q_2}$ 和 $\overline{P_1P_2}$ 等長。

[上述和公垂線選取無關的長度，將定義為 $\Pi_1$ , $\Pi_2$ 這一對平行面之間的距離，將以符號 $d\big(\Pi_1,\Pi_2)$ 記之。]

(11)

如 [圖 4-12] 所示，PM 和 Π 正交于 M, $\ell\subset\Pi$ ，MN 和 $\ell$ 正交于 N，則 PN 和 $\ell$ 正交。試証之。

$\begin{displaymath} \begin{xy} \xyimport(5,5){\epsfxsize =5cm \epsfbox{fig0412.e... ....95,1.65)*+{N} ,(3.5,0.65)*+{\ell} ,(4.65,2.85)*+{\Pi} \end{xy}\end{displaymath}$

[ 圖 4-12 ]

[提示：要點在于証明 $<\!\!\{P,M,N\}\!\!>$ 和 $\ell$ 是正交的。]

(12)

【基本作圖題 4.5】過直線 $\ell$ 之外一點 P 作其垂面 $\Pi(P)$ 。

空間反射對稱性與垂直投影

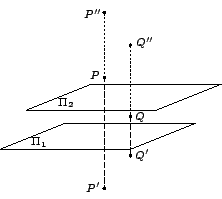
對于空間中一個給定平面 Π，每個點 P 有一個唯一的對稱點 P' 。若 $P\in \Pi$ 則其對稱點 P' 就是 P 本身。若 $P\notin \Pi$ ，則 $\overline{PP'}$ 以 Π 為其垂直平分面，如 [圖 4-13] 所示。易見 P 也就是 P' 的對稱點。

$\begin{displaymath} \begin{xy} \xyimport(5,5){\epsfxsize =5cm \epsfbox{fig0413.e... ...} ,(2.6,2.4)*+{M} ,(2.05,0.1)*+{P'} ,(3.95,1.2)*+{\Pi} \end{xy}\end{displaymath}$

[ 圖 4-13 ]

【定義】：上述空間中 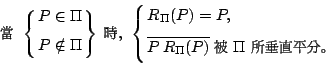$P\mapsto P'$ 這個變換 (transformation) 叫做空間對于給定平面 Π 的反射對稱，將以符號 ${\mathfrak R}_\Pi$ 記之，亦即

$\begin{displaymath} \hbox{{\fontfamily{cwM1}\fontseries{m}\selectfont \cH231} } ... ...cwM0}\fontseries{m}\selectfont \cH1}} \\ \end{eqalign}\right. \end{displaymath}$

顯然有 ${\mathfrak R}_\Pi\big({\mathfrak R}_\Pi(P)\big)=P$ 恆成立，亦即 ${\mathfrak R}^2_\Pi$ 乃是空間的恆等變換。

【定理 4.4】： ${\mathfrak R}_\Pi$ 是空間的一個保長變換，亦即直線段 $\overline{PQ}$ 和 $\overline{{\mathfrak R}_\Pi(P)\,{\mathfrak R}_\Pi(Q)}$ 恆為等長。

証明：在此我們採用簡約符號 P' 表示 ${\mathfrak R}_\Pi(P)$ ，而且把証明分為下述四種情形：

(i)

若 $P,Q\in \Pi$ 時，P'=P, Q'=Q。 $\overline{P'Q'}$ 就是 $\overline{PQ}$ 本身。

(ii)

若 P, Q 中其一個屬于 Π，設其為 P。則 P'=P，而 $\overline{QQ'}$ 被 Π 所垂直平分。所以 $\bigtriangleup PQQ'$ 的中線 $\overline{PM}$ 和底邊 $\overline{QQ'}$ 正交，亦即 $\bigtriangleup PQQ'$ 是等腰三角形，即已証得 $\overline{PQ}=\overline{PQ'}=\overline{P'Q'}$ 。

(iii)

若 $PQ\cap\Pi=\phi$ ，令 $\overline{PP'}$ 和 $\overline{QQ'}$ 的中點分別為 M, N。則易証 $\Box PMNQ$ 和 $\Box P'MNQ'$ 都是矩形，所以即有 $\overline{PQ}=\overline{MN}=\overline{P'Q'}$ 。

(iv)

若 $PQ\cap \Pi=\{A\}$ ，則 (ii) 之所証可見 $\bigtriangleup APP'$ 和 $\bigtriangleup AQQ'$ 都是等腰的，亦即

$\begin{displaymath} \overline{AP}=\overline{AP'},\quad \overline{AQ}=\overline{A... ...ad \Rightarrow \quad \overline{PQ}=\overline{P'Q'} \eqno \Box \end{displaymath}$

[註]：保長變換的組合當然還是保長變換。現在讓我們來分析一下，對于兩個（相異的）平面 $\Pi_1$ , $\Pi_2$ 的反射對稱的組合 ${\mathfrak R}_{\Pi_2}\circ {\mathfrak R}_{\Pi_1}(P)=%% {\mathfrak R}_{\Pi_2}\big({\mathfrak R}_{\Pi_1}(P)\big)$ 究竟是一種怎樣的保長變換。為此，我們將採用簡約符號

$\begin{displaymath} P'={\mathfrak R}_{\Pi_1}(P),\quad P''={\mathfrak R}_{\Pi_2}(P')=%% {\mathfrak R}_{\Pi_2}\circ {\mathfrak R}_{\Pi_1}(P) \end{displaymath}$

下面將分成 $\Pi_1\cap\Pi_2=\phi$ 和 $\Pi_1\cap\Pi_2=\ell$ 這兩種情形來加以分析：

情況一： ${\Pi_1\cap\Pi_2=\phi}$ （亦即 $\Pi_1 /\!/ \Pi_2$ ）

令 $\ell(P)$ 是過 P 點而且和 $\Pi_1$ , $\Pi_2$ 正交的直線，易見 P', P'' 點都在 $\ell(P)$ 上。令 $Q_1=\ell(P)\cap\Pi_1$ , $Q_2=\ell(P)\cap\Pi_2$ ，並以 $\overrightarrow{Q_1Q_2}$ 為 $\ell(P)$ 上的正向，則有下述有向長度關係式，即

$\begin{displaymath} \overrightarrow{PQ_1}=\overrightarrow{Q_1P'},\quad %% \over... ...rrow{Q_1P'}+\overrightarrow{P'Q_2}=%% \overrightarrow{Q_1Q_2} \end{displaymath}$

所以

$\begin{displaymath} \overrightarrow{PP''}=%% \overrightarrow{PP'}+\overrightarr... ..._1P'}+2\,\overrightarrow{P'Q_2}=%% 2\,\overrightarrow{Q_1Q_2} \end{displaymath}$

我們把上述分析之所得敘述為[定理 4.5]：

【定理 4.5】：設 $\Pi_1\cap\Pi_2=\phi$ ，則 ${\mathfrak R}_{\Pi_2}\circ {\mathfrak R}_{\Pi_1}$ 把空間中每一點 P 沿著垂直于 $\Pi_1$ , $\Pi_2$ 的方向（亦即同向平行于 $\overrightarrow{Q_1Q_2}$ 者）向前移動 $2d\big(\Pi_1,\Pi_2\big)$ 。

[這種保長變換叫做平移 (translation)。]

$\begin{displaymath} \xy \xyimport(5,5){\epsfysize=4cm \epsfbox{fig0414.eps}}*\fr... ....2,1)*+{\scriptstyle Q'} ,(3.25,4.1)*+{\scriptstyle Q''} \endxy\end{displaymath}$

[ 圖 4-14 ]

情況二： ${\Pi_1\cap\Pi_2=\ell}$ （相交于直線 $\ell$ ）

令 $\Pi(P)$ 是過 P 點而且和 $\ell$ 垂直的平面（[基本作圖 4.5]，亦即習題 (12)），則 $\Pi(P)\perp\Pi_1$ , $\Pi(P)\perp\Pi_2$ 。由此易証 P' 和 P'' 點都和 P 點共在 $\Pi(P)$ 之中（証明留作習題）。令 $\ell_1=\Pi(P)\cap\Pi_1$ , $\ell_2=\Pi(P)\cap\Pi_2$ , $A=\ell\cap\Pi(P)$ 。在 $\Pi(P)$ 上選取正向轉角使得

$\begin{displaymath} 0<\angle\Pi_1,\Pi_2)=\angle\ell_1,\ell_2)\leq \frac{\pi}{2} \end{displaymath}$

則有下述 $\Pi(P)$ 中定向角的關係式，即如 [圖 4-15] 所示

$\begin{displaymath} \angle PAM_1=\angle M_1AP',\quad \angle P'AM_2=\angle M_2AP'' \end{displaymath}$

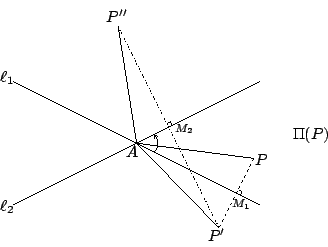
$\begin{displaymath} \begin{xy} \xyimport(5,5){\epsfxsize =5.5cm \epsfbox{fig0415... ...7)*+{\ell_1} ,(-0.1,0.55)*+{\ell_2} ,(6,2.3)*+{\Pi(P)} \end{xy}\end{displaymath}$

[ 圖 4-15 ]

所以

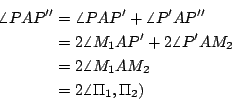
$\begin{eqnarray*} \angle PAP'' &=& \angle PAP'+\angle P'AP'' \\ &=& 2\angle M_1... ...ngle P'AM_2 \\ &=& 2\angle M_1AM_2 \\ &=& 2\angle \Pi_1,\Pi_2) \end{eqnarray*}$

上述分析已經証得下述定理，即

【定理 4.6】：設 $\Pi_1\cap\Pi_2=\ell$ , $\theta=\angle \Pi_1,\Pi_2)$ ，則 ${\mathfrak R}_{\Pi_2}\circ {\mathfrak R}_{\Pi_1}$ 保持任何一個 $\ell$ 的垂面 $\Pi(P)$ 為不變子集 (invariant subset)，而 $\ell$ 本身則是它的定點子集 (subset of fixed points)。再者，把 ${\mathfrak R}_{\Pi_2}\circ {\mathfrak R}_{\Pi_1}$ 限制到任一不變平面 $\Pi(P)$ 上的作用乃是一個 2θ-角的旋轉 (rotation)。

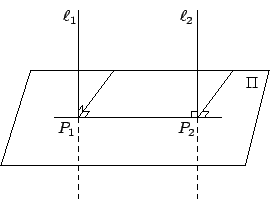
[這種保長變換叫做空間繞 $\ell$ -軸的旋轉。]

垂直投影 (orthogonal projection)：

對于空間中一個給定平面 Π，過每一點 P 可作唯一一條直線 $\ell(P)$ 和 Π 正交。對于空間一條給定直線 $\ell$ ，過每一點 P 可作唯一一個平面 $\Pi(P)$ 和 $\ell$ 正交。運用上述兩個事實就可以定義空間的兩種垂直投影：

【定義】：空間對于一個給定平面 Π 的垂直投影把 P 點映射到 $\ell(P)\cap\Pi$ 。由此可見，它把每條垂直于 Π 的直線上的所有點都映射到該直線和 Π 的交點，將以符號 ${\mathfrak P}_\Pi$ 記之。

$\begin{displaymath} \xy \xyimport(5,5){\epsfxsize=7cm \epsfbox{fig0416.eps}}*\fr... ...} ,(3.8,1.5)*+{C'} ,(1.85,1.5)*+{D'} ,(0.45,0.35)*+{\Pi} \endxy\end{displaymath}$

[ 圖 4-16 ]

【定義】：空間對于一個給定直線 $\ell$ 的垂直投影把 P 點映射到 $\Pi(P)\cap\ell$ 。由此可見，它把每個和 $\ell$ 垂直的平面上的所有點，全都映射到它和 $\ell$ 的交點，將以 ${\mathfrak P}_\ell$ 記之。

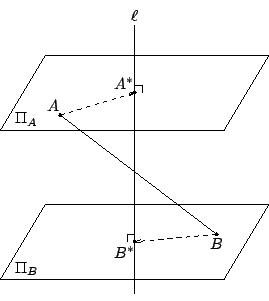
$\begin{displaymath} \xy \xyimport(5,5){\epsfxsize=6cm \epsfbox{fig0417.eps}}*\fr... ...^*} ,(4,0.95)*+{B} ,(2.3,0.8)*+{B^*} ,(0.5,0.5)*+{\Pi_B} \endxy\end{displaymath}$

[ 圖 4-17 ]

【定理 4.7】：以簡約符號 P' 表示 ${\mathfrak P}_\Pi(P)$ 。設 $P'\neq Q'$ ，則有 $X\in PQ \Rightarrow X'\in P'Q'$ 而且

$\begin{displaymath} \frac{\overrightarrow{PX}}{\;\overrightarrow{XQ}\;}=%% \fra... ... \cH243}\z{\fontfamily{cwM2}\fontseries{m}\selectfont \cH16})} \end{displaymath}$

証明：令 $\Pi_1=<\!\!\ell(P)\cup \ell(Q)\!\!>$ , $\big(\ell(P) /\!/ \ell(Q)\big)$ 。由所設

$\begin{displaymath} X\in PQ \;\hbox{ {\fontfamily{cwM0}\fontseries{m}\selectfont... ...) /\!/ \ell(Q)%% \quad \Rightarrow \quad \ell(X)\subset \Pi_1 \end{displaymath}$

由此可見 $X'\in P'Q'$ （整個 $\Pi_1$ 在 ${\mathfrak P}_\Pi$ 下的象點點集）。

$\begin{displaymath} \begin{xy} \xyimport(5,5){\epsfxsize =6cm \epsfbox{fig0418.e... ...*+{\ell(P)} ,(1.9,-0.3)*+{\ell(X)} ,(6,1.2)*+{(\Pi_1)} \end{xy}\end{displaymath}$

[ 圖 4-18 ]

再者，如 [圖 4-18] 所示和平面幾何中的相似三角形定理，即得

$\begin{displaymath} \frac{\overrightarrow{PX}}{\;\overrightarrow{XQ}\;}=%% \fra... ...c{\overrightarrow{P'X'}}{\;\overrightarrow{X'Q'}\;} \eqno \Box \end{displaymath}$

【推論】：若 $\hskip-3pt\raise-1pt\hbox{\xy\xyimport(1,1){\epsfxsize=0.6cm \epsfbox{pgram.eps}}*\frm{} \endxy }\hskip-1ptABCD$ 是一個平行四邊形而且 A', B', C', D' 不共線，則 $\hskip-3pt\raise-1pt\hbox{\xy\xyimport(1,1){\epsfxsize=0.6cm \epsfbox{pgram.eps}}*\frm{} \endxy }\hskip-1ptA'B'C'D'$ 也是一個平行四邊形（見 [圖 4-16]）。

証明：由所設 $\overline{AC}$ 和 $\overline{BD}$ 互相平分。由[定理 4.7]，即得 $\overline{A'C'}$ 和 $\overline{B'D'}$ 也互相平分，所以 $\hskip-3pt\raise-1pt\hbox{\xy\xyimport(1,1){\epsfxsize=0.6cm \epsfbox{pgram.eps}}*\frm{} \endxy }\hskip-1ptA'B'C'D'$ 也是一個平行四邊形。 □

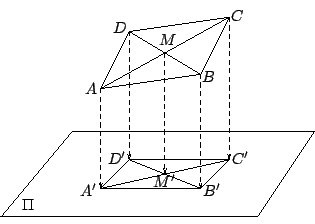
【定理 4.8】：以簡約符號 P^* 表示 ${\mathfrak P}_\ell(P)$ 。設 $P^*\neq Q^*$ , $X\in PQ$ ，則同樣地也有

$\begin{displaymath} \frac{\overrightarrow{PX}}{\;\overrightarrow{XQ}\;} = \frac{\overrightarrow{P^*X^*}}{\;\overrightarrow{X^*Q^*}\;} \end{displaymath}$

証明：過 P 點作 $\ell$ 的平行線 $\ell'$ 。則 $\ell'$ 和 $\Pi(P)$ , $\Pi(Q)$ , $\Pi(X)$ 也都是正交的。令

$\begin{displaymath} \Pi_1=<\!\!PQ\cup\ell'\!\!>,\; X_1=\ell'\cap\Pi(X),\; Q_1=\ell'\cap\Pi(Q) \end{displaymath}$

則易見

$\begin{displaymath} \overrightarrow{P^*X^*}=\overrightarrow{PX_1},\quad %% \overrightarrow{X^*Q^*}=\overrightarrow{X_1Q_1} \end{displaymath}$

而同樣的圖形和相似三角形定理即得

$\begin{displaymath} \frac{\overrightarrow{PX}}{\;\overrightarrow{XQ}\;}=%% \fra... ...verrightarrow{P^*X^*}}{\;\overrightarrow{X^*Q^*}\;} \eqno \Box \end{displaymath}$

【定理 4.9】：設 $\{\ell_1,\ell_2,\ell_3\}$ 是共交于一點 O 而且兩兩正交的三條直線。若以簡約符號 P_i 表示 ${\mathfrak P}_{\ell_i}(P)$ 則有

$\begin{displaymath} \overline{PQ}^2=\overline{P_1Q_1}^2+\overline{P_2Q_2}^2+%% \overline{P_3Q_3}^2 \end{displaymath}$

[這也就是勾股定理在空間幾何中的表達式]

証明：令 Π 是過 P 點和 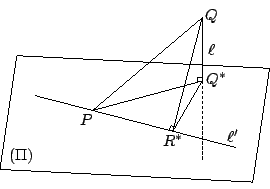$\ell_3$ 正交的平面， $\ell$ 是過 Q 點和 $\ell_3$ 平行的直線， $\ell'$ 是過 P 點而且和 $\ell_1$ 平行的直線。如 [圖 4-19] 所示，令 $Q^*=\ell\cap\Pi$ ，並作 Q^*R^* 和 $\ell'$ 正交于 R^* 則有

$\begin{displaymath} \overline{QQ^*}\perp\overline{PQ^*} \; %% \hbox{({\fontfami... ...tfont \cH127}}\;\overline{QQ^*}\perp\overline{R^*Q^*} \hbox{)} \end{displaymath}$

$\begin{displaymath} \begin{xy} \xyimport(5,5){\epsfxsize =6cm \epsfbox{fig0419.e... ...3.9,4)*+{\ell} ,(4.3,1.4)*+{\ell'} ,(0.4,0.8)*+{(\Pi)} \end{xy}\end{displaymath}$

[ 圖 4-19 ]

所以由勾股定理即有

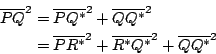
$\begin{eqnarray*} \overline{PQ}^2 &=& \overline{PQ^*}^2+\overline{QQ^*}^2 \\ &=& \overline{PR^*}^2+\overline{R^*Q^*}^2+\overline{QQ^*}^2 \end{eqnarray*}$

再者，由所作易見

$\begin{displaymath} \overline{PR^*}=\overline{P_1Q_1},\quad %% \overline{R^*Q^*}=\overline{P_2Q_2},\quad %% \overline{QQ^*}=\overline{P_3Q_3} \end{displaymath}$

所以即已証得

$\begin{displaymath} \overline{PQ}^2=\overline{P_1Q_1}^2+\overline{P_2Q_2}^2+%% \overline{P_3Q_3}^2 \eqno \Box \end{displaymath}$

【習題】：

光的反射定律：一個平滑的鏡面可以想成是一個平面的局部。遠在古希臘時代，即已認識到下述光的反射定律：

「入射線、反射線和平面在反射點的法線三線共面，而且兩者和法線的夾角相等。」

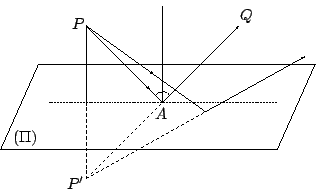
$\begin{displaymath} \begin{xy} \xyimport(5,5){\epsfxsize =7cm \epsfbox{fig0420.e... ...} ,(3.9,4.7)*+{Q} ,(2.55,1.9)*+{A} ,(0.4,1.2)*+{(\Pi)} \end{xy}\end{displaymath}$

[ 圖 4-20 ]

(1): 令 P' 是 P 對于鏡面 Π 的反射對稱點。試証起始于 P 點的反射線的延長線共交于 P' 點。 [這也就是視覺中鏡象的幾何原由。]
(2): 如 [圖 4-20] 所示，起始于 P 點的光線，先走直線到達鏡面 Π 上一點 A 然後再反射到 Q 點。試証這種走法是由 P 點經過 Π 上一點然後再到 Q 點的唯一最短通路。（亦即其他經過 Π 上一點由 P 到 Q 的通路都比 $\overline{PA}+\overline{AQ}$ 要長！）
(3): 設 $\Pi_1,\Pi_2,\Pi_3$ 是共交于 O 點而且兩兩垂直的三個平面。令 $P^\char93 ={\mathfrak R}_{\Pi_3}\circ{\mathfrak R}_{\Pi_2}%% \circ{\mathfrak R}_{\Pi_1}(P)$ 。試問 P, O, P# 三點的幾何關係是什麼？

設 T 是空間的一個保長變換（例如是好些個反射對稱的組合），並且用簡約符號 $\widehat{P}$ 記號 T(P)。

(4): 試証 $X\in \overline{PQ} \Rightarrow \widehat{X} %% \in \overline{\widehat{P}\widehat{Q}}$ 。
(5): 設 $\bigtriangleup PQR$ 為直角三角形，試証 $\bigtriangleup \widehat{P}\widehat{Q}\widehat{R}$ 也是一個直角三角形。
(6): 試証 $\bigtriangleup PQR$ 和 $\bigtriangleup \widehat{P}\widehat{Q}\widehat{R}$ 必定是全等的。
(7): 設 A, B 是空間任給兩點，是否存在一個適當的平移 T 使得 T(A)=B？試用反射對稱之組合構造之。
(8): 上述平移是否是唯一存在的？試証明你的觀點。

　1│2　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

最後修改日期：6/19/2004