科學哲學家馬赫說：「你無法了解一個理論，除非你知道它是如何發現的。」打從27年前《科學月刊》創刊（民國59年元月）開始，曹亮吉教授（筆名阿草）就懷著一股熱情，不斷地為《科學月刊》寫稿，致力於數學通識教育，傳播和普及數學知識。最難能可貴的是，他持之以恒，歷久不衰。
對於數學的學習，發現與證明兼備才算完全。
後來，他逐次將文章集結，或整理，或改寫，於是產生下列各著作：
- 《談數學》（民69年，科學出版事業基金會）
- 《益智集》（民69年，科學出版事業基金會）
- 《微積分史話》（民69年，科學出版事業基金會）
- 《數學導論》（民77年，科學月刊社）
- 《微積分》（民79年，歐亞書局）
去年八月更出版：
- 《阿草的葫蘆》（民85年，遠哲科學教育基金會）
這本書是擷取先前工作的精華，經過增補和千錘百鍊得來的， 所以可讀性與趣味性更高。數學通識教材又增添一重要的文獻。 寫一本書所費的勞力與腦力，相當於蓋一棟大廈，我們欣見且敬佩阿草的努力成果， 為台灣的數學教育注入一股清新的活力。
數學是人類文明的一個重要因素，在西方文明中，更占有核心的地位，所以通識教育不能缺少數學，這大家都沒有異議。如何選材，如何舖陳內容，這就見仁見智了。正如好的教學可以有各種不同的風格與魅力，同理好的教材亦然。顯然，阿草已開闢出一條獨特的清幽路徑。
筆者心目中理想的數學教育應展示整個求知的探尋過程：從問題（problem）出發，作知識與思考的總動員，之後得到發現（discovery）或猜測（conjecture），接著是作檢驗（test），即證明（proof）或否證（refutation），最後得到無上妙趣的了悟（understanding）。在進行這個過程時，順便將問題的情況與背景溶入，這包括文化的、歷史的資料，數學家的生平、趣事與美妙的想法等等。我們除了要知道一個定理的證明之外，更重要的是，還要知道定理是如何發現或看出來的。前者是「邏輯上的為什麼」（logically why），後者是「心理上的為什麼」（psychologically why），兩者都要兼顧，不可或缺。
科學哲學家馬赫（E. Mach,1838-1916）說：「你無法了解一個理論，除非你知道它是如何發現的。（You can not understand a theory unless you know how it was discovered.）」對於數學的學習，發現與證明兼備才算完全。
如何達到上述的理想呢？
讓我們考察一下文獻。正規的數學書或文章，絕大多數都只展示邏輯演繹系統，定義定理證明，「亡象而存玄珠」，抽象冰冷得「不食人間煙火」。轉到數學史中去追尋，又只看見到處是史實的堆積，而流於「斷爛朝報」的「集郵式」知識，還是無法解求知之渴。忽聞科學哲學（philosophy of science）是講究科學知識的生長、演化與科學方法論的學問，但是進到裡面，不免又讓人失望了，因為儘是「天馬行空」的迷茫。
似這種落空與失望的感覺，我們在禪宗的歷史中也找到一個例子。禪宗第二代祖師慧可（487-593，達摩是初祖），他在博覽群書之後，每嘆曰：
孔老之教，禮數風規；說得真是淋漓盡致，所以他改追隨達摩學禪。
莊易之書，未盡妙理。
回到數學教育來，我們應該連結正規數學、數學史與科學哲學，三者合而冶之，這樣或許可以找到比較滿意的解決之道。 哲學家康德（I. Kant, 1724-1804）說：
哲學缺少科學是空的，科學缺少哲學是盲的。科學哲學家I. Lakatos（1922-1974）把它修改為：
科學哲學缺少科學史是空的，科學史缺少科學哲學是盲的。那麼，優秀的數學教育（或數學通識教育）應以數學內容為主軸（不能打折或避重就輕）， 揉合（或整合）數學史、科學史與科學哲學，來合理地重建（rational reconstruction）數學知識的發現、 試驗與證明的生長過程，參見圖一。
圖一：優秀的數學教育應以數學內容為主軸，揉合數學史、科學史與數學哲學，來合理地重建數學知識的發現、試驗與證明的生長過程。 |
再打個比方來說，我們要儘可能地考察數學發展的全貌：從種子落地、發芽、生長，到開花結果， 這是內在生命機理。另外，我們也要顧及外在的風、雨、陽光與氣候變遷，以便「參贊化育」， 最終是期望達到教育的至高目標：「Teach to think」，點燃學生思想火炬。
如果我們採用上述高標準的觀點，來檢驗《阿草的葫蘆》，我們可以肯定地說：阿草寫得相當成功， 並且已到達爐火純青的境界。筆者在讀得趣味盎然之餘，不忍獨享，於是情不自禁要將它介紹給年輕學子、 中學數學教師以及廣大社會業餘的數學愛好者。對於有心想要進入數學世界，了解數學，品味數學的人， 這是一本絕佳的入門書。對於那些先前被「不當的數學」嚇壞或教怕而得到「數學恐懼症」的人， 筆者更要建議，不妨拿起阿草這本書來讀，給自己一個機會，也許可以重新跟數學和解，開始喜歡數學。 欣賞數學之美跟欣賞精緻藝術的眼光與功力差不多，雖不易建立，但值得培養。 阿草在書中隨時都埋下了數學美感經驗的種子，這是目前數學教育最欠缺的一環。
現在讓我們來考察全書的內容，由表入裡。
首先，一打開書，就覺得清爽悅目，插圖生動精美，有的甚至遠赴國外實地拍攝。更特別的是，版面上的留白很大，也許阿草有意要避免費瑪（Fermat）事件的重演。每一章下方都附有一句小格言，很適切地表達阿草對數學或該章的心得結晶。接著，主文的取材有趣，行文流麗，具有特殊的「阿草風味」，即簡潔中又含智性幽默。
其次，我們觀看內涵。全書一共有十四章，各章基本上是獨立的，並且形成一個圓足的小世界。這樣的好處是，讀者可以從任何一章切入，而不必擔心前後不連貫的問題。從數學的各分支來看，我們可以將全書的內容分類如下：
- 數學家的故事：這是第一章的內容，講述阿基米得（Archimedes, B.C. 287-212）、
柏努力（Jakob Bernoulli, 1654-1705, Jakob I, Jacques I 或James皆指同一人）、
高斯（Carl Friedrich Gauss, 1777-1855）等四人的得意傑作及其墓碑上所刻的幾何圖形，
由此展開許多有趣數學之討論。值得順便一提的是，物理學家波茨曼（Ludwig Boltzmann，1844-1902）的墓碑上刻的是他的著名公式：
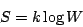
其中S表熵（entropy），k為波茨曼常數，W表熱力系統在給定宏觀狀態下所包含的微觀狀態數。 再作一對照：物理定律的數目偏好3，例如克卜勒三定律、牛頓三運動定律、熱力學三定律； 而數學公理偏好5，例如歐氏幾何的五公理，皮亞諾（Peano）自然數的五公理。 - 天文曆算：這是第三章的內容。從科學史的眼光來看，天文學是數學與物理學的故鄉， 是數學問題與數學發現的豐富泉源。燦爛的星空，行星的運行，季節的變換，除了讓人感受到大自然的規律， 更激起人們無窮的想像力與敬畏之情，於是展開無止境的求知探尋活動。阿草安排這一章，有他的偏好， 也有他的遠見。
- 幾何學與三角學：這是第二、五、六、七、八章的內容，包括有平面的、立體的與球面的情形。 這部分從取材、觀點、趣味、思考方法，到美的欣賞，都有阿草獨到的領略， 可以補足目前平淡無趣的高中數學。
- 微積分：這是第四、九章的內容。大自然利用微積分在大地上行事，但是要掌握微積分卻不容易， 微積分變成大一新生最感頭痛的一門課。阿草在第九章短短的三十五頁中， 就將微積分兩千餘年的發展之來龍去脈簡潔地說清楚。因此，筆者建議年輕學子，若第一次要唸微積分， 不妨由第九章切入，精讀，保證可以讓你愉快地、直指本心地進入微積分的堂奧。 對於人生的「第一次」要非常慎重與珍惜。
- 科學方法論：這是第十、十二、十四章的內容。
科學方法包括統計方法與數學的各種猜測式推理（plausible reasoning）。
後者例如，歸納法、分析與綜合法、類推法、試誤法、推廣、特殊化（或極端化）、
量綱檢驗、對稱性觀察、局部推理、大膽假設、小心求證、想像力、
等等。前者大致又分成三個層次：
一、蒐集資料，二、整理、比較與分析資料，三、拋出假說，推出結論，
解釋既知且預測未知。阿草選取黑龍（Heron）公式（其實是阿基米得首創）、
哥倫布發現美洲大陸、達爾文創立演化論，孟德爾探索遺傳定律等著名例子，
來說明科學方法的運用。這些都是數學史、科學史與科學哲學研究的絕佳題材。
筆者特別喜歡第十二章，關於黑龍公式的探索過程，從發現與證明，
到欣賞與方法論都齊備，講得實在太精彩了。
- 混沌與碎形：這是第十一章的內容，是近年來新興的一門學問，跟電腦的關係密切。 為了趕上時代，阿草好學不倦，投入時間研讀，再利用通俗的話語介紹給讀者。
- 數學教育與解題：這是第十二、十三、十四章的內容。
解題訓練是數學教育的核心工作。哲學家叔本華說：
當一個人被某個問題所困，問題逐漸占據整個身心，如果他能夠找到一條解決的出路， 那麼他就成為一個哲學家。
此地叔本華所說的問題是指哲學上的大問題。 事實上，我們把「問題」改為「數學問題」，「哲學家」改為「數學家」， 也行得通。準此以觀，數學教育最要緊的是讓學生得到獨立的解題經驗， 從中鍛鍊思想力與毅力。阿草舉了許多例子，實地作解題的「講道說法」， 讀者可先模仿，然後再找出最適合自己的一條道路。 只有當一個人嚐過獨立解題的樂趣後，他才會喜歡數學，並且終身難忘， 導致持久的追尋。
- 「Dimension」的翻譯問題本書大量使用「因次」與「單位因次」之名稱，
這是從「Dimension」翻譯過來的，筆者認為值得商榷。
「Dimension」在幾何學、線性代數、拓樸空間與碎形中都出現，通常是指空間的維數」， 例如我們說三維空間或 n 維向量空間。古老一點的譯法，叫做三度空間或 n 度向量空間， 現在已不通行了，但偶而還可以看得到。另外，日本人將「Dimension」譯為「因次」，也有人加以引用， 例如三因次空間。顯然，「維」比「因次」好，而「度」容易跟「溫度」與「角度」的「度」混淆。
其次在物理學中，探討物理量的單位時也用「Dimension」這個字，例如速度的「Dimension」為LT-1， 其中L代表長度，T代表時間。此時「Dimension」譯為「量綱」較適切， 最好不要譯成「維」或「因次」或「單位因次」。 日本人並不加以分辨，只要見到「Dimension」，一律譯為「因次」，不管它是在數學或物理學中出現。
進一步，在物理學中有一個方法叫做「Dimensional Analysis」， 這是利用各物理量之間的「量綱」（dimension）關係，來檢驗一個公式或猜測出一個公式。 此時千萬不可以將「Dimensional Analysis」譯成「維的分析」或「因次分析」（在台灣筆者曾見過這兩種譯法）， 而應該譯為「量綱分析」。
- 頁11，費瑪最後定理，在1995年已由威列斯（Wiles）證明，但書上卻說「還未確定完全成功」。
- 頁16補上阿基米得墓碑上的幾何圖形。
- 頁17補上史帝文（Stevin）墓碑上的說明文字："Wonder en is gheen wonder" （The Marvel is No Marvel或The Miracle is NoMiracle）。
- 頁19說柏努力墓碑上的三個拉丁字沒刻上去，其實是刻上去了，只是螺線刻錯而已。另外，本頁的等角螺線，圖畫得不正確。
- 頁37第四個圖，標示為「無名氏的證法」，事實上這是達文西（Leonardo da Vinci）的證法。
- 頁45的圖，再補上另一半赤道虛線，則較正確而且有立體感。
- 本書對於伽利略Galileo（名）Galilei（姓），皆按慣例用姓氏Galilei稱呼， 但是我們發現幾乎所有的外文書都採用Galileo。據筆者查究的結果，伽利略是以名字稱呼通行的。 另一位是拿破崙（Napolean）。
- 頁63補上克卜勒第三定律，因為本書後來經常引用。
- 頁78中間說：「人口增長呈幾何級數」，而前幾頁都說：「人口增長呈幾何數列」。
馬爾薩斯（Malthus）在1798年的「人口論」裡說，人口的增長呈「Geometric progression」，
糧食的增長呈「Arithmetic progression」，其中progression有譯成「級數」，也有譯成「數列」，
在從前馬馬虎虎。但是，今日級數是指series，數列是指sequence，意義不同，應當要嚴格區分。
- 頁85有關e的級數表示法應稍加修正。
- 頁86的圖，左端的地方不正確。同頁下方，常態分布鐘形曲線應改為
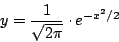
- 頁145，蜂巢的「頂面」應為三個全等的菱形，而不是三個全等平行四邊形。 同頁阿基米得球體體積求法之圖，應可作得更好一點。
- 頁308說，到目前為止還找不到第n個質數的公式。事實上，在1964年Willans就已經找到了。
最後，我們希望阿草不斷地「寫、寫、再寫」，寫出更多的佳作，我們拭目以待。
後記：筆者曾參與阿草在台大數學系主持的「高中數學學習成就優異學生的輔導實驗計畫」，大約有十年之久， 這是筆者跟通識教育結緣的契機。去年筆者在台大開授「微積分與西方文明」的通識課，原打算寫一教本， 但發現工程浩大，又無阿草的勤快，故不知何年才能完成。據筆者所知， 中央大學王九逵教授也寫有《邏輯與數學思維》的通識教本（新竹凡異出版社，83年9月初版）， 相當有特色與精闢的見地。
