首頁 | 搜尋

．原載於科學月刊第二十九卷第十二期
．作者當時任教於台大數學系
 

猴子敲打出莎士比亞全集

蔡聰明

 
 

莎士比亞全集是人類天才智慧的至高創造，然而今人驚奇的是機率論可以證明： 一隻猴子在打字機前任意地且不斷地敲打下去，殆確（almost sure，即機率為 1） 可以得到莎士比亞全集。下面我們就來介紹這個奇妙的結果。

首先將莎士比亞全集翻譯成摩斯電碼（Morse code，例如 ‥·––– ‥·表示 SOS），得到由點與線段所組成的一長串符號，長度雖然很長，但終歸是有限。

其次，猴子的打字也翻譯成摩斯電碼：敲打出一個點或一個線段的機率各為$\frac{1}{2}$。猴子不斷地敲打下去就可以得到一個無窮序列之摩斯電碼。

接著我們考慮一個銅板，其有正面 (head) H 或反面 (tail) T。 將此銅板獨立地且不斷地丟下去，就得到一個銅板序列（又叫做樣本點）

\begin{displaymath} \omega =(\omega_1 , \omega_2 ,\cdots ,\omega_n,\cdots) \end{displaymath}

所有可能的銅板序列全體就組成樣本空間 (Sample space)：

\begin{displaymath} \Omega ={\omega=(\omega_1 , \omega_2 ,\cdots ,\omega_n,\cdot... ...ily{cwM1}\fontseries{m}\selectfont \char 67}} T,n \in \bf {N}} \end{displaymath}

現在將 H 與 T 分別對應線「－」與點「．」，於是一個銅板序列就對應一個摩斯電碼序列，反之亦然。從而猴子打字就相當於丟一個公正銅板 (a fail coin)。因此，我們的問題就轉化成：不止息地丟一個公正銅板，可以得到莎士比亞全集的機率是多少？

機率論所要研究的對象是涉及說不準 (uncertainty) 的隨機現象。在思考上，我們必須分辨現實 (realization) 與可能 (possibilities)。作個隨機實驗，得到一個現實 ω（又叫樣本點），相應就有所有可能結果所形成的樣本空間 Ω，現實 ω 只是樣本空間 Ω 的一個元素。機率論就是要相對於一個樣本空間 Ω，衡量其中一個事件 (event) $A \subset \Omega$ 的機率大小。這必須對一個隨機實驗建立機率空間 $(\Omega,F,P)$，其中 F 為事件全體，P 為一個機率測度。在這個架構之下，對 A $\in$ F 求算機率 P(A)。

對於「無窮多次丟銅板」這個複雜的隨機實驗，根據測度論 (measure theory)，我們可以適當地為其建立一個機率空間 ($\Omega,F,P$)。我們要問：一串符號模式 (pattern)，例如「HTTH」或「莎士比亞全集」，在銅板序列中發生的機率是多少？

首先我們考慮「H」模式的特例。不斷地丟一個公正銅板，直觀經驗告訴我們，幾乎可以確定 H 會不時地出現。

為了闡明這個直觀結果，我們先作一般的準備。設 $(A_n) \subset F$ 為一列事件，令它們不時地發生之事件為 B，那麼 B 的結構是什麼呢？

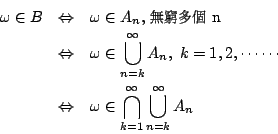
\begin{eqnarray*} \omega \in B &\Leftrightarrow & \omega \in A_n \mbox{, {\fontf... ...w & \omega \in \bigcap_{k=1}^{\infty} \bigcup_{n=k}^{\infty} A_n \end{eqnarray*}


所以

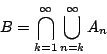
\begin{displaymath} B=\bigcap_{k=1}^{\infty} \bigcup_{n=k}^{\infty} A_n \end{displaymath}

通常我們簡記， $\bigcap_{k=1}^{\infty} \bigcup_{n=k}^{\infty} A_n$ 為 (An, i.o.) 這表示 An 不時地發生的事件，i.o.是“infinitely often”之縮寫。

另一方面，事件 $\bigcap_{k=1}^{\infty} \bigcup_{n=k}^{\infty} A_n$ 代表什麼意思呢？

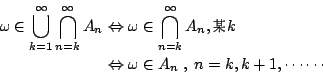
\begin{eqnarray*} \omega \in \bigcap_{k=1}^{\infty}\bigcup_{n=k}^{\infty} A_n &\... ...\\ &\Leftrightarrow&\omega \in A_n \; , \; n=k,k+1,\cdots \cdots \end{eqnarray*}


因此， $\omega \in \bigcap_{k=1}^{\infty} \bigcup_{n=k}^{\infty} A_n $ 表示，除了有限多個指標之外，對其餘的指標 n 皆有 $\omega \in A_n$ (for all but finitely many n)。換言之， $\bigcap_{k=1}^{\infty} \bigcup_{n=k}^{\infty} A_n$ 表示 An 終究 (eventually) 要發生的事件。

由集合運算的 De Morgan 法則知道

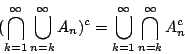
\begin{displaymath} (\bigcap_{k=1}^{\infty}\bigcup_{n=k}^{\infty} A_n)^c= \bigcup_{k=1}^{\infty}\bigcap_{n=k}^{\infty} A_n^c \end{displaymath}

並且顯然有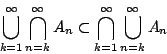

\begin{displaymath} \bigcup_{k=1}^{\infty}\bigcap_{n=k}^{\infty} A_n \subset \bigcap_{k=1}^{\infty}\bigcup_{n=k}^{\infty} A_n \end{displaymath}

模仿數列的上極限 (upper limit) 與下極限 (lower limit) 的定義，我們也有如下的極限概念。

定義：
當 $\bigcap_{k=1}^{\infty}\bigcup_{n=k}^{\infty} A_n = \bigcup_{k=1}^{\infty}\bigcap_{n=k}^{\infty} A_n =A$ 時， 這個共同集合 A，叫做 (An) 的極限，記為 $\lim_{n \rightarrow \infty } A_n =A$
由機率的演算規則，我們可以證得下面兩個定理。

定理1：(機率測度P的連續性)
若 $\lim_{n \rightarrow \infty } A_n =A$， 則 $\lim_{n \rightarrow \infty}P(A_n) =P(A)$、

定理2：
(i)Boole不等式：

\begin{displaymath} P(\bigcup_{K=1}^{n}A_k)\leq \sum_{k=1}^{n} P(A_k) \end{displaymath}

(ii)次可列加性(countable subadditivity)：

\begin{displaymath} P(\bigcup_{K=1}^{\infty}A_k)\leq \sum_{k=1}^{\infty} P(A_k) \end{displaymath}

事件 (An i.o.) 的機率是多少？ 由定理1與定理2知

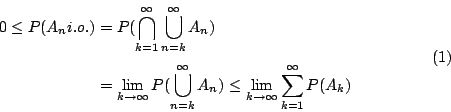
\begin{displaymath} \begin{eqalign} 0 \leq P(A_n i.o.) &= P(\bigcap_{k=1}^{\inft... ...row \infty} \sum_{k=1}^{\infty} P(A_k) \end{eqalign}\eqno{(1)} \end{displaymath}

所以，如果 $\sum_{k=k}^{\infty} P(A_k) < \infty$（收斂）， 則 $\lim_{k \rightarrow \infty} \sum_{n=k}^{\infty} P(A_n)=0$， 於是

\begin{displaymath} P(A_n i.o.)=0 \eqno{(2)} \end{displaymath}

但是，如果 $\sum_{k=1}^{\infty} P(A_k) = + \infty$（發散）， 由(1)式我們對於 P(An i.o.) 得不到什麼結論。然而。若再加上 (An) 為一列獨立事件，那麼由不等式

\begin{displaymath} 1-x \leq e^{-x} \quad \forall x \in \mathbf{R} \end{displaymath}

就得到

\begin{displaymath} P(A_n)^c=l-P(A_n)\leq e^{-P(A_n)} \end{displaymath}

從而

\begin{eqnarray*} 0 &\leq & P((\bigcup_{n=k}^{\infty}) A_n)^c) = P(\bigcap_{n=k}... ...od_{n=k}^{m} e^{-P(A_n)}\\ &=& e^{-\sum_{n=k}^{\infty} P(A_n)} \end{eqnarray*}


當 $m \rightarrow \infty$，上式最後一項趨近於 0，因此，對任意 $k = 1,2, \cdots$， 恆有 $P(\bigcap_{n=k}^{\infty} A_n^c)=0$，於是

\begin{displaymath} P[(\bigcap_{k=1}^{\infty} \bigcup_{n=k}^{\infty}) A_n)^c] =P... ...=\lim_{k \rightarrow \infty} P(\bigcap_{n=k}^{\infty} A_n^c)=0 \end{displaymath}

由此可得

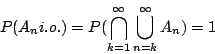
\begin{displaymath} P(A_n i.o.) = P(\bigcap_{k=1}^{\infty} \bigcup_{n=k}^{\infty}A_n) = 1 \end{displaymath}

定理3 （Borel-Cantelli 補題）
假設 (An) 為機率空間 $(\Omega,F,P)$ 中的一列事件，那麼我們有

(i) 若 $\sum_{n=1}^{\infty} P(A_n)<\infty$，則 P(An i.o.)=0

(ii) 若 $\sum_{n=1}^{\infty} P(A_n) = + \infty$ 且 (An) 是獨立的，則 P(An,i.o.)=1

註：(i)與(ii)分別叫做第一與第二 Borel-Cantelli 補題。

定理4 （Borel 0-1 律或 Borel 兩條路定理）
假設 (An) 為機率空間 $(\Omega,F,P)$ 中的一列獨立事件，那麼 P(An i.o.)=0 或 1，端視 $\Sigma_{n=1}^{\infty} P(A_n)$ 為收斂或發散。

現在回到先前的問題：在銅板序列中，模式「H」不時地出現之機率是多少？令 Hn 表示第 n 次丟銅板，出現正 (H) 之事件，那麼 (Hn) 是獨立的，並且 $P(H_n) = \frac{1}{2}$。於是

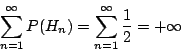
\begin{displaymath} \sum_{n=1}^{\infty} P(H_n)= \sum_{n=1}^{\infty} \frac{1}{2} = + \infty \end{displaymath}

由定理3的(ii)知，P(Hn i.o.)=1，即不時地出現正面的機率為 1。

進一步我們問；有限模式「HTTH」不時地出現之機率是多少？

今 En 表示「HTTH」的模式在丟第 n 次銅板時開始出現之事件，亦即

\begin{displaymath} E_n = H_n \cap H_{n+1}^c \cap H_{n+2}^{c} \cap H_{n+3} \end{displaymath}

於是

\begin{displaymath} P(E_n)=(\frac{1}{2})^4=\frac{1}{16} \end{displaymath}

從而 $\sum_{n=1}^{\infty} P(E_n)= +\infty$，不巧的是，(En) 不互相獨立，所以我們不能使用第二 Borel-Cantelli補題。還好，事件 $E_1, E_5, E_9, \cdots \cdots E_{4k+1} \cdots \cdots$ 是獨立的， 並且 $\sum_{k=1}^{\infty} P(E_{4k+1}) = + \infty$，故由第二 Borel-Cantelli 補題知 P(E4k+1 ,i.o.) = 1，今因 $(E_{4k+1} i.o.) \subset (E_n i.o.)$，所以

\begin{displaymath} 1=P( E_{4k+1} i.o.) \leq P(E_n i.o.) \leq 1 \end{displaymath}

立即得到

P(En i.o.)=1

換言之，模式「HTTH」不時地出現之機率是 1。

同理可證，任何由 H 與 T 所組成的有限長度之模式，在銅板序列中不時地出現之機率也是 1。因此，我們就證明了下面的驚人結論：

定理3：
猴子不時地敲打出莎士比亞全集的機率為 1。

豈止是敲打出而已，是不時地敲打出且機率為 1，這個結果跟直觀常識似乎是矛盾的，故被稱之為 Borel 詭論 (Borel paradox)。什麼是天才的創造？機運或偶然？堅持或努力？

從另一個角度來看，這也反映出如果生命「無窮」並且「永不止息」地工作下去， 會產生石破天驚的成果，沒有什麼事是辦不到的。愚公移山是另一個例子。

莊子說：「吾生也有涯，而知也無涯。以有涯逐無涯，殆矣！」然而，數學或人間許多浪漫情事，恰好就是「以有涯逐無涯」所完成的。

 
對外搜尋關鍵字：
．測度論

回頁首
 
（若有指正、疑問……，可以在此 留言 或 寫信 給我們。）
EpisteMath

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有


編輯：朱安強 最後修改日期：2/17/2002