.原載於科學月刊二十五卷十一期
.作者當時任教於台大數學系
蔡聰明
|
|
.原載於科學月刊二十五卷十一期 .作者當時任教於台大數學系 | ||
|
談分析與綜合法
蔡聰明 |
|
如果我們相信任何複雜的事物或事理都是由一些基本的要素組成的, 則自然就衍生出分析與綜合的研究方法。先利用分析方法找出基本要素, 然後再用綜合方法由基本要素去組合成複雜的事物。 從而達到對事物或事理的結構之澄清與了解, 並且引伸出「以簡馭繁」的要領。本文我們試圖闡明分析與 綜合法在數學與科學中所扮演的角色。 作為一個重要的科學方法,分析與綜合法 (the Method of Analysis and Synthesis)在數學的發展史上,扮演著主導的角色。 幾乎每一個數學分支都有它的蹤跡,有的甚至還以它來命名, 例如綜合幾何、解析幾何、分析學、調和分析等等。 本文我們要闡明分析與綜合法的各種意思, 以及它跟各支數學發展的關連。例如,微積分及其後續發展為何叫做分析學?
對於事物與事理的剖析,分別產生了「本義的」與「引伸的」分析與綜合法這兩層意思。
|
對外搜尋關鍵字: .不可共度 .畢氏學派 .利瑪竇 .徐光啟 .Vieta .Wallis .Descartes .Fermat .the method of exhaustion .牛頓 .微積分根本定理 .Taylor .Fourier .刻卜勒 .Euclid |
對於「事理」的結構如何剖析呢?一個敘述 (statement) 或命題 (proposition) 如何找到支持的理由? 在數學中,一個公式、定理或猜測總是以命題「若 p 則 q」的形式來出現, 其中 p 叫做前提或假設,q 叫做結論。如何證明或否證一個命題呢? 所謂「證明」就是要找出從 p 連結到 q 的一條邏輯通路,這有時可真不容易, 因為「真理往往藏得很深」。古希臘人想出一種「倒行逆施」的辦法: 由結論q切入,即假設q成立,投石問路一番, 看看能夠引出什麼結果,這就是所謂的分析法;等到抓得要緊的理由後, 再回過頭來作演繹式的綜合,完成證明。 分析與綜合有各種的「主題變奏」(variation of the theme):
接著是作綜合:取 M 為 BC 之中點,過 A 點作一直線平行於 PM 且交 BC 於 Q 點,連結 PQ 即為所求。
換句話說,所謂分析法就是由一個敘述或猜測 A 出發,假設它成立,
然後推導出一系列的結果:
如果 K 是錯誤的或矛盾的,那麼立即就否定掉A,這叫做歸謬證法。 如果己知K是成立的,那麼K就是A的一個必要條件,此時A可能成立也 可能不成立;如果(4)式的每一步皆可逆,那麼 我們由K就證明了A,這叫做綜合。此時K又是A的充分條件,於是A與K互為充要條件。 亞里斯多德已經指出來,由錯誤的前提可以推導出荒謬的結論,也可以推導出正確的結論。
例如,英國著名數學家羅素 (B. Russell) 有一次在宴會上,大家給他出一個難題,要他證明 Russell=Pope(當時的教宗)羅素立即證明如下:
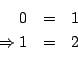
因為 Russell 與 Pope 是2個人,所以 Russell 與 Pope 是1個人。 這跟希柏特 (Hilbert) 的名言:「如果 0=1,則女巫從煙囪飛出來」,異曲同工。
當我們斷言:「若p則q」(
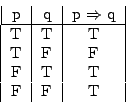
因此,「如果 0=1,則三角形三內角和為 180°」,這是對的。 另外,在正確的推理之下,前提的真必可保證結論亦真。 總結上述,由結論或所發生的結果或所觀測到的現象,要探求其原因, 通常就用分析法;反過來,由原因推導出結果,完成證明或求得解釋, 就是綜合法。德謨克利特斯說:「我寧可要尋得一個原因, 而不要得到波斯帝國。」(I would rather discover one cause than gain the kingdom of Persia.) 一般而言,綜合較單純且平凡,分析較複雜且多變。在算術中已有許 多例子,例如已知雞有17隻,兔有13隻,則雞兔總共有30隻,腳有86叟, 這可以看作是平凡的綜合;反過來,已知雞兔一共有30隻,腳共有86隻, 要問雞兔各有幾隻,這就是小學生最感困難的雞兔同籠問題, 是展現分析法的好題目,最好的解題辦法是代數方法。另外, 算術根本定理更是分析與綜合法的產物。
|
|
|
|
|
(若有指正、疑問……,可以在此 留言 或 寫信 給我們。) |
|
|
|
EpisteMath (c) 2000 中央研究院數學所、台大數學系 各網頁文章內容之著作權為原著作人所有 |
| 編輯:洪瑛 / 繪圖:簡立欣 | 最後修改日期:2/17/2002 |