.原載於科學月刊第十七卷第五期
.作者當時任教於台大數學系
•註釋
曹亮吉
|
.原載於科學月刊第十七卷第五期 .作者當時任教於台大數學系 •註釋 | |||
|
以簡馭繁
曹亮吉 |
|
在數學的發展過程中,以簡馭繁的精神到處可見。在所有的計算中,加減最簡單, 乘除次之,開方又更難。於是發明了對數,把乘除歸於加減 註1 。又發明各種只用及四則運算的辦法,來處理開方的問題 註2。 在微積分中,這種以簡馭繁的精神,無論是在觀念方面或是在計算方面,更是俯拾皆是。
有了一個函數 f(x),我們考慮平均變化量
積分的觀念始於求面積。假設我們要求曲線 y=f(x) 之下,x 軸之上,兩縱線 x=a 及 x=b 之間的面積 A,如圖一。
將線段 [a,b] 分割成 n 小段 [xk-1,xk],
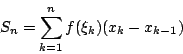
可以當做 A 的一個近似值。而當 n 趨向無窮大,每小段 [xk-1, xk] 之長趨近於 0 時,此近似值就變成 A 的正確值。此值稱為函數 f(x) 在 [a,b] 之間的積分,記做
如果 x 代表時間,f(x) 代表速度,則
這種分割、取點、求和、求極限的四部曲,不但可用來算面積,求距離,只要變數與函數解釋得當,也可用來求曲線長、體積、質量、質量重心、功等等 。積分這個簡單的觀念一樣統攝了許許多多的現象。 微分與積分的觀念雖然簡單,但牽涉到的計算卻是極限這種無窮的步驟,與四則運算的有限性相較是難了太多。於是以簡馭繁的辦法又一再出現了。
我們發現微分的運算與函數的四則及合成運算之間有些簡單的關係:
![\begin{eqnarray*}
(f\pm g)'(x_0) &=& f'(x_0)\pm g'(x_0) \\
(f\cdot g)'(x_0) &=&...
...] / g(x_0)^2 \\
(f\circ g)'(x_0) &=& f'[ g(x_0) ] g'(x_0)
\end{eqnarray*}](img9.gif)
有了這些關係式,我們只要知道簡單函數的微分,就能算得複雜函數的微分。譬如知道了單項式 xn 的微分,就知道分式的微分;知道了正、餘弦函數的微分,就知道任何複雜的三角函數的微分等等,而且這些計算都是在有限步驟中就可以完成的。 積分也類似,相當於微分的加減公式,積分也有加減公式,相當於微分的乘法公式,積分有分部積分的公式,相當於微分的合成公式,積分有變數代換的公式。可惜相當於微分的除法公式,積分並無適當的公式,所以一般說來,積分的計算要比微分的難得多。不過關於除法,積分並不是一籌莫展的。譬如我們可以用部分分式的辦法,把一複雜的分式,表成簡單分式之和,而這些簡單分式的積分幸而都有辦法計算得到。這也是一種以簡馭繁的方法。 微積分的另一大功能在於計算函數的值。分式是由變數的四則運算所組成,所以其函數值在有限步驟內都可以計算出來。其他函數則不然,譬如三角函數、對數、指數、開方等,除了一些特別值外,都不可能用有限的步驟計算得到。為此,微積分中的 Taylor 公式提供了在有限步驟就能求得近似值的辦法,又能估計此近似值與真值之間的誤差。
Taylor 公式說,一個函數 f(x) 可以寫成為兩部分
f(x)=Pn(x)+Rn(x)
Pn(x) 為一多項式 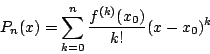
可由 f(x) 在有限步驟內算得。
Rn(x) 稱為餘式;我們希望
如此一來,f(x) 就等於其 Taylor 級數 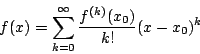
而 Pn(x) 可做為 f(x) 的近似值,Rn(x) 可用來估計誤差。
Rn(x)的表示方法有多種,最常見的為下面的積分型及微分型兩種:
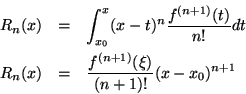
以 f(x)=ex, x0=0, x>0 為例,則因 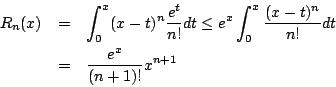
或 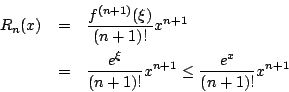
而 譬如取 n=10, x=1,則 e 以 為其近似值,而其誤差 簡言之,我們以簡單的四則運算求得 e 的一個近似值,同時也由簡單的計算估計得此近似值的誤差。三角函數值、對數值、指數值、開方值等等無不用此方法,求得近似值及估算其誤差。以簡馭繁的精神,在 Taylor 公式中表露無遺。
n=0 時,積分型餘式的 Taylor 公式就變成
它正是微積分基本定理。而積分型餘式的 Taylor 公式正是由此基本定理,經一再分部積分得到的。
n=0 時,微分型餘式的 Taylor 公式就變成
它正是平均變率定理。平均變率定理的擴張為 Cauchy 定理 將 Cauchy 定理一再用到 就可求得微分型餘式的 Taylor 公式。 Taylor 公式不但提供了計算及估計的方法,而且隱含了微積分最基本的兩個定理:微積分基本定理及平均變率定理。掌握了 Taylor 公式,就是以簡馭繁地掌握了大半的微積分學。
|
對外搜尋關鍵字: .微分 .積分 .極限 .分部積分 .變數代換 .Taylor公式 .微積分基本定理 .平均變率定理 .Cauchy定理 |
|
|
|
|
(若有指正、疑問……,可以在此 留言 或 寫信 給我們。) |
|
|
|
EpisteMath (c) 2000 中央研究院數學所、台大數學系 各網頁文章內容之著作權為原著作人所有 |
| 編輯:石莉君 / 校對:康明軒 / 繪圖:簡立欣 | 最後修改日期:2/17/2002 |