怎麼說它有多彎？

．原載於科學月刊第十六卷第八期
．作者當時任教於台大數學系

怎麼說它有多彎？

曹亮吉

曲線與曲面的特性在其彎曲。在數學上，我們不似要說它們是彎曲的，而且還得說它們彎曲到什麼程度。衡量彎曲的程度，在數學上叫做曲率。我們先談小面曲線的曲率。

先說直線，它到處都平直不彎曲，所以曲率到處都是 0。再看圓，一個圓的彎曲程度到處都一樣，所以曲率是個常數；但大的圓比小的圓平直些，所以大的圓的曲率要較小的來得小。若大小兩圓的半徑各為 R 及 r，則同樣繞了一圈(彎曲了一圈)，大圓要花 $2\pi R$ 的弧長，而小圓則為 $2\pi r$ ，所以 $\frac{1}{R}$ 與 $\frac{1}{r}$ 應該可以描述大小兩圓的彎曲程度，也就是說圓的半徑的倒數，就是圓的曲率。

圖一

以上是就整個圓而討論的。就局部而言，圓的彎曲可以其切線斜角的變化來衡量。斜角的變化與弧長的變化之商代表曲度的平均變化率，如圖一，設圓 O 的半徑為 R，我們很容易看出來：從 P 點到 Q 點切線斜角的變化 θ 正好是 $\angle POQ$ ，而弧長的變化 $\widehat{PQ}$ 正好是 $R\theta$ ，兩者之商

$\begin{displaymath}\frac{\theta}{\widehat{PQ}}=\frac{\theta}{R\theta}=\frac{1}{R}\end{displaymath}$

所以圓的曲率恆為 $\frac{1}{R}$ 。

圖二

推廣到一般的曲線上，如圖二，我們可以考慮曲線從 P 點到 Q 點切線斜角的變化 θ, 將其除以弧長 $\widehat{PQ}$ ，然後讓 Q 點逼近 P 點，如此所得的極限值

$\begin{displaymath}K=lim_{P\rightarrow Q}\frac{\theta}{\widehat{PQ}}\end{displaymath}$

就稱為曲線在 P 點的曲率，顯而易見的是：由此定義求得的直線曲率為 0，而圓的曲率為其半徑的倒數。

從微分的觀點來看，曲線 y=f(x) 的曲率可看成切線斜角 $\theta=\tan^{-1}f'(x)$ 對弧長 $s=\int_{x_0}^x\sqrt{1+(f'(x))^2}dx$ 的變化率，含 f(x) 的一次及二次導函數。牛頓等人首先導出正確的公式：

$\begin{displaymath}K=\frac{f''(x)}{(1+f'(x)^2)^{\frac{3}{2}}}\end{displaymath}$

以拋物線 y=af(x)=ax² 為例，則因 f'(x)=2ax ,f''(x)=2a，所以曲率為 $\frac{2a}{(1+4a^2x^2)^{\frac{3}{2}}}$ 。當 x=0 時，亦即在拋物線的頂點處，曲率的值最大 (=2a)，而當 P 點離頂點愈遠，亦即 x 的絕對值愈大時，曲率愈小，這正符合我們對拋物線彎曲變化的印象。

圖三

我們可以把曲率做另一種幾何式的解釋：以 A 點為新坐標系統的原點，過 P 點的切線為新的 x 軸，則曲線的新的函數 y=f(x) 在 P 點，即 x=0 處的導函數為 0（因為切線就是 x 軸），所以曲率為 f''(0)。而此時 y=f(x) 的 Taylor 展式為

$\begin{displaymath}y=\frac{1}{2}f''(0)x^2+\cdots\end{displaymath}$

所以曲率

$\begin{displaymath}K=f''(0)=\lim_{x\rightarrow0}\frac{2y}{x^2}\end{displaymath}$

如圖三，y 代表 Q 點到切線的距離 QS, x 則為 PQ 在切線上的投影 PS，曲率變成

$\begin{displaymath}K=\lim_{Q\rightarrow P}\frac{2QS}{PS^2}\end{displaymath}$

這樣的幾何解釋和坐標系統無關。

如果用拋物線原來的公式 y=f(x)=ax²，P(x₀,y₀)，Q=(x₀,y₀)，則因切線方程式為 y-y₀=2ax₀(x-x₀)，由此可算得 QS,PS，經整理後得

$\begin{displaymath}\frac{2QS}{PS^2}=\frac{2a(1+(2ax_0)2)^{\frac{1}{2}}}{(1+2a^2x_0(x+x_0))^2}\end{displaymath}$

當 $Q\rightarrow P$ ，即 $x\rightarrow x_0$ 時，我們就得到拋物線原來的曲率公式。

有時候曲線的方程式以參數來表示比較方便： $x=x(\theta)$ , $y=y(\theta)$ ，這時候的曲率公式則為

$\begin{displaymath}K=\frac{y''x'-x''y'}{(x'^2+y'^2)^{\frac{3}{2}}}\end{displaymath}$

以橢圓 $x=a\cos\theta$ , $y=y(\theta)$ 為例，則

$\begin{displaymath}K=\frac{(-b\sin\theta)(-a\sin\theta)-(-a\cos\theta)(b\cos\the... ...}{2}}}=\frac{ab}{(a^2\sin^2\theta+b^2\cos^2\theta)^\frac{3}{2}}\end{displaymath}$

假定 a>b>0，則 $\theta=0$ ，π 時，曲率 $(=\frac{a}{b^2})$ 為最大，而當 $\theta=\frac{\pi}{2}$ ， $\frac{3}{2}\pi$ 時，曲率 $(=\frac{b}{a^2})$ 為最小，這和橢圓彎曲給我們的印象相符。（如果 a=b>0，則曲率永遠是 $\frac{1}{a}$ ，這正是半徑為 a 的圓。）再看雙曲線： $x=a\sec\theta$ ， $y=b\tan\theta$ ，此時

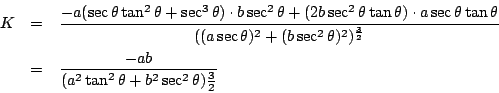
$\begin{eqnarray*} K&=&\frac{-a(\sec\theta\tan^2\theta+\sec^3\theta)\cdot b\sec^2... ...\\ &=&\frac{-ab}{(a^2\tan^2\theta+b^2\sec^2\theta)\frac{3}{2}} \end{eqnarray*}$

這裡的曲率之所以為負的原因是這樣的：弧長的方向以參數 θ 增加的方向為準，而順著這樣的方向，曲線一直在切線的右邊，所以切線的斜角（是 θ 的函數，但不是 θ 本身）一直在減少，其相對於弧長的變化率是為負值，因此曲率為負。如果 $y=a\sec\theta$ ， $y=-b\tan\theta$ ，則這組參數方程式仍然表示雙曲線，只是當參數增加時，曲線是左彎的(曲線在切線的左側，而根據曲率公式算得的曲率則為正數。我們的結論是這樣的；曲率的絕對值表示曲線彎曲的程度，曲率的正負則表示彎曲的方向（以參數為準）。回到原來雙曲線的曲率公式，我們發現在頂點時，即 $\theta=0$ ,π ，曲率的絕對值最大 $(=\frac{a}{b^2})$ 。而當曲線離開頂點越遠，即 $\vert\theta\vert$ 愈大，即曲率的絕對值愈小，而終於趨近於 0，這與雙曲線圖形給我們的印象相符。

以上所談的都是平面中的曲線。空間中的曲線除了彎曲外，還得看它扭離平面的程度，討論起來非常麻煩，我們就擱下不談。

在曲線上可以談曲率的先決條件是要有切線，而且切線的變化率也要存在；換句話說，曲線的函數要有二次以上的須函數。同樣的，要在曲面上討論曲率，我們要求它們的函數要有二次以上的偏導函數。過這樣的曲面上的任一點都有切平面；垂直於切平面而過切點的直線稱為法線。我們考慮一個含此法線的平面，它與曲面截成一曲線。我們可以以法線為軸，將此平面旋轉 φ 角 $(0\leq\varphi\leq2\pi)$ 就得到所有的含此法線的平面，這些平面與曲面相截所得一連串曲線所呈現的各個曲率 $K(\varphi)$ 全體，可做為曲面在該點的曲率。

也許直覺上我們會認為 $K(\varphi)$ 的變化可以非常大，它如何能有效地描述一曲面的彎曲程度呢？其實只要稍加說明，我們會發現 $K(\varphi)$ ， $0\leq\varphi\leq2\pi$ ，之間有沌地的關係。首先，我們知道在常態下（假設曲面有連續的二次偏導函數）， $K(\varphi)$ 為 φ 的連續函數。但 $K(0)=K(2\pi)$ ，所以所有的 $K(\varphi)$ 值組成實數上的一個閉區間 [K₂0xA141K₁]。也就是說 $K(\varphi)$ 有最大值 K₁，最小值 K₂，而其他的 $K(\varphi)$ 值都落在兩者之間，而且兩者之間的任何值都是某個 $K(\varphi)$ 值。不但這樣， Euler 還發現 $K(\varphi)$ 有如下的性質：若以 K₁ 的方向為 $\varphi=0$ ，即 $K(\varphi)=K_1$ ，則 $K(\frac{\pi}{2})=K_2$ ，亦即曲率最大及最小的兩個方向互相垂直。更有進者，在這種方向取法下， $K(\varphi)=K_1\cos^2\varphi+K\sin^2\varphi$ 。

要證明這個 Euler 的定理並不難。只要回到我們談過的曲線曲率的另一種幾何解釋就好：我們取所考慮的點為原點，該點的切平面為 x-y 面，則代表曲面的函數，其 Taylor 展式的常數項及一次項都要消失，所以

$\begin{displaymath} z=Ax^2+2Bxy+Cy^2+\mbox{ {\fontfamily{cwM2}\fontseries{m}\sel... ...us0.1pt{\fontfamily{cwM2}\fontseries{m}\selectfont \char 225}} \end{displaymath}$

更進一步，我們可以在切平面上選擇適當的 x 軸及 y 軸，使得 B=0（轉軸方法），因此

$\begin{displaymath} z=Ax^2+Cy^2+\mbox{ {\fontfamily{cwM2}\fontseries{m}\selectfo... ...us0.1pt{\fontfamily{cwM2}\fontseries{m}\selectfont \char 225}} \end{displaymath}$

設 $x=r\cos\varphi$ , $y=\sin\varphi$ 為含法線的平面，則相截的曲線為

$\begin{displaymath} z=r^2(A\cos^2\varphi+C\sin^2\varphi)+\mbox{{\fontfamily{cwM2... ...us0.1pt{\fontfamily{cwM2}\fontseries{m}\selectfont \char 225}} \end{displaymath}$

所以

$\begin{displaymath}K(\varphi)=\lim_{Q\rightarrow P}\frac{2QS}{PS^2}=\lim_{r\rightarrow O}\frac{2z}{r^2}\end{displaymath}$

若 $A\geq C$ ，則 A=K，為 $K(\varphi)$ 的最大值，而 C=K₂，為最小值。（若 A<C，則將 x,y 對調即可。）

我們來看一下幾個熟悉曲面的曲率。球的法線都過球心，含法線的平面截球面所成的曲線就是球面上的大圓孤，所以 $K(\varphi)$ 恆等於 $\frac{1}{R}$ -球半徑的倒數。

再看半徑為 1 的圓柱面。因為整個曲面總是在切平面的同一側，因此 $K(\varphi)$ 都是同號，可以假定都不小於 0。當含法線的平面與圓柱的軸平行時，它與圓柱面相截或一直線，所以此時 $K(\varphi)=0$ ，因此 $K(\varphi)$ 的最小值 K₂=0，而 $K_(\varphi)=K_1\cos^2\varphi$ 。K₁=K(0) 發生在與圓柱軸垂直的方向，此時的曲線是半徑為 R 的圓，因此 $K_1=\frac{1}{R}$ 。如此可得

$\begin{displaymath}K(\varphi)=\frac{1}{R}\cos^2\varphi\end{displaymath}$

事實上，當平面與軸成 $\frac{\pi}{2}-\varphi$ 角時，相截曲線為橢圓，其長軸為 $R\sec\varphi$ ，短軸為 R，切點正好是短軸的頂點，所以曲率為

$\begin{displaymath}\frac{R\sec\varphi\cdot R}{((R\sec\varphi)^2\sin^2\frac{\pi}{2}+R^2\cos^2\frac{\pi}{2})^{\frac{3}{2}}}=\frac{1}{R}\cos^2\varphi\end{displaymath}$

這和 Euler 的結果相符。

同理，圓錐面也有相同的曲率公式，只是 R 代表的是在切點，與軸相垂直所截圓的半徑。

再看雙曲拋物面

$\begin{displaymath}\frac{x^2}{a^2}-frac{y^2}{b^2}=cz\quad(c>0)\end{displaymath}$

的原點（馬鞍點），含法線的平面 $x=r\cos\varphi$ , $y=r\sin\varphi$ 與曲面相截成拋物線：

$\begin{displaymath}(\frac{\cos^2\varphi}{a^2}-\frac{\sin^2\varphi}{b^2})r^2=c^2z\end{displaymath}$

（ $\tan^2\varphi=\frac{b^2}{a^2}$ 時為直線），所以

$\begin{displaymath}K(\varphi)=\frac{2}{c}(\frac{1}{a^2}\cos^2\varphi-\frac{1}{b^2}\sin^2\varphi)\end{displaymath}$

我們發現

$\begin{displaymath}K_1=\frac{2}{ca^2}\quad,\quad K_2=-\frac{2}{cb^2}\end{displaymath}$

它們互為異號，這正表示切點附近的曲面同時會出現在切平面的兩側。

K₁,K₂ 稱為曲面在切點的主曲率，它們當然完全標示曲面在該處彎曲的程度。如果令 $H=\frac{1}{2}(K_1+K_2)$ , K=K₁K₂，則 H 與 K 當然也同樣標示曲面的彎曲程度，而且對某些問題而言，H 或 K 有時更具重要意義，而成為微分幾何探討的重要對象。（H 稱為均曲率，K 稱為高斯曲率。）

對外搜尋關鍵字：
．牛頓


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：李渭天 ∕ 繪圖：簡立欣

最後修改日期：2/17/2002