.原載於科學月刊第十四卷第一期
.作者當時任教於台大數學系
曹亮吉
|
.原載於科學月刊第十四卷第一期 .作者當時任教於台大數學系 | |||
|
實在而具體的數
曹亮吉 |
|
能滿足一整係數多項式方程式的數稱為代數數,否則稱為超越數。上回談實數觀念的歷史發展說,在十八世紀時有人猜測圓周率 π 是個超越數,可是終此世紀,數學家沒找出一個超越數來。 十九世紀初,Abel、Galois 等人證明:五次或五次以上的方程式的根,一般不能用方程式的係數經由四則運算及開方的方法來表示,所以一般代數數的模樣真是難以想像,更何況是超越數。1884年,Liouville 總算在超越數的研究方面有了大突破,他的主要定理如下:
用這個定理,Liouville 一下子就找出了一大堆超越數。
例中 x0 的無窮小數表示
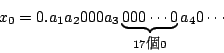
大部分位數為 0,而且連在一起的 0 的個數增加非常迅速,從證明中可以看出來,這正是 x0 為 超越數的原因。所以一般而言,如果一個無窮小數 中的指數 pm 迅速增加,超過一個程度(這個程度可用數學語言來表示),那麼它就是一個超越 數。 尋找個別超越數的故事當然不能不提下列兩件事:1874年 Hermite(1822∼1901年)證明 e 為超越數;1882年 Lindemann(1852∼1939年)證明 π 為超越數──證實了前此的猜測,也結束了化圓為方的美夢。
1900年,Hilbert(1862∼1943年)在第二次國際數學會上提出了二十世紀待解的23個數學大問題。其中第七個問題就是要證明 以上是對代數數、超越數個別認識的歷史,現在回過頭來看實數全體。 微積分有兩面,一面是應用,一面是本身的邏輯建構。由於深受希臘數學嚴謹的影響,雖然微積分的威力有目共睹,但其邏輯結構的問題,始終讓數學家耿耿於懷。十九世紀,當數學家試圖把微積分及分析學嚴謹化時,他們愈來愈覺得所面對的其實是實數本身的問題。經由視覺觀察幾何圖形也許很容易了解函數連續的意義,但怎麼用數學的語言來表示連續的概念呢?實數軸是個連續直線,那麼其相應的實數的連續性又如何做嚴格的定義?極限為微積分的最重要觀念,那麼極限的意義又怎樣用數學來表示?這種種都牽涉到實數是什麼的問題。 在1872年左右,有好幾位數學家同時提出了實數系統建構的理論。他們都把有理數當做已知的東西,從而描述實數系統。他們描述的方法雖異,但從數學的結構觀點來看,所描述的卻是同樣的東西。 第一種描述方法是 R. Dedekind(1831∼1916年)提出的。如果在一直線上規定好 0 點及單位點 1,則有理數都可以依距離及正負對應到此直線上。如果我們在直線上砍一刀,在斷口左邊的所有有理數集合稱為 A,其右邊的稱為 B。若斷口正好是有理數,則此有理數可以任意規定屬於 A 或 B。A、B 這兩個有理數的子集合有下列兩個性質:一、A、B 都含有有理數,且 A 及 B 的聯集為有理數;二、A 中的有理數必小於 B 中的有理數。我們藉幾何直觀而得 A、B 這兩個集合,反過來,我們可以完全捨棄幾何,而考慮滿足上述兩個性質的有理數子集合 A、B。這樣的 A、B 稱為一個斷口,以 (A,B) 表之。Dedekind 說,(A,B) 就代表一個實數,而且實數的全體就是所有斷口的集合。如果 A(或 B)中有最大(或小)的有理數,則 (A,B) 代表的就是這個有理數。如果 A 中沒有最大,B 中沒有最小的有理數,則 (A,B) 代表的是一個無理數。無論如何,(A,B) 代表的是在直線上由其所決定的斷口。(當然不會有 A 中有最大,同時 B 中有最小有理數的情形。)為了完全脫離幾何直觀,我們還得定義兩個斷口 (A1, B1) 和 (A2, B2) 相加、相減、相乘或相除後應該是相應到那個斷口,同時也要定義兩個斷口的大小關係,這些其實都不難。 直觀上我們認為 Dedekind 的斷口會和直線上的點一一對應;另一方面,我們也可以證明有些斷口並不相對於有理數,也就是說 Dedekind 的實數系統確實是有理數系的擴張。如果把 Dedekind 的實數全體也分成 A、B 兩子集,而且也滿足上面兩個條件,我們一樣可以考慮斷口 (A,B)。那麼我們還能得到 Dedekind 實數系統的再擴張嗎?答案是否定的,因為我們可以證明:或者 A 含有最大的實數,或者 B 含有最小的實數,所以斷口還是在原來的實數上。這是實數的完備性,同時也表現實數的連續性。仔細研究 Eudoxus 的比例論(見《科學月刊》第十二卷第五期(1981)本欄)和 Dedekind 的實數系統,你一定發現它們有多麼的相似。Dedekind 自己也承認,他的理論源自 二千三百年前的比例論。
G. Cantor(1845∼1918年)和 C. Meray(1835∼1911年)提出另外一種描述實數的方法。一個有理數列 {xn},如果當 m、n 夠大時,|xm - xn| 就會小到任何預定範圍內,則 {xn} 稱為一個基本數列。如果把一基本數列相應的點標在直線上,則這些點終究會擠在一起。Cantor-Meray 希望他們的實數系統會使 {xn} 趨近於一實數,所以乾脆就讓 {xn} 代表一實數。但另一基本數列 {yn} 也可能趨近於同一實數。所以如果
Cantor-Meray 實數系統的最具體表示就是無窮小數。任意無窮小數
Cantor 在數學上的主要貢獻是集合論,而集合論最初最主要的突破就是把無窮元素的集合也分出大小。他的結論說:有理數的個數和自然數的個數一樣多(彼此之間有 1-1 對應),代數數的個數也一樣。這些集合的元素都可以按某種順序一個一個排列下來;實數就不然,這可利用實數的無窮小數表示法來證明。這個結果的主要意義是說:實數(也就是說超越數)的個數要比代數數多得太多。如果對實數的了解僅止於代數數,那麼看到的只是全豹的一斑。 Dedekind 或 Cantor-Meray 的實數建構看起來很抽象,但它們卻可經由已知的有理數來定義得清清楚楚。它們可用來澄清連續與極限的觀念,使微積分立於堅固的邏輯基礎上,使分析學的嚴謹化達 成目的。另一方面,抽象與具體原本是對立的,只要浸淫良久,仔細了解實數有趣而漫長的歷史,從各個角度接觸實數的性質,對實數的感覺就會顯得像它的名字一樣是實在而具體的。
|
對外搜尋關鍵字: .實數 .代數數 .Liouville .超越數 .Hermite .Lindemann .化圓為方 .Hilbert .Hilbert數學問題 .Hilbert第七問題 .Dedekind .Dedekind的斷口 .比例論 .Cantor |
|
|
|
|
(若有指正、疑問……,可以在此 留言 或 寫信 給我們。) |
|
|
|
EpisteMath (c) 2000 中央研究院數學所、台大數學系 各網頁文章內容之著作權為原著作人所有 |
| 最後修改日期:2/17/2002 |