談惠更斯級數 (第 2 頁)

　1│2│3│4│5　

談惠更斯級數（第 2 頁）

蔡聰明

首頁 | 搜尋

．原載於數學傳播第二十二卷第一期
．作者當時任教於台大數學系
‧對外搜尋關鍵字

平面幾何

先觀察畢氏定理的一個應用：

命題1：兩圓相切，半徑分別為 r₀ 與 r₁，並且跟 x 軸切於同側，切點為 A₀ 與 A₁，如圖 1，則

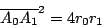$\begin{displaymath} {\overline{A_0A_1}}^2 = 4 r_0 r_1 \end{displaymath}$

(4)

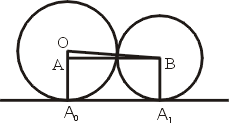
圖一

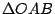證明：在直角三角形 $\Delta OAB$ 中

$\begin{displaymath} (r_0+r_1)^2 = \overline{A_0A_1}^2 + (r_0-r_1)^2 \end{displaymath}$

展開化簡立得(4)式。

命題2：在圖2中，兩圓與 x 軸之間又內切一個圓，其半徑為 r₂，則

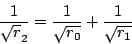$\begin{displaymath} \frac{1}{\sqrt r_2} = \frac{1}{\sqrt{r_0}} + \frac{1}{\sqrt{r_1}} \end{displaymath}$

(5)

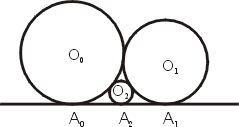
圖2

證明：由命題 1知，

$\begin{displaymath} \overline{A_0A_1}^2 = 4 r_0 r_1 \; , \quad \overline{A_0A_2}^2 = 4 r_0 r_2 \; , \quad \overline{A_2A_1}^2 = 4 r_2 r_1 \end{displaymath}$

又由

$\begin{displaymath} \begin{eqalign} \overline{A_0A_1}^2 &= (\overline{A_0A_2} + ... ...^2 + 2 \overline{A_0A_2} \cdot \overline{A_2A_1} \end{eqalign}\end{displaymath}$

所以

$\begin{displaymath} 4r_0r_1 = 4r_0r_2 + 4r_1r_2 + 2\cdot 2\sqrt{r_0r_2} \cdot 2 \sqrt{r_1r_2} \end{displaymath}$

整理化簡就得到(5)式。

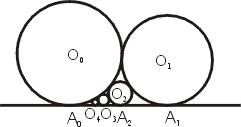
圖3

命題3：如圖3，不斷地作內切圓 O₂,O₃,… 下去，半徑為 r₂, r₃,…, 則

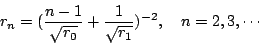$\begin{displaymath} r_n=(\frac{n-1}{\sqrt{r_0}} + \frac{1}{\sqrt{r_1}})^{-2}, \quad n = 2,3,\cdots \end{displaymath}$

(6)

證明：由命題2 知

$\begin{eqnarray*} \frac{1}{\sqrt{r_2}}&=&\frac{1}{\sqrt{r_1}}+\frac{1}{\sqrt {r_... ...}} =\frac{1}{\sqrt{r_1}}+\frac{3}{\sqrt{r_0}}\\ &&\cdots\cdots \end{eqnarray*}$

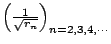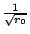由此看出 $\Big( \frac{1}{\sqrt{r_n}} \Big)_{n=2,3,4,\cdots}$ 為一個等差數列，公差為 $\frac{1}{\sqrt{r_0}}$ 。於是

$\begin{displaymath} \frac{1}{\sqrt{r_n}} = \frac{1}{\sqrt{r_1}} + \frac{n-1}{\sqrt{r_0}} \end{displaymath}$

從而

$\begin{displaymath} r_n = (\frac{n-1}{\sqrt{r_0}} + \frac{1}{\sqrt{r_1}})^{-2} \end{displaymath}$

推論：特別地，如果圓 O₀ 與 O₁ 的半徑皆為 1，則

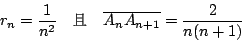$\begin{displaymath} r_n = \frac{1}{n^2} \quad \mbox{{\fontfamily{cwM0}\fontserie... ...nt \char 47}} \quad \overline{A_n A_{n+1}} = \frac{2}{n(n+1)} \end{displaymath}$

(7)

從而

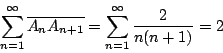$\begin{displaymath} \sum_{n=1}^\infty \overline {A_nA_{n+1}}=\sum_{n=1}^\infty \frac{2}{n(n+1)}=2 \end{displaymath}$

(8)

證明：由(6)式知

$\begin{displaymath} r_n = \Big( \frac{n-1}{\sqrt{1}} + \frac{1}{\sqrt{1}} \Big)^{-2}=\frac{1}{n^2} \end{displaymath}$

又由(1)式知

$\begin{displaymath} \overline{A_nA_{n+1}} = 2 \sqrt{r_nr_{n+1}} = \frac{2}{n(n+1)} \end{displaymath}$

我們注意到，(8)式可以由幾何圖形直觀地看出來，也可以採用下面圖 4 的「無言的證明」(proof without words)。

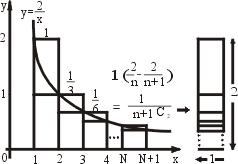
圖4

命題 4：在圖 5 中，兩圓 C₁ 與 C₂ 的半徑皆為 1，相切 P 點，並且切於 x 軸。在兩圓與 x 軸之間作一系列的內切圓 O₁, O₂, O₃,…，設其半徑為 r₁, r₂, r₃,…，直徑為 d₁,d₂,d₃,…，並且令 S_n = d₁ + d₂ + … + d_n，則

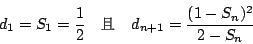$\begin{displaymath} d_1=S_1=\frac{1}{2} \quad \mbox{{\fontfamily{cwM0}\fontseries{m}\selectfont \char 47}} \quad d_{n+1}=\frac{(1-S_n)^2}{2-S_n} \end{displaymath}$

(9)

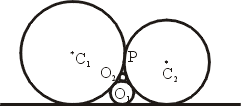
圖5

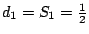證明：由(3)式知 $d_1=S_1=\frac{1}{2}$ 。又由畢氏定理知

$\begin{displaymath} (1+r_{n+1})^2 = 1^2 + \big[ 1-2(r_1+\cdots+r_n)-r_{n+1} \big]^2 \end{displaymath}$

於是

$\begin{displaymath} 4 r_{n+1}\big[ 1-(r_1+\cdots+r_n) \big] = \big[ 1 - 2(r_1+\cdots+r_n) \big]^2 \end{displaymath}$

從而

$\begin{displaymath} d_{n+1}=\frac{(1-S_n)^2}{2-S_n} \end{displaymath}$

推論：在命題 4 的假設下，我們有

$\begin{eqnarray*} && d_n = \frac{1}{n(n+1)} \quad \mbox{{\fontfamily{cwM0}\fonts... ...& \sum_{n=1}^\infty d_n = \sum_{n=1}^\infty \frac{1}{n(n+1)} = 1 \end{eqnarray*}$

習題：在圖 6 中，兩圓 C₁ 與 C₂ 的半徑分別為 r₁ 與 r₂ 相切，並且切於 x 軸。在兩圓與 x 軸之間作一系列的內切圓 O₁,O₂,O₃,…，設其半徑為 r₁,r₂,r₃,…。試證

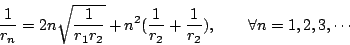$\begin{displaymath} \frac{1}{r_n} &=& 2n\sqrt{\frac{1}{r_1r_2}}+n^2(\frac{1}{r_2} + \frac{1}{r_2}), \qquad \forall n=1,2,3,\cdots \end{displaymath}$

(10)

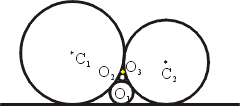
圖6

　1│2│3│4│5　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：簡立欣 ∕ 校對：簡立欣 ∕ 繪圖：張琇惠

最後修改日期：5/26/2002