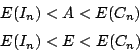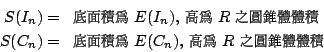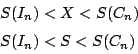| |
本文是譯自塞爾日.藍的演講記錄輯本《數學:挑戰中學生!》(MATH! Ecounter with High School Student),民國77年3月份的「數學傳播」曾刊過此書的第一篇,這是其中的另外一篇,讀者如果想對作者有更多的瞭解,可以參考當期的數學傳播,在那裡對此書及作者有一些簡短的介紹。-譯者
這個課程總共花了兩個小時的時間,前一小時在午餐前、後一小時在午餐後,對象是在巴黎大約九年級的一班學生,所以大概是在十四歲左右。因此,他們尚未習得畢達哥拉斯定理。
- 藍:你們在這堂課裡都做些什麼?幾何?代數?
- 全班:代數。
- 藍:幾何呢?
- 全班:有,一點點。
- 藍:所以你們也懂一些幾何?
- 全班:我們才剛開始。
- 藍:[指著一名學生]你知道π是什麼嗎?
- 學生:知道。
- 藍:那它是什麼呢?
- 學生:它是一個數,嗯……屬於幾何的……
- 藍:哦,是嗎?哪一個數?
- 學生:3.14……。
- 藍:3.14……?那麼π如何表示呢?
- 學生:???
- 藍:好。誰知道π如何表示?你,你叫什麼名字?
- 學生:克里斯多夫。
- 藍:好。克里斯多夫,怎麼表示呢?
- 克里斯:一個圓的圓周。
- 藍:那又是什麼樣的一個圓周呢?
- 克里斯:你指的是什麼意思呢?
- 藍:我的意思是,譬如給個π的函數。
- 克里斯:???
- 藍:你有一個圓半徑……
- 一個學生:哦!它是
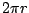
- 藍:很好!
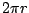 ,在這裡r是它的半徑。那麼,它的面積是多少呢? ,在這裡r是它的半徑。那麼,它的面積是多少呢?
- 這些學生:它是
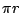 平方。 平方。
- 藍:對了,所以我們有兩個公式,像克里斯多夫所說的,π等於3.14……好,我不打算繼續討論這個問題,但是我想在更高一維度裡來做同樣的事情。假如我們到更高一維度去……你看,在我們討論圓周與面積之前,如果我們到更高一維度去,我們會得到什麼?
- 這個學生:一個球。
- 藍:對,一個球,我把它畫下來。那麼我們想對這個球做些什麼?
- 這個學生:體積。
- 藍:答對了,體積。你叫什麼名字?
- 這個學生:安。
- 藍:你知道半徑為r的球,它的體積公式是什麼嗎?
- 安:???
- 藍:誰知道這個公式?
- 全班:???
- 藍:好吧。一個圓的周長是
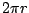 ,面積是 ,面積是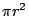 。但是球呢?會是什麼樣子? 。但是球呢?會是什麼樣子?
- 一個學生:π的平方乘上r的四方。
- 藍:不,讓我們回到盒子!假設我有一個正方形,邊長是r,那它的面積是什麼樣子?
- 全班:r平方。
- 藍:假設我有一個立方體,它的體積是什麼?
- 全班:r三方。
- 藍:你們已經做了一些推廣了嗎?
- 全班:一點點。
- 藍:好的,我們選擇一個邊長為a的立方體,那麼它的體積是a3,如果我做一延伸,在每一個方向上都乘上一個數r,那麼體積會變成什麼?安?
- 安:ra整個的三方。
- 藍:答對了,(ra)3,換句話說就是r3a3,對不對?每個人都了解嗎?所以我們可以說,如果我做一個延伸乘上一個數r,那麼體積就會改變了,如何改變?乘上一個數r3,對不對?好,現在讓我們繼續來看球體積會是什麼樣子?
- 蘇菲:
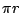 三方。 三方。
- 藍:哦!那並不是這麼顯然的吧?但是無論如何它一定會有r3這個數,因為我們把它延伸了。所以答案裡會有
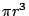 ,但在前面還有一個數,這個數等(4/3),這就是球的體積: ,但在前面還有一個數,這個數等(4/3),這就是球的體積:
你們還知道其它幾何圖形的體積嗎?還是你們只知道面積?這是你們所知道的第一個體積嗎?
- 全班:不,還有立方體!
- 藍:好,所以我今天想做的,就是要說明球的體積是(4/3)
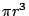 ,我想證明它。那麼,要怎麼證明它呢?沒有人知道嗎?首先我們要找出半徑為1的球體積,這比較簡單一點。半徑為1的球體積是多少?安? ,我想證明它。那麼,要怎麼證明它呢?沒有人知道嗎?首先我們要找出半徑為1的球體積,這比較簡單一點。半徑為1的球體積是多少?安?
- 安:(4/3)π。
- 藍:對了,(4/3)π,我們想證明半徑為1的球體積是(4/3)π,但是怎麼證明呢?
- 全班:???
- 藍:好吧,從我們知道的開始,例如圓柱體或盒子。如果有一個長方體盒子,底面積是B,高是h,那麼體積應該是多少?
- 蘇菲:底面積乘以高。
- 藍:答對了,B乘上h,在這裡我所選擇的底是一個長方形。但是如果我選擇一個不規則的形狀作為底面呢?任何形狀的底面,譬如像下圖
- 全班:也是一樣啊!
- 藍:是的,也是一樣,都是底面積乘以高。如果我有一個實心的圓柱體,它的底面是一個半徑為r的圓板,高是h,你[指著一名學生]……
- 翡蘿妮:???
- 藍:底部的面積是什麼?
- 翡蘿妮:???
- 藍:那是一個圓板,底部是一個圓板,圓板的面積是什麼?
- 羅卡夫:
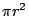 。 。
- 藍:所以圓柱體的體積是多少?
- 全班:
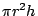 。 。
- 藍:很好,半徑為r高為h的圓柱體體積=pi r2h對吧?如果你知道圓板的面積是
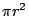 ,那麼圓柱體的體積就是 ,那麼圓柱體的體積就是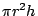 。每個人都同意吧?好,現在我們來看看球。我們要做什麼呢?我們要把球切成一塊塊的,切成我們所知道的,目前我們所知道的是圓柱體的體積。 。每個人都同意吧?好,現在我們來看看球。我們要做什麼呢?我們要把球切成一塊塊的,切成我們所知道的,目前我們所知道的是圓柱體的體積。
- 蘇菲:把它切成一半。
- 藍:如果我們把球切成一半,我們會得到像這樣的東西
- 蘇菲:我們可以把它再切成一片片,那底部將會是一個圓板。
- 藍:底部會是一個圓板,所以你就知道底部面積是
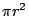 ,很正確。但是在最頂端仍然還有東西和圓柱體很不一樣的,那麼,我們怎麼做下去呢? ,很正確。但是在最頂端仍然還有東西和圓柱體很不一樣的,那麼,我們怎麼做下去呢?
- 安:再把它切成很多圓板。
- 藍:你實在非常聰明[笑聲]。對的,我們把它切成一片片,像這樣:好,你們知道畢氏定理嗎?
- 全班:不知道。
- 藍:如果我有一個直角三角形,像這樣:一邊是a,另一邊是b,第三邊斜邊是c,你們不知道 a, b, c 它們之間的關係嗎?你們從來都沒有看過它嗎?我們有 a2+b2=c2 你們從來都沒有見過這個嗎?
- 老師:明年才教!
- 學生范亞:為什麼要平方呢?
- 藍:為什麼要平方,這並不是那麼顯而易見的,必需要證明它!但這不是我今天要講的。所以我要求你們接受它,你們能接受它嗎?
- 全班:可以。
- 藍:好,現在我把這個球切成一片片,而且把它弄成一片片的圓柱體,像這樣。事實上,我是用了半個球,把這半個球切成一片片。每個人都看到這些薄片了嗎?如果我們從側面來看,它們看起來像是一些長方形,但是如果我把它們繞著垂直軸轉一轉,那麼我們就可以得到圓柱體了。而我們只要知道圓柱體的半徑和高 ,就可以知道它的體積了,是多少?
- 全班:
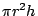 。 。
- 藍:好,現在我需要知道半徑和高。嗯,高要看圓柱體有多少個才能決定它的大小。我可以有5,或6,或更多個圓柱體,譬如我們畫一個有6個圓柱體的圖形。如果我把最底下的點當作原點0那麼第一個點的高度是多少?
- 全班:1/6
- 藍:下一個呢?
- 全班:2/6。
- 藍:再下一個呢?
- 全班:3/6。
- 藍:答對了,其它的點它們的高度分別是4/6,5/6,6/6。
- 全班:是的。
- 藍:那麼如果我有7小片呢?第一個點的高度會是多少?
- 全班:1/7。
- 藍:其它的呢?
- 全:班2/7,3/7,一直到7/7。
- 藍:如果我想把它一般化呢?我要怎麼說才對?
- 克里斯:
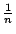 。 。
- 藍:
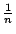 ?完全正確!一般而言我們會得到 ?完全正確!一般而言我們會得到 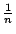 ,那麼第一個點會在哪裡呢? ,那麼第一個點會在哪裡呢?
- 全班:在
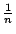 。 。
- 藍:下一個呢?
- 全班:在
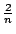 。 。
- 藍:再下一個呢?
- 全班:
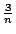 。 。
- 藍:最後一個呢?我們一直做到最後一個會是多少?
- 全班:
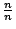 。 。
- 藍:答對了,這就是一般的情形。那麼每一個圓柱體的體積是多少?它的高等於多少?
- 一個學生:等於h。
- 藍:對,等於h,但h又是多少?
- 全班:……
- 藍:當我把這半個球切成6片,高是多少?
- 范亞:那要看你怎麼切啊!
- 藍:對,所有這些圓柱體都有相同的高度,你看到了嗎?
- 范亞:是的。
- 藍:高是什麼?如果我有6片的話?
- 范亞:1/6。
- 藍:對了,當我把它切成6片,那麼第二片的高也是1/6,其它的也都一樣,對不對?
- 全班:對!
- 藍:好,如果是6片,那麼每一片的高度是
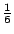 ,如果是 n 片,那麼每一片的高度該是多少? ,如果是 n 片,那麼每一片的高度該是多少?
- 全班:[全班一起]
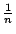 。 。
- 藍:非常好,
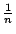 。現在我們來看半徑,半徑是多少?第一片的半徑是多少? 。現在我們來看半徑,半徑是多少?第一片的半徑是多少?
- 全班:r。
- 藍:對,是r,但r是多少?……好,我把這6個畫下來,第一個是r,第二個是r,第三個到最後一個都是r!但是半徑會改變的,是不是?那麼第一個半徑是多少?那是一個大圓的半徑,也就是球的半徑,這裡我把它當做1,記住,現在我們是要想辦法找出半徑為1的球體積。第一個圓柱體的半徑,我們寫成OA1,它等於多少?
- 全班:???
- 藍:我們實在不知道它是多少,不過它會比1小,同意嗎?
- 全班:同意。
- 藍:好,這裡我們要用到畢氏定理了。我們把第一個圓柱體畫下來!在圖形中我們有一個直角三角形OA1B1,而剛剛我們都同意了在直角三角形中,有這樣的結果a2+b2=c2,現在,在直角三角形OA1B1裡,a是什麼?
- 全班:是這個圓柱體的半徑。
- 藍:對了,是第一個圓柱體的半徑r1,那b是什麼?
- 菲力浦:是它的高。
- 藍:那高是多少?
- 菲力浦:1/6。
- 藍:對了,那麼c是什麼?
- 菲力浦:球的半徑。
- 藍:它等於多少?
- 菲力浦:嗯……1
- 藍:完全正確,所以我們就得到
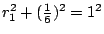 ,你同意這個式子嗎? ,你同意這個式子嗎?
- 菲力浦:同意!
- 藍:所以 r12 應該等於多少?
- 菲力浦:
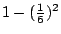 。 。
- 藍:答對了,非常好。現在我們來看第二個圓柱體。我把它畫下來。我又有一個新的直角形,OA2B2了
,在這個直角三角形裡,a是什麼?
- 菲力浦:是這個圓柱體的半徑。
- 藍:對,是第二個圓柱體的半徑 r2,那 b 呢?
- 菲力浦:是 A2B2。
- 藍:它等於多少?
- 菲力浦:
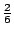 。 。
- 藍:很好,而 c 仍然是1,那麼 r22 應該是多少?
- 另一學生:r22 會等於
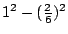 嗎? 嗎?
- 藍:你答對了!就是這樣。下一個是 r3,你們想 r3 會是多少?
- 這個學生:
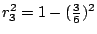 ? ?
- 藍:是的,你們懂了嗎?我們可以繼續下去囉?我們繼續看看r4,r5,r6,我把它寫下來[這個學生大聲複誦]。
現在我們對圓柱體的半徑有一些了解了。那麼這些圓柱體的高會是什麼?
- 卡琳:按順序來說應該是
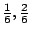 ,…… ,……
- 藍:不不,這是我們在計算半徑時所看到直角三角形的高。但是這些圓柱體都有相同的高,它等於什麼?
- 卡琳:1/6。
- 藍:答對了,很好,1/6。而半徑是隨著圓柱體改變的。這些半徑都有所不同,第一個半徑是r1,,第二個半徑是r2,第三個是r3,它們會變得愈來愈小,是不是?現在你們可以告訴我圓柱體的體積是多少了嗎?
- 李奇納:底乘以高。
- 藍:對,是
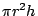 ,第一個圓柱體的半徑是r1,所以第一個圓柱體的體積是…… ,第一個圓柱體的半徑是r1,所以第一個圓柱體的體積是……
- 其他學生:[大家一起]
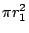 乘以1/6 乘以1/6
- 藍:那第二個圓柱體的體積是多少?
- 一些學生:
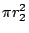 乘以1/6。 乘以1/6。
- 其他學生:
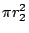 乘以2/6。 乘以2/6。
- 藍:誰說1/6的?
[一些人舉手]
誰說2/6的?
[另一些人舉手]
- 藍:不對不對!第二個圓柱體的高也還是1/6,是不是?所以第二個圓柱體的體積是什麼?它應該是
第三個圓柱體的體積呢?
- 李奇納:是
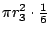 。 。
- 藍:答對了!下一個呢?
- 安:
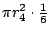 。 。
- 藍:對,不過r10xA141r2的平方我們一分鐘前已經找出來了,這些平方是多少?
- 諾拉:
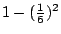 , ,
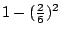 ,…… ,……
- 藍:所以如果我把這些圓柱體都加起來,我會得到什麼?……你,你叫什麼名字?
- 一個學生:藍生。
- 藍:哇,和我同姓![笑聲]好,所以我得到了這樣的和[藍一邊問學生一邊寫下來]第一個是什麼?藍生?
- 藍生:
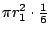 。 。
- 藍:而r12等於什麼?
- 藍生:
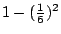 。 。
- 藍:好,所以第一個圓柱體的體積就是
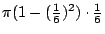 ,那麼第二個呢? ,那麼第二個呢?
- 藍生:
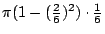 。 。
- 藍:第三個呢?
- 藍生:
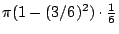 。 。
- 藍:好,我們繼續做下去,然後把這些體積加起來,就得到圓柱體的體積和=
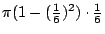 + +
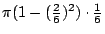 +…+ +…+
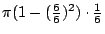 。現在假設我把6個小圓柱體改成7個小圓柱體,那麼我們得到的和會是什麼?
你,你叫什麼名字? 。現在假設我把6個小圓柱體改成7個小圓柱體,那麼我們得到的和會是什麼?
你,你叫什麼名字?
- 這個學生:希蘿麗。
- 藍:好,希蘿麗,和是什麼?
- 希羅麗:你必需把6改成7,就是
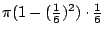
- 藍:很好,繼續下去最後一個是多少?
- 希羅麗:
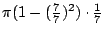
- 藍:現在我們可以改成 6, 7, 8, 9, 10,……如果我乾脆把它切成n片,那麼我們得到的第一個圓柱體的體積是多少?
- 希羅麗:
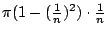
- 藍:太棒了!下一個呢?有沒有其它人會?
- 一個學生:
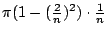
- 藍:對,繼續下去就像這樣子。最後一個會是什麼?(指著一名學生)你叫什麼名字?
- 這個學生:卡拉斯。
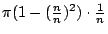
- 藍:答對了!所以這些圓柱體的體積和就是:
現在,如果 n 愈來愈大,這個和會變成什麼?它會很接近什麼?
- 全班:???
- 藍:我得到愈來愈多的圓柱體,像這樣這些圓柱體的體積會接近什麼?
- 菲力普:球的體積。
- 藍:[正把它寫下來]當n愈來愈大,圓柱體的體積和會接近半徑為1的球體積所以,現在問題變成:當n愈來愈大時,這個式子的右邊變成什麼樣子?
- 安:你可以把它算出來!
- 藍:你想直接把它算出來?好,可是怎麼算呢?
- 安:把一個個的體積算出來。
- 藍:對,這是當妳有任何特殊的數字的時候,像6或10。但如果是n怎麼辦?而且n又愈來愈大了?妳不知道n是什麼特別的數字,所以現在我們要做的就是當n愈來愈大時,怎麼把這個和算出來。不過我們要花午飯過後把它做出來,下午見了!
第二個小時
[全班於午餐後再回來上課]
- 藍:好了,我們又回來了,剛剛我們的問題是去找出半徑為1的球體積。我們已經證明了半個球的體積可以用
這樣的式子來接近它,而且當n愈來愈大時,它就更接近半個球的體積。在這個式子裡,我們可以看到每一項都有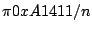 這兩個數,所以我們可以把它提出來,變成 這兩個數,所以我們可以把它提出來,變成
![$\pi/n[1-(\frac{1}{n})^2+1-(\frac{2}{n})^2+1-(\frac{3}{n})^2+\cdots+1-(\frac{n}{n})^2]$](img38.gif) 現在讓我們看看括弧裡的式子。我們看到有好多個1,到底有多少個呢? 現在讓我們看看括弧裡的式子。我們看到有好多個1,到底有多少個呢?
- 全班:n個。
- 藍:對,所以我就得到
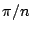 [n-一些要被減去的東西]什麼是我們要減掉的? [n-一些要被減去的東西]什麼是我們要減掉的?
- 李奇納:
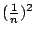
- 藍:答對了,還有呢?
- 李奇納:
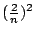
- 藍:很好,下一個是什麼?克里斯?
- 克里斯:
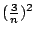
- 藍:對,一直到
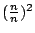 ,所以我們要減掉 ,所以我們要減掉
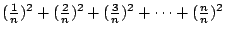 因此,如果我們把它全部寫下來,整個式子變成什麼?克里斯? 因此,如果我們把它全部寫下來,整個式子變成什麼?克里斯?
- 克里斯:
![$(\pi n/n-(\pi/n)\cdot[(\frac{1}{n})^2+(\frac{2}{n})^2+\cdots+(\frac{n}{n})^2]$](img45.gif)
- 藍:但是
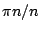 等於多少? 等於多少?
- 克里斯:π
- 藍:對,現在要減掉……
- 克里斯:
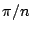 ,……嗯…… ,……嗯……
- 藍:對,繼續。
- 克里斯:乘以
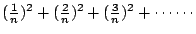
- 藍:很好,一直到
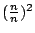 ,所以現在式子就變成 ,所以現在式子就變成
![$\pi-\pi[(\frac{1}{n})^2\cdot \frac{1}{n}+(\frac{2}{n})^2\cdot \frac{1}{n}+(\frac{3}{n})^2
\cdot \frac{1}{n}+\cdots+(\frac{n}{n})^2\cdot \frac{1}{n}]$](img48.gif) 而且當n愈來愈大時,這個式子就愈接近半個球的體積。現在,假設我最開始說的式子是對的,你們想這個括弧裡應該會接近哪一個數了
而且當n愈來愈大時,這個式子就愈接近半個球的體積。現在,假設我最開始說的式子是對的,你們想這個括弧裡應該會接近哪一個數了
- 全班:???
- 藍:半徑為1的半球體積我們假設它等於
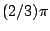 ,這裡我們又有這樣的式子 ,這裡我們又有這樣的式子
如果這個式子接近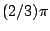 那麼括弧裡的和應該接近多少?你看到了嗎?我有一個π,而我又減掉π乘以一些分數,我希望最後剩下來 那麼括弧裡的和應該接近多少?你看到了嗎?我有一個π,而我又減掉π乘以一些分數,我希望最後剩下來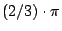 ,所以這個分數應該是多少? ,所以這個分數應該是多少?
- 一個學生:1/3。
- 藍:對。就是1/3,你叫什麼名字?伊莉莎白?她答對了!伊莉莎白答對了。括弧裡的式子接近1/3,非常好!這是我們必需要說明的。如果我們成功了,那我們就搞定了!好,我們把它寫下來,到目前為止,我們已經說明了圓柱體的體積和等於
所以我們現在要證明
會接近1/3,乍看之下,這好像是個很難解的問題。有一些平方,還有好多個n,它們的和是什麼完全不是那麼明顯可以看出來的,所以,我們該怎麼呢?
- 全班:???
- 藍:假如沒有平方,你認為你比較有可能把它算出來嗎?好,我們發現這個式子裡有一些數有平方,而我們不曉得怎麼做。這個問題看起來很困難,因此我們試著去思考一個類似,但比較簡單的問題,所以我們試試看沒有平方會是什麼樣子。假設我寫下來的式子裡沒有平方,它看起來會是什麼樣子?克里斯?
- 克里:
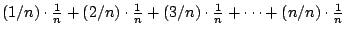
- 藍:答對了,現在我們有了一些分數的和,它們的分母是……伊莉莎白?
- 伊莉莎白:
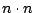 。 。
- 藍:對,你也可以說是n平方,不過你對了,我們可以把它寫成
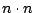 ,那麼分子是什麼? ,那麼分子是什麼?
- 伊莉莎白:
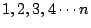 。 。
- 藍:對,那麼我要怎麼把這個和算出來?讓我們來畫個圖,我要用這樣的方法來解決這個問題。我畫一個邊長是1的正方形,而且把它切成一片片,我把它切成每一個邊長都是1/n的小正方形,像這樣在左下角的點我把他當作0,所以當我往右邊走的時候,我就得到了一些點1/n, 2/n, 3/n……,最後一個是什麼?……克里斯?
- 克里斯:n/n。
- 藍:很好,那它的前一個是什麼?
- 克里斯:(n-1)/n。
- 藍:對,再前一個呢?
- 克里斯:(n-2)/n。
- 藍:是的,垂直的那一邊從下到上我也做同樣的事。現在,我想找出
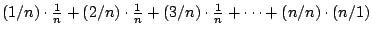
我們看看
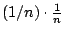 在這個圖裡,它應該是什麼? 在這個圖裡,它應該是什麼?
- 全班:???
- 藍:1/n 乘以 1/n 是什麼意思?那是一個邊長為 1/n 的正方形面積,所以在這個正方形中我畫出這樣一個小正方形,我們把它畫在這個圖形的左上角。下一個是什麼呢?那是 2/n 乘以 1/n,這表示什麼意思?
- 一個學生:是兩個小正方形。
- 藍:答對了,那是一個長為2/n,寬為1/n的長方形,我把它畫在第一個小正方形的下面。那3/n乘以1/n的呢?
- 全班:長3/n的長方形。
- 藍:那麼有(n-1)/n那一項呢?
- 全班:長(n-1)/n的長方形。
- 蘭:最後一個呢?
- 全班:長n/n的長方形。
- 藍:對,長是1,像這樣,把所有的長方形往一邊靠,所以圖形看起來就像是一個樓梯,而它們的和就是些樓梯的面積。現在如果我把n增加了,如果n變得愈來愈大,這些樓梯看起來會像什麼。
- 范亞:它會有很多階梯。
- 藍:嚴格來說,它是會有很多階梯,但這些樓梯的面積會接近什麼?當n愈來愈大的時侯?
- 一個學生:會接近這個正方形的一半。
- 藍:你叫什麼名字?
- 這個學生:里夫卡。
- 藍:你答對了!里夫卡答對了!我們把它寫下來:當n愈來愈大時,樓梯的面積會接近1/2,你們都同意里夫卡的說法嗎?都沒問題?好,那麼我們現在就要來看這個有平方的和了。剛剛我們已經看過一個比較簡單,沒有平方的和,而且我們處理這個比較簡單的問題,是把它看做一個個的樓梯,當n愈來愈大時,和就接近1/2了。這太好了,你們實在很棒哩![笑聲]
現在我們知道怎麼做下去了。我們可以回到那個有平方的和上了,好嗎?[全班都同意了]再把那個和重複一次:
我們怎麼做呢?[詢問的神色]好吧,我們看看這個和的某一項,例如
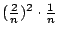 ,這是什麼?它指的是什麼意思?這是個體積,不是嗎?如果我把它看做是某個東西的平方乘上某個東西,我就可以把它當成是一個一邊長 ,這是什麼?它指的是什麼意思?這是個體積,不是嗎?如果我把它看做是某個東西的平方乘上某個東西,我就可以把它當成是一個一邊長 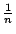 ,另一邊長是 ,另一邊長是 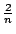 的盒子,你們同意嗎?好,現在有多少個盒子呢? 的盒子,你們同意嗎?好,現在有多少個盒子呢?
- 史第芬妮:n個。
- 藍:對,有n個。不過剛剛我們畫n個長方形的時候,我們把它畫在一個大正方形裡,現在我們有n個盒子,我們應該把它畫在什麼東西裡?
- 史第芬妮:一個大立方體裡有許多小立方體!
- 藍:[很欣賞地]哇!你有這種概念了!完全正確。所以我要畫一個邊長是1的大立方體,而且把它切成許多小立方體,每個小立方體邊長是 1/n。這是一個大立方體。現在我們要求的和裡頭的第一項是
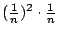 ,這指的是什麼?這指的是一個邊長為 ,這指的是什麼?這指的是一個邊長為 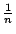 的立方體體積,像剛剛的小正方形一樣,我把它畫下來。下一個 的立方體體積,像剛剛的小正方形一樣,我把它畫下來。下一個
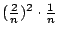 是什麼?這不是一個立方體了? 是什麼?這不是一個立方體了?
- 菲力浦:是一個長方盒子。
- 藍:對了,是一個長方盒子,有兩邊等於 2/n,高是 1/n,我把它畫在第一個小立方體的下方。那麼第三個
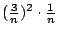 呢?伊莉莎白? 呢?伊莉莎白?
- 伊莉莎白:邊長為
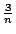 的長方盒子。 的長方盒子。
- 藍:對了,高仍然是
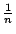 ,其餘的邊長是 ,其餘的邊長是 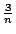 ,我們可以像這樣一直做到 ,我們可以像這樣一直做到 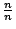 。所以有平方的和,我們也得到一個像樓梯一樣的圖形,但這是一個真實的樓梯,有體積;它們是三度空間裡的樓梯,就像現實生活中的一樣。現在,當 n 變得愈來愈大時,樓梯會接近什麼? 。所以有平方的和,我們也得到一個像樓梯一樣的圖形,但這是一個真實的樓梯,有體積;它們是三度空間裡的樓梯,就像現實生活中的一樣。現在,當 n 變得愈來愈大時,樓梯會接近什麼?
- 一個學生:1/3。
- 另一個:1/2。
- 藍:有其它意見嗎?
- 蘇菲:金字塔。
- 藍:啊!就是這個!這就是我想要聽到的答案。樓梯的形狀就接近一個金字塔,
你們都同意這一點嗎?我們怎麼得到這個金字塔呢?把這些長方體盒子的某一邊,頂點,
全都往最左邊靠,左上頂點和底下的正方形連起來,就得到一個斜的金字塔了。
看看這個立方體最上面的正方形,和左上方頂點相對的正方形有幾面呢?
- 里夫卡:三個嗎?
- 藍:對,有三個和它相對。這也就是說,我們會有三個像剛剛那樣的金字塔。
而且這三個金字塔把這一整個立方體全都填滿了。所以,這其中一個金字塔的體積等於多少?
- 范亞:2/3。
- 藍:不,在這個立方體裡有多少個金字塔?
- 范亞:三個。
- 藍:而立方體的體積是……
- 范亞:1。
- 藍:所以金字塔的體積是……
- 范亞:1/3。
- 藍:對了,1/3。現在讓我們回到高為(1/n)的樓梯上。當n愈來愈大,這些樓梯就會接近金字塔的形狀了,對不對?好,我把它寫下來:
當n愈來愈大時,樓梯的體積會接近體積為1/3的金字塔 這樣我們就搞定啦!這正是我們想要證明的。你們還記得我們從什麼地方開始的嗎?
我們從圓柱體的體積和開始,然後我們發現
括弧裡面的和有很多的平方。為了要算這個和,我們設法找一個類似但沒有平方的式子,
然後我們發現了一個平面的樓梯,當n很大的時侯它的面積接近1/2,現在和裡面有平方,
我們發現它是一個三度空間的樓梯,當n很大的時候,樓梯的體積就接近1/3,
因此圓柱體的體積和就接近
所以它等於多少?
- 伊莉莎白:
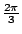 。 。
- 藍:所以我們就證明了半個球的體積是多少?
- 伊莉莎白:
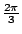 。 。
- 藍:因此整個球的體積是……
- 伊莉莎白:
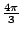 。 。
- 藍:這就是我們要證明的定理,我們贏了!
定理:半徑為1的球,體積是
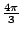 。 。
從剛剛那個方法裡,我們也得到了一些有關和的結果,而且知道當 n 愈來愈大時,它們的和會接近多少。
第一個,沒有平方的,是
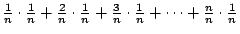 接近 接近 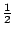
第二個,有平方的,是
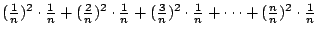 接近 接近 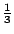
在這之後,下一個會是什麼?
- 克里斯:有三方的,
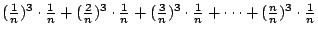 接近
接近 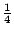
- 藍:誰說
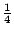 ?安,你認為如何? ?安,你認為如何?
- 安:不曉得,我不知道!
- 藍:伊莉莎白?藍生?
- 藍生:
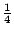 。 。
- 藍:前面兩個我們都證明過了,但是第三個我們還沒有證明,下一個呢?會是什麼樣子?
- 伊莉莎白:
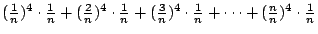 接近 接近 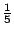
- 藍:太棒了!完全正確。這是一個定理,但是我們怎麼證它呢?
- 菲力浦:可是並沒有哪一個維度可以讓我們把
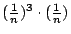 展開來,然後去找 展開來,然後去找 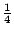 啊? 啊?
- 藍:很好很好,你已經完全了解剛剛我所講的了。所以我們現在遇到麻煩了!到三度空間為止,我們都是利用畫圖和計算樓梯體積的方法來處理問題,但假如我現在想要處理下一個問題……
- 一個學生:嗯,你可以想像……
- 藍:對了,你可以想像!而且你也必需這麼做!不過好像很不安全,感覺起來,好像不太保險。這樣引起了一些問題,而且事實上,我們也必需找其它的方法來解決,因為在更高維度裡,我們的直觀……太複雜了!像有立方的和,我們就必需在幾度的空間裡來做?
- 菲力浦:四度。
- 藍:對,下一個要在五度空間裡。但是現在我做的到底對不對,就無法再那麼確定了,因為我們已經打破直觀,所以你必需找一個代數上的方法來彌補高維度幾何直觀上的不足。這是可以做到的,不過我今天不打算談這個問題,但無論如何,這是真的。今天我所使用的方法,是把球切成許多小圓柱體,然後再把它們加起來。你們知道誰是第一個使用這個方法的人嗎?是阿基米得,你們聽說過阿基米得這個人嗎?克里斯……對,就是那個從浴缸裡跳出來,口裡喊著「我得到了!」的那個傢伙。你們聽過這個故事?他非常聰明,而他就是發明這種方法的人,我差不多是摹仿阿基米得來做的。所以現在我們做個結論:
半徑為 1 的球體積是
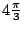
那麼半徑是 r 的球體積是多少?克里斯?利用延伸?
- 菲力浦:半徑為 r 的球體積等於
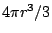 。 。
- 藍:對,你利用延伸得到了一個 r3,答對了,在這個班級裡你實在很棒!你對球知道得很多。我很少看到一個班級做得像你們這麼好,你們都很聰明。
你們還有其它問題嗎?數學的或其它方面的?[有一個學生舉手]什麼問題?
- 一個學生:用旋轉圓板的方法,你能不能把球的表面積算出來?
- 藍:好啊!你自己去試試看![笑聲]哦哦,可以可以,你可以做,不過……好,我們來試試看。利用圓板對垂直軸的旋轉來找出球的表面積。好,找它的圓周,或者我們只看一半圓周好了,是
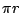 ,把它轉一圈,會得到什麼?你必需把 ,把它轉一圈,會得到什麼?你必需把 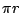 乘上某些東西。 乘上某些東西。
- 這個學生:乘上中間那個圓的圓周長。
- 藍:不過這樣會得到
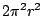 。 。
- 這個學生:哦!
- 藍:如果整個半圓的圓周都對一個半徑為 r 的圓之中心旋轉,那麼你的答案當然是正確的。但是你看,在最頂端和最底部,旋轉所對的圓比中間那個要小許多了,所以
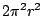 ,不會是正確的答案。但是如何得到正確的答案呢?你看到這個問題了嗎?有一個困難存在,你必需計算出每一個小片段對小圓旋轉之後會得到什麼結果。你的想法很好,不過你就必需要用到「平均圓」的概念了。這也有一個定理,不過現在做這個問題太複雜了,它是怎麼得來並不是那麼明顯的事。你們知道球的表面積公式嗎?就是 ,不會是正確的答案。但是如何得到正確的答案呢?你看到這個問題了嗎?有一個困難存在,你必需計算出每一個小片段對小圓旋轉之後會得到什麼結果。你的想法很好,不過你就必需要用到「平均圓」的概念了。這也有一個定理,不過現在做這個問題太複雜了,它是怎麼得來並不是那麼明顯的事。你們知道球的表面積公式嗎?就是
球的表面積 = 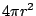
所以這個公式也告訴我們,必需乘上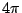 ,不會再乘上另一個π,而且可以用你的方法來證明它,不過這個問題太困難了,這也就是為什麼我喜歡用另一種方法的原因,不過這得另外找時間來說明了。 ,不會再乘上另一個π,而且可以用你的方法來證明它,不過這個問題太困難了,這也就是為什麼我喜歡用另一種方法的原因,不過這得另外找時間來說明了。
作者備註:
上這個班級的課讓我感到很愉快,這個主題對他們而言都還是相當新鮮的。一般而言,雖然老師們總想說明,不過最好還是等到10年級或是11年級再去證明比較好。另外,就像在本書的其它章節裡一樣,幾何常常能引起一些有趣的問題,可以導入代數中。我發現這個主題用來練習代數很不錯,可以幫助學生對n更加熟悉。球的表面積是下一堂課的主題。
譯者備註:
閱讀完這篇文章之後,不得不令人由衷地讚賞 Serge Lang 在處理數學教學上的能力。表面上看起來,他要教給學生的是如何求得球的體積,但是從過程中來看,他使數學課程活潑化,鼓勵並引導學生思考。我們可以看到,在這個課程當中,老師與學生互動的熱烈情況,而不是單調地只由老師詳細說明球的體積公式。Serge Lang 巧妙地以求得球體積為開端,很自然地促使學生逐步運用代數的方法來處理幾何的問題,把複雜的算式和熟悉且直觀幾何圖形結合起來。對一個中學生而言,這樣的處理方法無疑地最容易被接受了。
但是在阿基米得的著作中,並沒有看到阿基米得用 Serge Lang 所說的方法來求得球的體積。阿基米得所使用的方法,其基本概念是:利用圓的內接與外切正多邊形對垂直軸旋轉以逼近球體積,進而得到球體積公式。
假設半徑為 R 的球,表面積為 E,體積為 S;
阿基米得先證出
其中 A 為半徑等於 2R 之圓面積,即
再利用窮舉證法得 A<E,A>E 均為矛盾,故
其次,再說明
又證有
其中 X 為底面積是 E 高是 R 之圓錐體體積
他同上面的窮舉證法證得
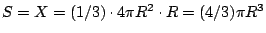 。 。
[詳細證明過程讀者可參考後面書目]
不過,就對立體圖形的直觀感覺而言,中國古代數學家祖沖之所使用的方法,可能更為直接。在此,我們提出一個簡單的介紹,讀者們可以作一番比較!
在《九章算術》第四章少廣章末,有這樣的一個問題:
今有積四干五百尺。問為立圓徑幾何?
答曰:二十尺
又有積一萬六千四百十八億六十六百四十三萬七十五百尺。問為立圓徑幾何?
答曰:一萬四干三百尺。
開立圓術曰:置積尺數,以十六乘之,九而一,所得開立方除之,即丸徑。
魏晉數學家劉徽指出這個方法是錯的:
……令圓冪居方冪四分之三,圓囤居立方亦四分之三。更令圓囤為方率十二,為丸率九,丸居圓囤又四分之三也。置四分自乘得十六分,三自乘得九,故丸居立方十六分之九也。故以十六乘積,九而一,得立方之積。丸徑與立方等,故開立方而除,得徑也。然此意非也。
他的意思是說,前人以為正方體與內切的圓柱體體積比為4:3(取圓周率為3),這是正確的,因為它們的體積比即為正方形與內切圓的比;但前人認為圓柱體與內切球體體積比亦為4:3,劉徽指出這是錯誤的,因為取兩者之截面,是兩個同心圓,並不再是正方形與內切圓,所以前人認為正方體與內接球體體積比為16:9是錯誤的。
劉徽認為:
……取立方基八枚,皆令立方一寸,積之為立方二寸。規之為圓囤,徑二寸,高二寸。又復橫規之,則其形有似牟合方蓋矣。……按合蓋者,方率也。丸居其中,即圓率也。……觀立方之內,合蓋之外,雖衰沒有漸,而多少不掩。判合總結,方圓相纏,穠纖詭互,不可等正。欲陋形措意,懼失正理。敢不闕疑,以俟能言者。
所以牟合方蓋和球體積的比才是正方形與內切圓面積的比,因此,如果要求得球的體積,應從解出牟合方蓋的體積著手,才是正途。但劉徽自認無法得到這個比,乃謙虛地留給後人作正確的計算。
有了這樣一個開端,南北朝時代的祖沖之終於算出牟合方蓋的體積,再進一步求得球的體積。對於他的方法,我們作一番敘述如下:
考慮如下圖之形狀:

牟合方蓋的分截
|
(1)在圖(1)中,此小立方體是球的外切大正立方體的 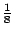 ,故小正立方體的邊長即為球之半徑 r。 ,故小正立方體的邊長即為球之半徑 r。
(2)將此小正立方體從橫豎兩面截為圓柱體的一部份,如圖(1),故整個小正立力體被分成四部份,如圖(2)、(3)、(4)、(5)。其中圖(2)便是劉徽所指的牟合方蓋的1/8,現在我們想把這個小的牟合方蓋的體積算出來。
(3)首先我們把這個已被切割的小正方體在高 h 處橫截,如圖(6)。在直角三角形ABC中,AB=r,BC=h,AC=小牟合方蓋截面正方形之邊長 a。
則由勾股弦定理知:a2=r2-h2= 小牟合方蓋截面面積。
(4)設其餘三部份截面面積為 S,則 S= r2-a2=
r2-(r2-h2)-h2;也就是說,不管在何處截面,S=h2 恆成立。
(5)接下來,取一個倒立的方錐,其邊長和高都等於 r,則在高為 h 的地方截之,其截面面積亦為 h2。
(6)由於剩餘三部份和的截面面積與方錐的截面面積均為 h2,高亦均為 r,故兩者體積也應相等,又方錐體積 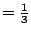 小立方體體積,由此可知小牟合方蓋的體積應為小正方體體積的 小立方體體積,由此可知小牟合方蓋的體積應為小正方體體積的 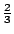 。故整個牟合方蓋的體積應為大正方體體積的2/3。 。故整個牟合方蓋的體積應為大正方體體積的2/3。
(7)因為牟合方蓋和內接球體積在等高處的截面積比為方和圓的比,故牟合方蓋和球的體積比為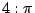 ,所以球的體積V為: ,所以球的體積V為:
雖然祖沖之和阿基米得均很巧妙地求出了球的體積,但是我們可以看到,他們所使用的方法及思考過程卻有著根本上的不同。在一味地追隨西方的數學思想脈絡之後,我們是否也應該承認,蘊藏在中國悠久的文化傳統中,有值得挖掘的數學寶藏。
參考書目
- 1. 李儼,《中國古代數學簡史》,台北九章出版社,1983。
- 2. 錢寶琮,《九章算術點校》,台北九章出版社,1984。
- 3. E.J. Dijksterhuis,《Archimedes》,Princeton:Princeton University Press,1987。
- 4. M. Kline,《數學史》上冊,台北九章出版社 ,1979。
|
|
對外搜尋關鍵字:
.畢達哥拉斯
.阿基米得
.祖沖之
.九章算術
.劉徽
.圓周率
|