黎曼Zeta--函數與 Bernoulli 數

．原載於數學傳播第十二卷第二期
．作者當時任職於中研院數學所副研究員

郭嘉南

對於實部大於1的複數 s，我們定義黎曼 zeta-函數如下：

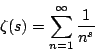
$\begin{displaymath} \zeta(s)=\sum_{n=1}^{\infty}\frac{1}{n^s} \end{displaymath}$

我們定義 Bernoulli 數為下面函數泰展開式中的係數 B_k：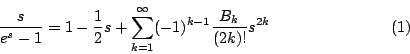

$\begin{displaymath} \frac{s}{e^s-1}=1-\frac{1}{2}s+\sum_{k=1}^{\infty}(-1)^{k-1}\frac{B_k}{(2k)!}s^{2k} \eqno{(1)} \end{displaymath}$

由(1)式，我們容易推出每一個 B_k 都是有理數。

我們可以對 $\zeta(s)$ 作解析延宕 (analytic continuation)，使得 $\zeta(s)$ 成為定義在整個複數平面上的半純函數 (meromorphic function)，並且只有在 s=1 這一點有一個 residue 為 1 的 simple pole。而且經過解析延宕之後， $\zeta(s)$ 滿足下面的 functional equation：

$\begin{displaymath} \pi^{-\frac{1}{2}s} \Gamma(\frac{1}{2}s)\zeta(s) = \pi^{-\frac{1}{2}(1-s)}\Gamma(\frac{1}{2}(1-s))\zeta(1-s) \end{displaymath}$

以上關於 $\zeta(s)$ 的性質，可以在 Ahlfors[1] 書裡找到，這不是這篇文章所要討論的主題。

黎曼 zeta-函數與 Bernoulli 數有如下重要的關係：

定理1：對任意正整數 $k \geq 1$ ，我們有

$\begin{displaymath} \zeta(2k) = \sum_{n=1}^{\infty}\frac{1}{n^{2k}} = 2^{2k-1}\frac{B_k}{(2k)!}\pi^{2k} \eqno{(3)} \end{displaymath}$

如果在(3)式取 k=1，則由於 $B_1=\frac{1}{6}$ ，我們得到

$\begin{displaymath} \sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{1}{6}\pi^2 \eqno{(4)} \end{displaymath}$

(4)式的結果是大數學家 Euler 所證明的，長久以來一直都深深地引人入勝。定理1 的結果當然比(4)式還要深入許多。定理1 有幾個不同的證明，一般都不太容易，譬如可以參考 Ahifors[1] 或 Titchmarsh[2]。這篇文章的目的是要給一個比較淺顯直接的定理1 的證明，當作學習心得，希望對閱讀這篇文章的讀者會有助益。

現在我們開始證明定理1

$\begin{displaymath} \mbox{{\fontfamily{cwM0}\fontseries{m}\selectfont \char 73}} f(s)=\frac{1}{e^s-1}\frac{1}{s^{2k}}(s\in \mathbf{C}) \end{displaymath}$

考慮下面的積分

$\begin{displaymath} I(N)=\frac{1}{2\pi i} \int_{\vert s\vert=(2N+1)\pi}f(s)ds \eqno{(5)} \end{displaymath}$

其中 N 為一正整數。我們不難證明存在一個與 N 無關的正數 $\delta>0$ ，使得在圓 $\vert S\vert=(2N+1)\pi$ 上，我們有

$\begin{displaymath} \vert e^s-1\vert \geq \delta \end{displaymath}$

所以當 $\vert s\vert=(2N+1)\pi$

$\begin{displaymath} \vert f(s)\vert=O((N\pi)^{-2k}) \end{displaymath}$

因此積分

$\begin{displaymath} I(N)=O((N\pi)^{-2k+1}) \eqno{(6)} \end{displaymath}$

另一方面，對於每一非零的整數 m，f(s) 在 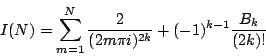$s=2m\pi i$ 這一點有一個 residue 為 $(2m\pi i)^{-2k}$ 的 simple pole。而且由(1)式，我們知道 f(s) 在 s=0 這點的 residue是 $(-1)^{k-1}\frac{B_k}{(2k)!}$ 。所以積分(5)式同時為

$\begin{displaymath} I(N)=\sum_{m=1}^{N}\frac{2}{(2m\pi i)^{2k}}+(-1)^{k-1}\frac{B_k}{(2k)!} \end{displaymath}$

現在令 $n\rightarrow +\infty$ ，由(6)式和(7)式，我們立刻得到

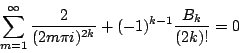
$\begin{displaymath} \sum_{m=1}^{\infty}\frac{2}{(2m\pi i)^{2k}}+(-1)^{k-1}\frac{B_k}{(2k)!}=0 \end{displaymath}$

所以

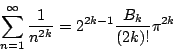
$\begin{displaymath} \sum_{n=1}^{\infty}\frac{1}{n^{2k}}=2^{2k-1}\frac{B_k}{(2k)!}\pi^{2k} \end{displaymath}$

因此定理1 得證。

結束本文之前，我們給幾個註腳。到目前為止，人們還不知道如何明確對正奇數 2k+1 表示 $\zeta(2k+1)$ 的函數值。定理1 只不過是在數論 (Number Theory) 的研究領域裡更一般的問題的一個特例。研究數論的數學家經常必須對某一類的函數，例如橢圓函數，Γ 函數等，在某些特定的點將其函數值明確表示出來。

: 1.L.V. Ahlfors,《Complex analysis》,3rd Ed. McGraw-Hill Book company.
: 2.E.C. Titchmarsh, 《The theory of the Riemann zeta-function》, Oxford University Press, 1951.

對外搜尋關鍵字：
．黎曼
．Euler


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：廖俊旻 ∕ 校對：黃怡碧

最後修改日期：4/26/2002