.原載於數學傳播第十卷第四期
.作者當時任教於中原大學數學系
董世平
|
.原載於數學傳播第十卷第四期 .作者當時任教於中原大學數學系 | |||
|
數學歸納法
董世平 |
|
在《數學傳播》第七卷第四期裡有一篇文章〈一些不可能無限延長的數學遊戲〉,這篇文章亦收在數學傳播季刊選輯《離散數學(二)》之內,文中介紹了一些看起來好像永遠玩不完的遊戲,這些遊戲裡有一個希臘神話中的九頭怪蛇難題,這個問題初看我們會覺得怪蛇的頭似乎越砍越多,要砍的話永遠砍不完,但卻被「證明」了一次砍一個,不論怎麼砍,遲早能將怪蛇的頭全部砍掉。現在我們就來談談這個結果的證明,使我們能多知道一些這個遊戲裡的數學。 上面的這個結果是 Kirby 和 Paris 所證明的,為要說明他們證明這個結果的動機,我們必須回到自然數的「皮阿諾公設」。 義大利數學家皮阿諾 (G. Peano) 於1889年以拉丁文印一本小書,整本書共有36頁,書名為《算數原理,以一個新方法表示》(The principles of arithmetic, presented by a new method)。 這本書中將自然數的一些性質抽象化而得到一組公設,盼望由這些公設藉著邏輯的演繹而得到所有自然數的性質,即將自然數「公設化」。 皮阿諾把每一個自然數的下一個稱為這數的「後繼者」(successor),用後繼者的說法, 這組皮阿諾公設可以寫成下面的形式(括弧裡是用符號的寫法,其中 n+ 表示自然數 n 的後繼者):
上面的第五個公設,也就是「數學歸納法原理」,為了加強對這原理的認識,我們將此一原理重寫成為下列的形式:
當我們使用數學歸納法來證明一些對所有自然數都成立的敘述時,我們常用下列方式,我們用 P(n) 來表示這個敘述,我們證明
我們用這個方法來證明時,有一點我們必須注意,即敘述 P(n) 是有一些限制的,不可以是任意的敘述。 徐道寧教授所著《數學歸納法》裡有一個這樣的例子, 用 P(n) 表示 n 粒沙子不成沙堆,用「數學歸納法」可得到「沙堆」不存在, 這個結果當然是不合理的,原因就是「沙堆」這一個觀念, 不是數學上能明確定義的,也就是無法用數學符號來表示「沙堆」這個觀念, 所以對敘述 P(n) 我們要求是可以用數學符號表示出來, 以避免一些無法正確定義的觀念如沙堆跑進來。
當我們討論自然數的性質,或是有關自然數的敘述,
這些大多可用「+」(加),「 p 是一個質數
再舉一個例子:兩連續數相乘必為偶數
這些可用上列符號所寫成的敘述,在邏輯中我們稱為「初等」(first order) 敘述,我們在數論中所遇到的敘述幾乎皆可用初等敘述來表示,我們也就問是否有關自然數的初等敘述皆可用初等皮阿諾公設來證明,此處所謂的初等皮阿諾公設即是用前四個皮阿諾公設,而當使用第五個公設「數學歸納法原理」時,敘述 P(n) 必須是一個初等敘述。 我們也許會覺得要藉著這五個公設來證明所有自然數裡的初等敘述,似乎太不夠了,但平常在數論裡的初等敘述,卻皆可用初等皮阿諾公設來證明,因此數學家們也就合理的猜想「所有數論裡為真的初等敘述,皆可用初等皮阿諾公設證明」。 但這個猜想在1931年被Gödel 有名的「不完備定理」(incompleteness theorem) 所證實是錯誤的,即有一些初等敘述是真的,但無法用初等皮阿諾公設來證明,而且即使加上再多的公設,只要有辦法分辨出是那些公設,那些不是公設,就始終有些敘述是真的,卻無法從這些公設證明。 在 Gödel 的證明中就給了一個這樣的敘述,雖然是真的,但無法用初等皮阿諾公設證明,但這些敘述的本質是由邏輯而來,在化成數論的形式,因此非常複雜。 自此數學家就開始尋找一個數學上簡單而有趣的定理,不要再用邏輯的方法,而這個定理是初等皮阿諾公設所無法證明的。 一直過了將近50年數學家才找到了這樣的例子,而開始所說的「九頭怪蛇」亦是找到的例子之一。 當我們看「九頭怪蛇」這個問題,我們是把它歸類於組合學裡,但這個結果的證明是用到一個邏輯家 Goodstein 於1994年所證明一個數論(廣義)上的定理,而 Goodstein 的定理也就成我們所知第一個數論上的初等敘述,是無法用初等皮阿諾公設證明。 現在我們來看看 Goodstein 的這個本身就相當有意思的定理。 設 m 和 n 為自然數且 n>1,我們定義「m 以 n 為底表示法」如下:
先將 m 寫成 n 乘冪的和,(若 m=266, n=2,那麼
266=28+23+21),
現在將每個指數寫成 n 乘冪的和,(如
266=223+22+1+21),
對指數的指數在繼續這個程序,
直到表示法穩定下來,(如
266=222+1+22+1+21)。
現在我們對 m 和 n 定義一個數 Gn(m) 如下︰若 m=0 令 Gn(m)=0,
否則令 Gn(m) 為將每一個 m 以 n 為底表示法中的 n 改為 n+1,
然後再減 1,如
G2(266)=333+1+33+1+2,
現在對每一個自然數 m 定義由 2 開始的Goodstein數列:m0=m, m1=G2(m0), m2=G3(m1), m3=G4(m2), 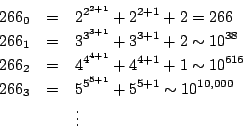
同理我們對每一個 m 皆可定義由 n (n>1) 開始的 Goodstein 數列。 相信當我們初看到這樣的數列時,我們都會覺得這數列增加的實在快,也就覺得這數列會這樣一直的增加下去,但令人不可思議的是 Goodstein 竟然證明了下面的這個定理:
這個定理若用數字真的去算的話,即使是很小的數字算起來也不得了,但我們可用 3,4,5 分別去算算 Goodstein 數列的前十項,(35=0),也許可以感覺到這個定理有可能是對的。我們也許會問這個定理是怎麼證明的?這個證明是用到集合論的一些結果,在此無法細說,只提到一個名詞,這個證明是用集合論中的「超限歸納法」(Transfinite induction),超限歸納法是一般數學歸納法的推廣,或許可說數學歸納法是超限歸納法的一個特例。 Goodstein 證明了這個定理:
|
對外搜尋關鍵字: .皮阿諾 .Godel .不完備定理 |
|
|
|
|
(若有指正、疑問……,可以在此 留言 或 寫信 給我們。) |
|
|
|
EpisteMath (c) 2000 中央研究院數學所、台大數學系 各網頁文章內容之著作權為原著作人所有 |
| 編輯:何岳勳 / 校對:陳文是 | 最後修改日期:6/22/2002 |