談研究年齡結構之數學模型

．原載於數學傳播第七卷第三期
．作者當時任教於交大數學系

談研究年齡結構之數學模型
Leslie's Model

許世壁

本文最主要的目的是介紹如何研究人口動力學 (Population Dynamics) 裏的一些有關年齡結構 (Age Strucure) 之問題。舉個例來說明：目前台灣人口中 0～5 歲有 x₁ 人，6～10 歲有 x₂人，……，76～80 歲有 x₁₆ 人。試問20年或100年後，這些人口的變化如何？還有每一個年齡分類 (Age class) 在總人口上的比例會不會很穩定地趨向某一個固定值？如果是的話，多快？就社會學、經濟學而言，這是一個很實際而且值得研究的重要問題。下面我們就要導出有關這個問題之數學模型──Leslie's Model。它同時也可以應用到其他生物，如魚類及昆蟲等。

首先，假設從現有的統計數據，我們能選擇出一個適當的單位時間 T，而後將人口分成 A 類。令向量 $\overrightarrow{V}_N$ 代表在第 N 期時（時間為 NT）人口裏的女性年齡結構（在此我們假設男性，女性人口數目相等），簡而言之令

$\begin{displaymath} \overrightarrow{V}_N = \left[ \begin{array}{c} V_{1,N} \\ \vdots \\ V_{A,N} \end{array}\right] \end{displaymath}$

在此，分量 V_k,N，k= 1,…,A 代表年齡介於 (k-1)T 及 kT 中間之女性總人數。譬如說應用到實際人口時，我們通常取 T=5 年，而且將人口分成 16 類，即 A=16，

: V_1,N = 在第 N 期時，介於 0～5 歲之女性總人數。
: V_2,N = 在第 N 期時，介於 6～10 歲之女性總人數。
: $\vdots$
: V_16,N = 在第 N 期時，介於 76～80 歲之女性總人數。

如果年齡超過80歲時，則我們不予討論。

下一步我們要做的工作是如何找出第 N+1 期的年齡結構向量 (Age structure vector) $\overrightarrow{V}_{N+1}$ ，與在第 N 期之年齡結構向量 $\overrightarrow{V}_N$ 之關係。假設下列的 b_k 及 m_k,k=1,…,A 為已知，

$\begin{eqnarray*} b_k &=& \mbox{{\fontfamily{cwM0}\fontseries{m}\selectfont \cha... ...inus0.1pt{\fontfamily{cwM1}\fontseries{m}\selectfont \char 170}} \end{eqnarray*}$

利用 b_n，m_k 及 V_k,N 之定義，我們可以導出下列關係式：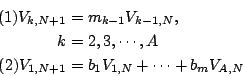

$\begin{eqnarray*} (1) V_{k,N+1} &=& m_{k-1} V_{k-1,N} , \\ k &=& 2,3,\cdots, A \\ (2) V_{1,N+1} &=& b_1 V_{1,N} + \cdots + b_m V_{A,N} \end{eqnarray*}$

其中(2)式說明了從第 N 期到 N+1 期所出生之女孩總數。所以，如果我們假設 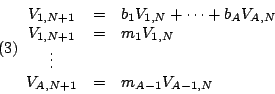$b_1,\cdots,b_A$ 及 $m_1,\cdots,m_A$ 這些非負之實數均可由人口之統計資料得到，則我們有下列式子

$\begin{displaymath} (3) \begin{array}{ccl} V_{1,N+1} &=& b_1 V_{1,N} + \cdots + ... ...N} \\ \vdots &&\\ V_{A,N+1} &=& m_{A-1} V_{A-1,N} \end{array}\end{displaymath}$

或者用矩陣之表示法，(3)式可改寫為

$\begin{displaymath} \begin{eqalign} (4)& \quad \overrightarrow{V}_{N+1} = M \ove... ... \end{array}\right] (\mbox{Reproduction Matrix}) \end{eqalign}\end{displaymath}$

如果，我們假設現在的年齡結構向量 $\overrightarrow{V}_0$ 。為已知，則由(4)式，我們得到：

$\begin{displaymath} (6) \quad \overrightarrow{V}_N = M^N \overrightarrow{V}_0 \end{displaymath}$

所以，我們將年齡結構的問題變成一個線性代數的問題：

當 N 很大時，向量 $M^N \overrightarrow{V}_0$ 如何變化？

為了解決這個問題，必須利用線性代數中有關固有值 (eigenvalue) 及固有向量 (eigenvector) 之觀念及其重要定理 Primary decomposition Theorem（參考[1]）。首先我們考慮 A x A 矩陣 M 之固有值 λ。從固有值之定義，λ 為 M 之特徵多項式 (characteristic polynomial) $f(\lambda) = \mbox{det} (M-\lambda I) =0$ 之根。通常特徵多項式很難算，但在這裏矩陣 M 有其特殊形式 (5)，所以利用降階展開行列式 det ( $M-\lambda I$ )，得到

$\begin{eqnarray*} (7) \quad f(\lambda) &=& \lambda^A - b_1\lambda^{A-1} - b_2 m_1 \lambda^{A-2} - \cdots - (b_A m_1 \cdots m_{A-1}) \\ &=& 0 \end{eqnarray*}$

因為 f(0) < 0 而且當 $\lambda >0$ 夠大時 $f(\lambda) > 0$ ，所以 $f(\lambda)=0$ 必有一正實根。事實上，因為矩陣 M 裏之係數皆大於或等於零，根據有名的 Frobenius定理（參考[2]）我們得知存在一固有值 $\lambda_0 > 0$ ，而且其他 A-1 個固有值 λ，滿足 $\vert\lambda\vert \leq \lambda_0$ 。現在，我們假設矩陣 M 滿足下列性質：

(H) 存在一固有值 $\lambda_0 > 0$ 而且其他 A-1 個固有值 λ，滿足 $\vert\lambda\vert < \lambda_0$ 。

在假設(H)下，我們可以用數值分析之方法 Power Method 實際地算出 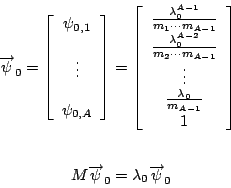$\lambda_0$ （參考[3]）。有了 $\lambda_0$ ，因為 $\lambda_0$ 滿足(7)式，我們可以檢查一下下列 $\overrightarrow{\psi}_0$ 為一對應於 λ 之固有向量；

$\begin{displaymath} \begin{eqalign} \overrightarrow{\psi}_0 = \left[ \begin{arra... ...rrow{\psi}_0 &= \lambda_0 \overrightarrow{\psi}_0 \end{eqalign}\end{displaymath}$

令 E₀ 為由向量 $\overrightarrow{\psi}_0$ 所產生之一維子空間， $E_0 \subset \mathbf{R}^A$ 。由線性代數的 Primary decomposition Theorem，我們可將 R^A寫成 R^A $= E_0 \oplus E_1$ ，其中 E₁ 是以對於固有值 $\lambda \neq \lambda_0$ 之固有向量 (eigenvectors) 或廣義固有向量 (generalized eigenvectors) 為其基底 (basis) 所組成的 A-1 維子空間。為了討論方便起見，我們就假設矩陣 M 之固有值為 $\lambda_0$ ， $\lambda_1$ ,…, $\lambda_{A-1}$ , $\lambda_i \neq \lambda_j$ 當 $i \neq j$ 而且令 $\overrightarrow{u}_i$ 為對應於 $\lambda_i$ 之固有向量。所以任何 $\overrightarrow{x}$ $\in$ ${\bf R^A}$ ，可唯一表為

$\begin{displaymath} \overrightarrow{x} = c_0 \overrightarrow{\psi}_0 + c_1 \overrightarrow{u}_1 + \cdots + c_{A-1} \overrightarrow{u}_{A-1} \end{displaymath}$

現令 P 為 E₀ 上之投影算子 (Projection operator on E₀)，即

$\begin{displaymath} P(\overrightarrow{x}) = c_0\overrightarrow{\psi}_0 \end{displaymath}$

令 $I(\overrightarrow{x}) = \overrightarrow{x}, \quad Q= I-P$
則 $Q(\overrightarrow{x}) = c_1 \overrightarrow{u}_1 + \cdots + c_{A-1} \overrightarrow{u}_{A-1}$

所以如果將 $\overrightarrow{V_0}$ 表為

$\begin{displaymath} \overrightarrow{V}_0 = c_0 \overrightarrow{\psi}_0 + c_1 \overrightarrow{u}_1 + \cdots + c_{A-1} \overrightarrow{u}_{A-1} \end{displaymath}$

則

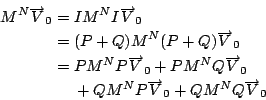
$\begin{eqnarray*} M^N \overrightarrow{V}_0 &=& I M^NI\overrightarrow{V}_0 \\ &=... ...\\ && {}+ QM^NP\overrightarrow{V}_0 + QM^NQ\overrightarrow{V}_0 \end{eqnarray*}$

從固有值，固有向量及 P,Q 之性質，可得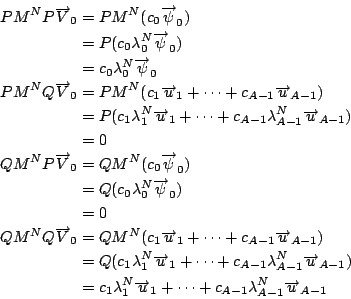

$\begin{eqnarray*} PM^NP\overrightarrow{V}_0 &=& PM^N(c_0\overrightarrow{\psi}_0)... ...{u}_1 +\cdots + c_{A-1} \lambda^N_{A-1} \overrightarrow{u}_{A-1} \end{eqnarray*}$

所以，

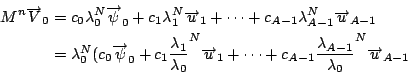
$\begin{eqnarray*} M^n \overrightarrow{V}_0 &=& c_0 \lambda^N_0 \overrightarrow{\... ...{A-1} \frac{\lambda_{A-1}}{\lambda_0}^N \overrightarrow{u}_{A-1} \end{eqnarray*}$

因為我們假設 $\vert\lambda_i\vert < \lambda_0$ ，i=1,…,A-1，所以當 N 很大時

$\begin{displaymath} (8) \quad M^N \overrightarrow{V}_0 \approx \lambda^N_0 c_0 \overrightarrow{\psi}_0 \end{displaymath}$

從(8)式，我們得到兩個結論

: (I) 年齡結構 (Age distribution) 是以 $\lambda_0$ 之速率成長
: (II)每個年齡分類 (Age class) 對總人口之比例是穩定地趨向一固定值

因為由(8)式

$\begin{eqnarray*} \lefteqn{ \frac{\mbox{{\fontfamily{cwM0}\fontseries{m}\selectf... ...^A_{j=1}\psi_{0,j}} = \frac{\psi_{0,k}}{\sum^A_{j=1}\psi_{0,j}} \end{eqnarray*}$

: [1] Smale & Hirsch :《Differential Equations,Dynamical System and Linear algebra》,Academic Press 1974.
: [2] S, Karlin & H. M. Taylor :《A first course in Stochastic Process》,Academic Press 1975.
: [3] K. Atkinson: 《An introduction to Numerical Analysis》,1978. John Wiley son.
: [4] F.C. Hoppensteadt: 《Mathematical method of Population Biology》.Courant Institute Lecture Note 1976.

對外搜尋關鍵字：
．人口動力學
．固有值
．固有向量
．Primary decomposition Theorem
．特徵多項式
．Frobenius
．basis
．Projection operator


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：康明軒

最後修改日期：4/26/2002