介紹兩本數學史 （註釋）

康明昌

 
註釋

...1
有關高木貞治 (T. Takagi) 的貢獻請參考 H. Hasse:《History of class field theory》收集在《Algebraic number theory》(編者：J.W.S. Cassels 與 A. Fiohlich)。
...2
在計算橢圓的部份弧長時， 我們得到形式如

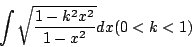
\begin{displaymath} \int \sqrt{\frac{1-k^2x^2}{1-x^2}}dx(0<k<1) \end{displaymath}

的不定積分。這就是一種橢圓積分。十八世紀的數學家發現這種橢圓積分不能用常見的函數表示出來。 更一般的，十九世紀的數學家把不定積分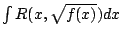 $\int R(x,\sqrt{f(x)})dx$通稱為橢圓積分， 其中f(x)是具有相異根的三次或四次多項式，R(u,v)是u,v的有理函數。 任意橢圓積分都可化成以下的標準形式:

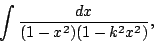
\begin{displaymath}\int \frac{dx}{(1-x^2)(1-k^2x^2)},\end{displaymath}


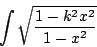
\begin{displaymath}\int\sqrt{\frac{1-k^2x^2}{1-x^2}}\end{displaymath}

或

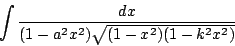
\begin{displaymath}\int\frac{dx}{(1-a^2x^2)\sqrt{(1-x^2)(1-k^2x^2)}}\end{displaymath}

令

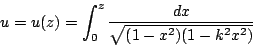
\begin{displaymath} u=u(z)=\int_0^z\frac{dx}{\sqrt{(1-x^2)(1-k^2x^2)}} \end{displaymath}

則u是z的函數。 若將其反函數記做sn，即z=sn u，則sn u是複數平面上雙週期的半純函數。

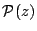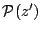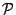一般情形下，所謂橢圓函數就是複數平面上雙週期的半純函數。橢圓函數可以寫成兩個θ函數的商，θ函數是Jacobi發明的。橢圓函數也可以表示成 $\mathcal{P}(z)$與 $\mathcal{P}(z')$的多項式，$\mathcal{P}$函數是Weierstrass發明的sn u的記號暗示這種函數很像正弦函數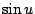$\sin u$。 像三角函數具有加法公式一樣，橢圓函數也滿足加法定律，這就是Abel's addition theorem。

把以上方法推廣，若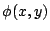$\phi(x,y)$是一個不可約的多項式，則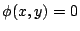$\phi (x,y)=0$決定一個黎曼面(Riemann surface)。 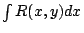$\int R(x,y)dx$稱為(在這個黎曼面的)一種Abel積分，其中R(u,v)是u，v的任意有理函數。 Abel函數是橢圓函數的推廣，橢圓函數是一個變數、兩個週期的半純函數， Abel函數是g個變數、2g個週期的半純函數，其中g是這個黎曼面的虧格數(genus)。不過從Abel積分做反函數得到的並不是Abel函數。

...3
法國大革命之前，Monge 是 Mezieres 軍校的考試官。有人曾勸他何不仿效他的前任 E. Bezout 寫一套六大冊的教科書。Monge 只寫了一冊就放棄了。但是在巴黎工藝學校與師範學校任教時，由於革命熱忱的激勵，他卻寫了兩本經典式的著作，一本是投影幾何的，一本是微分幾何的。其中那本投影幾何《Geometrie descriptive》在今日還是工程學上投影幾何的基本教科書。
...4
方程式 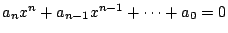$a_nx^n+a_{n-1}x^{n-1}+\cdots +a_0=0$ 有根式解的意思是，這些根都可用 a0,a1,…,an，經過加、減、乘、除、開方而得到。Abel 證明，如果這些係數 an,an-1,…,a0 是文字時(也就是以上方程式是文字方程式)，則這個方程式沒有根式解(若n=5)。對於每一個方程式，Galois定義一個根的置換群，方程式有根式解的充分必要條件是這個置換群是可解的(solvable)。Abel的定理是Galois定理的特殊情形。
...5
有關 Abel 函數，請看(註二)最後一段話。
...6
我認為要討論這個問題，有一些因素是不能忽略的，如：數學家逐漸專業化(代數學家、分析學家、幾何學家)，數學的內容與方法有某些根本的突破，中產階級的興起造成的教育普及，社會投資在基礎科學的研究增加，現代社會造成的激烈競爭。最後一個因素在十九世紀德國尤其明顯，如，Jacobi、Weierstrass、Klein在建立一些輝煌的理論之後，都精神崩潰，此後只能教書，不能繼續研究了。
...7
請參考F. Browder編的《Mathematical developments arising from Hilbert's problems》(美國數學會1976年出版)，其中有研究Hilbert問題的最新資料。
...8
根據 J. Dieudonne 的講法，十八世紀 90 % 以上重要的數學成就來自四、五個人，十九世紀來自三十多個人，二十世紀到目前為止不會超過一百個人。我認為，F. Klein 是肯定在十九世紀那三十多個人之中。
...9
這些度量衡就是今天的公制。當時有兩個主要的問題:如何選取基數與單位?基數要取l0進位或是沿襲以前的12進位?有人說，Lagrange認為採取12進位不如採取11進位，因為11是質數。另一個問題是單位長度該取多大，有兩個選擇，一個是把1米定為 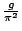$\frac{g}{\pi^2}$(g是重力加速度)，另一個是把1米定為赤道到北極之間距離的十萬分之一。最後採用第二個辦法，因為不久前Legendre才正確的測量出這個長度。Condorcet是百科全書派的一分子，他曾經用統計的資料來反擊那些反對牛痘的論調。他在《數學史》的唯一資料是，他大力提倡概率論，甚至主張把它用在法庭審判-數學的誤用!
...10
請參考J. G. Glimm, Mathematics program review, 登在Notices of American Mathematical Society, vol 30(1983), pages 4-6。
   


最後修改時間: 4/26/2002