| |
- ...註1
- 埃及人關於半徑為 r 的圓面積公式是
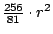 。 。
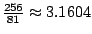 。見 Morris Kline 書,19頁。 。見 Morris Kline 書,19頁。
- ...註2
- 如果讀者不是像 Apollonius 那麼熟悉圓錐曲線的性質,他可以假設過 A 點的切線方程式是
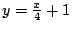 。我們在第四章第一節就可以導出這件事。 。我們在第四章第一節就可以導出這件事。
- ...註3
- 要得到
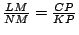 ,直接由各點的座標,當然也可檢查出來。 ,直接由各點的座標,當然也可檢查出來。
- ...註4
- 假設 (a,a2) 是拋物線 y=x2 上的任意點,如果讀者知道通過 (a,a2) 的切線方程式是 y=2ax-a2,很容易可以導出這個性質。我們在第四章第一節會說明如何求出這個切線方程式。
- ...註5
- 梯形 RkPk+1 是梯形
RkQk+1Pk+1Pk 的簡寫。
- ...註6
- 許多人相信 Euclid 是 Platonic school 的弟子。見 van der Waerden 書,P.196。
- ...註7
- 很有趣的是,Archimedes 完全意識到這些推論的瑕疵。將近二千年後的 Leibniz(萊布尼茲)遇到同樣的情形,卻毫無意識到這些推論的不嚴謹性,見 van der Waerden 書,P.214。
- ...註8
- 這是所謂 Pell equation。其歷史與解法可參看任何一本初等數論的教科書。許多人相信 Archimedes 並沒有把這個方程式的答案解出來。
- ...註9
- van der Waerden 書第八章與 Morris Kline 書第八章詳盡的討論希臘數學衰退的原因。
- ...註10
- Struik 書 P.48,對於 Platonic school 與 Democritus' school 的不同,有相當新穎的說法。
- ...註11
- Archimedes 這些方法寫在一本《the Method》的小冊子,在 Newton(牛頓)與 Leibniz(萊布尼茲)時代已經失傳。直到1906年,這本小冊子在君士坦丁堡 (Constantinople) 才被人們發現。見 van der Waerden 書,P.212。
- ...註12
- 或者我們知道通過五點的切線方程式。
- ...註13
- 為了使我們的圖形清楚起見,上述的補助線沒有畫出來。但是讀者只要利用「拋物線的面積(第二個方法)」中拋物線切線的性質,再配合相似形關係,就可證明
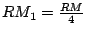 。 。
- ...註14
- (2)是由(1)利用「Eudoxus 性質」得到的。二十世紀的讀者已經具備了無窮等比級數的工具,由(2)就可導出
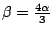 。但是 Archimedes 根本不知道什麼是無窮級數? 。但是 Archimedes 根本不知道什麼是無窮級數?
- ...註15
- 與上一節利用「Eudoxus(或Archimedes)性質」一樣。
- ...註16
- 讀者如果自己想不出如何利用槓桿原理發現這個定理,請參考 van der Waerden書P.214。
- ...註17
- 本章的情節是作者自己杜撰的。有關數學的部份,全部是有憑有據的;有一部份地方使用解析幾何是為了討論方便,Archimedes 是不知道如何把幾何圖形用代數方程式表示出來的。
|
|
|
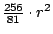 。
。
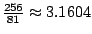 。見 Morris Kline 書,19頁。
。見 Morris Kline 書,19頁。
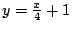 。我們在第四章第一節就可以導出這件事。
。我們在第四章第一節就可以導出這件事。
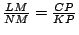 ,直接由各點的座標,當然也可檢查出來。
,直接由各點的座標,當然也可檢查出來。
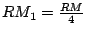 。
。
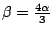 。但是 Archimedes 根本不知道什麼是無窮級數?
。但是 Archimedes 根本不知道什麼是無窮級數?