上頁　1│2│3　次頁

機率名題二則漫談 （第 2 頁）

戴久永

 

首頁 | 搜尋

．原載於數學傳播第四卷第四期
．作者當時任教於交大運輸工程與管理學系

•註釋
•對外搜尋關鍵字
 
伯特朗選票問題

(一)某班級有 25個學生，有甲乙二生出馬競選班代表，選舉秘密投票方式，開票的結果，其唱票順序如下：甲甲乙甲乙、甲甲乙甲乙、甲甲甲乙甲、甲乙乙甲乙、甲甲乙乙乙。

在宣佈選舉完畢後，丙生說「我注意到甲的票數總是領先，這似乎很神奇。」丁生回答說：「一點也不神奇，最後的結果是 14 比 11，甲獲勝，既然是甲贏，自然很可能他的票數一路領先」。

你贊同丁生的意見嗎？想想看！然後再做一下實驗，看看你能由實驗中發現什麼現象。做 25 張小紙條，14 張寫上甲，11 張寫上乙，然後把它們放入一容器內混合。把小紙條一張張由容器中抽出，如上題所示一一順序記下結果。如果是數人同時進行這種實驗，每人應保留其記錄，因為以後還用得著。查驗的結果，甲的票數仍是一路領先嗎？

一個簡單的實驗方法是：若甲得票記為 +1，乙得票記為 (-1)，應用這種數值，把你的票一一加起來。因此，上例的結果為

1,2,1,2,1,2,3,2,3,2,3,4,5,4,5,6,5,4,5,4,5,6,5,4,3

把你的結果和以上的結果比較，當你查驗完畢後，或許也可以和班上同學比較一下，然後再回想一下丙，丁的話，你贊成誰的意見？

下列問題可以幫助你試查你的想法是否正確：

1、若甲永遠領先，則第一票應為誰的票，第二票又如何？

2、在開出兩票後，甲領先的機率為若干？

3、在開出三票後，甲領先的機率為若干？

4、你對甲永遠領先的機率的結論為何？

法國數學家伯特朗（Joseph Bertrand, 1822∼1900）研究了一個選舉問題。若我們獲知選舉的結果，我們能求出於開票唱票時，當選人一路領先的機率嗎？

因此，在我們的問題中，我們要問，若已知開票結果為 14 比 11，則甲一路領先的機率為若干？

甲是否一路領先，得視 14 張甲和 11 張乙的安置序列而定，我們稱每一可能的安排為一種「順序」。(ordering)。

如果由容器抽出的選票每張大小都相同，用相同摺法並且攪混得很好。我們就可以假設所有可能的順序為相同可能，我們將做這樣的假設。

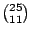現在我們想一下問題：共有多少相同可能的順序？答案是 ${25 \choose 11}$，即 4457400。

我們的問題有兩點令人感到驚奇的地方。第一、它的答案非常簡單。第二、它並不難發現答案，而且明瞭為什麼如此。

我們如何開始下手呢？想想看，看看你所建議的方式是不是和下節所採方式相同。

當一個問題看起來似乎很困難的時候，試試一個類似而簡單的形式必然有所幫助。我們先假設 5 人投票，甲獲勝的比數是 4 比 1。

把所有 4 甲 1 乙的不同順序排列出來，然後看甲是否一直領先？

順序 甲一路領先嗎?
甲甲甲甲乙 是
甲甲甲乙甲 是
甲甲乙甲甲 是
甲乙甲甲甲 否
乙甲甲甲甲 否

注意：我們有 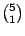${5\choose 1}$ 種可能順序，對應於 5 種選擇乙的方法。

另外一個方法是畫個圓圈，把選票寫在圈上。

如果由位置 1 開始，順時針方向移動，我們得到甲甲甲甲乙。上表所列每一順序相當於每一不同的啟始點。

在以上 5 種順序中，甲一路領先有三種，因此甲領先的機率為 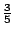$\frac{3}{5}$。讀者不妨試一下 3 比 2 的情形。

習題
1、若有3甲2乙，則共有多少種可能順序？

2、任選一種3甲2乙的順序，將3甲與2乙寫於圓上，使得當你自1號位置順時針方向移動，可得到你所選的順序。每次由不同點開始順時針移動列出所有你可得的順序。

3、在以上所有順序中，由那幾個為啟始點可得出一路領先的情形？

4、你在第2題中所得的順序已包含所有由3甲2乙的可能順序嗎？若不是，任選一種不在你已列的順序，同樣再畫個圓，將3甲與2乙寫於圓上，並且再列出所有你可得的順序。

5、在第4題所得的順序中，有多少個是甲一路領先的情形？

6、在3比2的情形下，甲一路領先的機率為何？

7、若為5比0，則甲一路領先的機率又為何？

(二)我們把結果摘錄如下：

得票 P(甲一直領先) 出票數 使用圈數 啟始點數
4比1 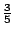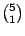$\frac{3}{5}$ ${5\choose 1}$=5 1 3
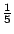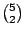3比2 $\frac{1}{5}$ ${5\choose 2}$=10 2 1

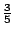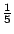注意到上表中的啟始點數指的是一圈上「甲一直領先」的啟始點數，又在上表中，第二列甲得4票乙得1票，甲一路順先的機率為 $\frac{3}{5}$。3得自何處？5得自何處？你能看得出型式 (pattern) 嗎？再看一下第二列中 3、2 和 $\frac{1}{5}$，它們能配合你的型式嗎？

現在，或許你已看出一種法則似乎較為合用。

令 X = 甲的得票數，Y = 乙的得票數。

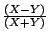得票 P(甲一直領先) X Y X-Y X+Y $\frac{(X-Y)}{(X+Y)}$
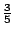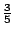4比1 $\frac{3}{5}$ 4 1 3 5 $\frac{3}{5}$
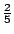3比2 $\frac{2}{5}$ 3 2 1 5 $\frac{1}{5}$

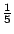由第二行與最後行相較， $P(\mbox{{\fontfamily{cwM7}\fontseries{m}\selectfont \char 66}\hskip 0.0pt plus0... ...1pt{\fontfamily{cwM0}\fontseries{m}\selectfont \char 108}})=\frac{(X-Y)}{(X+Y)}$ 至少，這個公式適於得票4比1和3比2的情形。

習題
8、本公式適用於5比0的情形嗎？

9、本公式適用於3票而得票而得票為2比1的情形嗎？

下圖為第一節所提25票的情形，請仔細研究一下本圖。


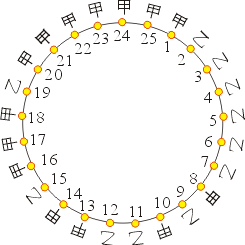
圖二

如果你由 1 開始順時針方向移動，則甲並非一路領先（事實上，在第二票時，二人平手）。但是如果由 13 開始順時針移動，則甲為一直領先，另外由 16、17 開始也是甲一路領先。

習題
10、現在請你把你的記錄取出，把甲、乙依次寫在一圓上，共有多少種情形是甲一路領先？

(三)現在我們將圖二仔細研究一下，由 1 開始甲之後緊接著是乙，而 1+(-1)=0，即甲於第二票時就失去領先的優點，其他在啟始點為 8、10、14 和 18 均為甲之後緊接著乙，把這些情形畫圖標明。


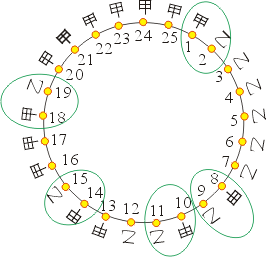
圖三

把這些對除去，則圖三變成如圖四情形：


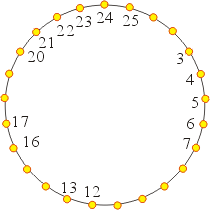
圖四

在圖四中，如果順時方向移動，還有其他甲之後緊接著乙的情形嗎？是的，甲在25和乙在3。把這一對除去。再繼續順時移動，甲在24和乙在4。也把這一對除去。如此繼續除去，23和5，22和6，21和7及20和12。見圖五：


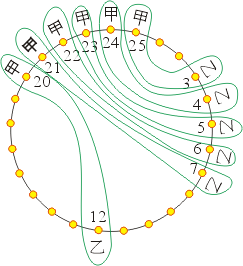
圖五

那些位置未被刪除？13、16和17，但是我們發覺這些位置正是給出甲一路領先順序的啟始點。

這種解釋是否提供了一些便於推廣的暗示？加果我們把選票依開票先後以順時方向寫於圖上．然後刪除當選人之後按著為落選人的成對，如此不斷刪除下去，最後所剩的就是當選人一路領先的啟始點位置。倘若你不相信，不妨再多試一下並且想得深入一點。

每次會剩下多少個位置呢？恰為當選票數與落選票數的差，即恰為 x-y。

回到得票比數為3比2的情形。我們發現必須兩個圓方才足以把所有可能順序完全列出，每一圓有5個順序。

\begin{eqnarray*} \mbox{{\fontfamily{cwM2}\fontseries{m}\selectfont \char 15}\hs... ...eries{m}\selectfont \char 98}}} &=& \frac{1+1}{5+5}=\frac{1}{5} \end{eqnarray*}


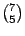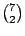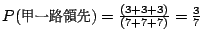或許你可以試著猜想一下若 7 票而甲與乙得票為 5 比 2 的情形。在本例中，總共有 ${7\choose 5}$ 或 ${7\choose 2}$ 種順序，我們需要 3 個圓才足以把所有可能順序全部列出（每圈有 7 個順序）。每圈有 (5-2)=3 個為甲一路領先的啟始點。因此似乎在本例中 $P(\mbox{{\fontfamily{cwM7}\fontseries{m}\selectfont \char 66}\hskip 0.0pt plus0... ...}\fontseries{m}\selectfont \char 108}}) = \frac{(3+3+3)}{(7+7+7)} = \frac{3}{7}$，換言之，又是 $P(\mbox{{\fontfamily{cwM7}\fontseries{m}\selectfont \char 66}\hskip 0.0pt plus0... ...1pt{\fontfamily{cwM0}\fontseries{m}\selectfont \char 108}})=\frac{(X-Y)}{(X+Y)}$。

習題
11、一個十人委員會環坐於一圓桌，在表決其提案時，得7票贊成，3票反對，試問當主席問到每一人的意見時，贊成票數總是領先反對票數的機率為多少？

12、甲主持一個小組會議，小組組員的位置如下圖所示。除了乙之外，其他人對某議案的態度甲都已事先知道。甲深知乙的個性，如果甲問每一人的意見時，贊成人數領先的話，則當問到乙的意見時，乙必定投贊成票。甲希望能得到他所有能得的贊成票，試問甲該自那一位置問起，才會使得在叫到乙之前呈贊成票領先的情勢。


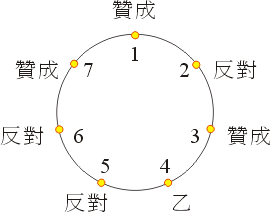
圖六

13、在一個家庭宴會中男孩和女孩圍著圓桌坐如圖七所示。當吃完晚飯後，女主人說「男仕們請帶著坐在你左邊的小姐到院子來玩乒乓混合雙打。」 試問有那些男仕沒有女伴？


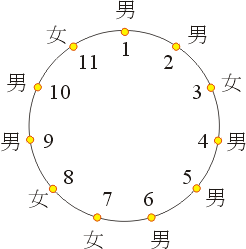
圖七

14、王家吃飯時圍著圓桌而坐，王太太於飯後拿出水果，3 片西瓜和 3 片鳳梨放於一盤上，試問籃子應自那一位子開始順時方向傳遞才能使坐於 1 號位置的王先生分到他喜歡的西瓜。（圖八號上的標字表示坐該位子的人的偏好）


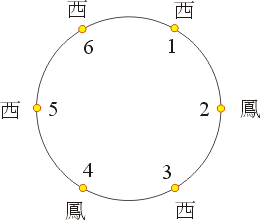
圖八

在本題中，我們用圓圈來幫助列出可能的順序。例如在 5張選票的問題中，用一個圓圈寫上5個位置，這個圈給我們5個可能的順序。同樣的，25張要的圓圈給我們25種可能的順序。

我們能一直假設事情如此的單純嗎？再多看一個題目可能有助於你回答最後這個問題。

習題
15、設有6票的選舉──甲得4票，乙得2票──共有多少可能順序？
16、任選一種可能順序，即其標於一圓周上，並且寫出所有不同順序，然後再寫出一種不在你已列出之內的順序，再標於同一圓周上，寫出所有不同的順序，如此不斷地做，直到得出所有可能順序為止。

(四)在第十六題中，你畫出三個圓。或許你所畫出的圓並不全和如下三圓相同，但它們實際上並沒有什麼差異。


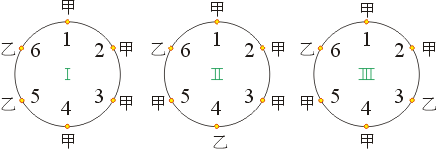
圖九

由圖九(I)中，你可得6種不同可能出象，其中有2種為「甲一路領先」，即啟始點1、2。

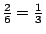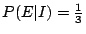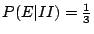假設你主持一項選舉，有人告訴你結果為圓I中6種出象之一，則甲一路領先的機率為 $\frac{2}{6}=\frac{1}{3}$。現令 E =「甲一路領先」的事件。I= 圓I中順序所構成的事件。II= 圓II中順序所構成的事件。III= 圓III中順序所構成的事件。則圓I中甲一路領先的機率可改寫為 $P(E\vert I)=\frac{1}{3}$，這是一個條件機率，同法可得 $P(E\vert II)=\frac{1}{3}$。

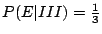我們再來看一下圓III，它僅有3種不同出象。例如以1為啟始點與以4為啟始點所得順序全然相同。啟始點1、2、3各得不同順序，其中只有啟始點1為甲一路領先，因此 $P(E\vert III)=\frac{1}{3}$。

我們可以把15種可能出象以下表表示：


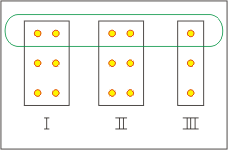
圖十

E 為三個集合 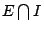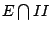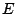$E\bigcap I$,$E\bigcap II$,$E\bigcapIII$ 的聯集，這三個集合為互斥。 因此，

\begin{displaymath}P(E)=P(E\bigcap I)+P(E\bigcap II)+P(E\bigcap III) \: .\end{displaymath}

至此，我們可以應用條件機率的知識：

\begin{displaymath}P(E\bigcap I)=P(I)P(E\vert I)=\frac{P(I)}{3}\end{displaymath}

同理

\begin{eqnarray*} & P(E\bigcap II)=\frac{P(II)}{3} ,\quad P(E\bigcap III) = \fr... ...+\frac{P(II)}{3}+\frac{P(III)}{3} = \frac{P(I)+P(II)+P(III)}{3} \end{eqnarray*}


P(I) 為任一順序得自圓I的機率，P(II) 為任一順序得自圓II的機率，P(III) 為任一順序得自圓III的機率。

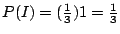
因此 P(I)+P(II)+P(III)=1 所以 $P(I)=(\frac{1}{3})1=\frac{1}{3}$

在本例中，得票為4比2，並非每個圓圈都有6種不同出象。但是第4節的理由仍然適用於每一圓圈，並且不同圓相關的條件機率聯合起來仍給出與前相同的結果，較複雜的情形只是多用些圓，最後結果仍然不變。即 X>Y 時，

\begin{displaymath}P(\mbox{{\fontfamily{cwM7}\fontseries{m}\selectfont \char 66}... ...ly{cwM0}\fontseries{m}\selectfont \char 108}})=\frac{X-Y}{X+Y} \end{displaymath}

   

上頁　1│2│3　次頁

 回頁首
 
（若有指正、疑問……，可以在此 留言 或 寫信 給我們。）
EpisteMath

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有


編輯：黃信元 最後修改日期：4/26/2002