對數與約翰．納皮爾 (John Napier)

．原載於數學傳播第三卷第四期
．作者當時任教於清大數學系

賴漢卿

對數這個名詞，對國中、高中的同學來說都不會陌生，因為他們要學常用對數。進到大學上微積分時，以 e 為底的指數與對數函數更具基本的重要性。我上課，每次說到這裏總要簡單提一提有關對數的故事，以引起學生的興趣。今年我上微積分課時，學生提議將這些故事寫出來好讓較多的學生分享此故事。寫與講稍有不同，蓋寫出來總得要有系統及根據、講則可以較不嚴格，然應學生的希望，乃花些工夫做個報導。

今天我們所用所講的對數為常用對數或自然對數，與最早 Napier 的對數稍有出入，唯其來源的精神及其性質可說來自 Napier，祇是形式不同而已。現在就來介紹 Napier 其人及其發明之對數法則。

John Napier, 1550～1617

我們知道當一個人想計算大數之積與商時，都常利用對數方法，求其近似值。其起源可遠溯 Kepler（1571～1630）研究天體運動學時他遇到許多非常大的數值計算，但他要求的是有效的近似值，因之乃尋求簡單的計算方法。當時在蘇格蘭恰好出了一本書

"Mirifici logarithmorum Canonis descriptio, seu ... , auctore ac inventore Joanne Nepero barone Merchistonii"
（驚動人的對數規則與記述，即……著者兼發明者 John Napier, Merchistonii）

這是1614年的事，傳說著者 Napier 在1550年出生於蘇格蘭的一小市鎮，Napier 原先是長老教會的修道士，他認為對人類最大的奉獻是傳授其教義之精神。這個非數學家的 Napier，為什麼著手研究發明對數呢？詳情不得而知，或許他常聽到有人為龐大的數值計算而感到苦惱，尤其是商、積之計算，因此引起了他推敲是否有簡單的計算方法。大概因之而發現他的對數法則吧！

Napier 首先所推考的是將大數的積或商的近似值計算，轉變成和或差的演算。於是由積與和的對應，注意到等比級數與等差級數的對應，但怎樣的等比級數對應怎樣的等差級數乃是個問題，這就是在 Napier 的創意中的關鍵。

Napier 最先考慮沿直線運動的兩點 P,Q。P 是在定長 AZ 之始點 A 到終點 Z 的運動。點 Q 則無限制地從直線 A'Z' 之始點 A' 點向 Z' 方向做運動，P,Q 以同速出發。點 Q 以等速運動，點 P 之速度由此點到 Z 的距離來決定，做減速運動。如點 P 在 B 點時，Q 在 B'，此時就稱

A'B' 為 AB 的對數。

這就是「Napier 對數」的基本定義。僅就此定義，則尚無法出現「Napier 對數」的性質。為示明其性質，乃取 AZ 長為 r，r 可以為很大的值。在點 A 的 P 之速度為 r。P,Q 從 A,A' 出發，經過時間 $\frac{1}{r}$ 時，P,Q 分別抵達 B,B'。當 r 非常大時， $\frac{1}{r}$ 等於瞬間的短時間。此時 P 到 B 的距離等於 r x (1/r)=1，Q 到 B' 的距離也等於 1。今 P 在點 B 的速度等於 BZ 的長，即

$\begin{displaymath}BZ=r-1=r(1-\frac{1}{r})\end{displaymath}$

故在時間 $\frac{1}{r}$ 內，點 P 到達 C，點 Q 到達 C'，則

$\begin{displaymath}BC= \frac{1}{r} \cdot r(1- \frac{1}{r})=1- \frac{1}{r}, \quad B'C'= \frac{1}{r}\cdot r=1\end{displaymath}$

於是

$\begin{displaymath}CZ=AZ-AB-BC=r(1-\frac{1}{r})^2 \end{displaymath}$

又再經 $\frac{1}{r}$ 時間 Q 到 D' 點，則 C'D'=1，而點 P 在 C 點的速度是 $r(1-\frac{1}{r})^2$ ，故 P 在 $\frac{1}{r}$ 時間內的距離為 $CD = (\frac{1}{r}) \cdot r(1-\frac{1}{r})^2$ $= (1-\frac{1}{r})^2$ ，因此

$\begin{displaymath}DZ=AZ-AB-BC-CD=r(1-\frac{1}{r})^3\end{displaymath}$

循此下去，可知點 P 在 A,B,C,D, $\cdots \cdots$ 各點的速度分別為

$\begin{displaymath} r, \; r(1-\frac{1}{r}), \; r(1-\frac{1}{r})^2, \; r(1-\frac{1}{r})^3, \; \cdots \cdots \end{displaymath}$

(1)

其所對應的 Q 點位置 A',B',C',D', $\cdots \cdots$ 為

$\begin{displaymath} 0,\quad 1, \quad 2,\quad 3, \cdots \cdots \end{displaymath}$

(2)

（注意(2)之數 n 與(1)中出現之 $(1-\frac{1}{r})^n$ 的次數 n 相同。） (2)式的每一個值，依定義是(1)式所對應之「Napier 對數」。

為瞭解「Napier 對數」的性質，茲用現代的數學形式來說明。設

$\begin{displaymath} x=r(1-\frac{1}{r})^y \end{displaymath}$

(3)

y 就是「x 的 Napier 對數」，此 Napier 對數以

$\begin{displaymath} \mbox{Nap.} \log{x} = y \end{displaymath}$

表示，這並不是 Napier 所用的記號。

依自然對數的性質，由(3)可導出

$\begin{displaymath}\log_e x = \log_e r +y \log_e { (1- \frac{1}{r}) } \end{displaymath}$

於是

$\begin{displaymath}y = \frac {\log_e{x}-log_e{r}}{ \log_e(1- \frac{1}{r})} = \frac {r( \log_e{r}-log_e{x})} {-r \log_e {(1-\frac{1}{r})}}\end{displaymath}$

但

$\begin{displaymath}-r \log_e {(1-\frac{1}{r})} = 1 + \frac{1}{2} \cdot \frac{1}{r} + \frac{1}{3} \cdot \frac{1}{r^2} + \cdots \cdots \end{displaymath}$

故

$\begin{displaymath}y = \frac{ r(\log_e{r}-\log_e{x}) } {1+ \frac{1}{2} \cdot \frac{1}{r} + \frac{1}{3} \cdot \frac{1}{r^2}+ \cdots \cdots}\end{displaymath}$

若令 r 為極大的值，則上式之近似值成為

$\begin{displaymath}y = r(\log_e{r}-log_e{x})\end{displaymath}$

故得

$\begin{displaymath} \mbox{Nap.} \log x = r(\log_e{r} - \log_e{x}). \end{displaymath}$

(4)

這樣一來

$\begin{displaymath} \mbox{Nap.} \log r = 0 \end{displaymath}$

(5)

這就是 Napier 對數的特性，易於看出「x 大於 r 時， $\mbox{Nap.} \log x$ 為負值，x 小於 r 時， $\mbox{Nap.} \log x$ 為正值」。

其次設

$\begin{displaymath} x = r(1- \frac{1}{r} )^y , \quad x'=r(1- \frac{1}{r} )^{y'} \end{displaymath}$

則

$\begin{displaymath}xx'=r^2(1- \frac{1}{r})^{y+y'}.\end{displaymath}$

於是得

$\begin{displaymath} \frac{xx'}{r}=r(1-\frac{1}{r})^{y+y'} . \end{displaymath}$

依「Napier 對數」的定義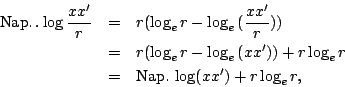

$\begin{displaymath} \mbox{Nap.} \log {\frac{xx'}{r}}=y+y'= \mbox{Nap.} \log x + \mbox{Nap.} \log x'. \eqno{(*)} \end{displaymath}$

由(4)得

$\begin{eqnarray*} \mbox{Nap.} . \log {\frac{xx'}{r}} & = & r(\log_e{r} -\log_e{... ...{(xx')})+r \log_e r \\ &=& \mbox{Nap.} \log(xx')+r \log_e r , \end{eqnarray*}$

於是將 $\mbox{Nap.} \log(\frac{xx'}{r})$ 代入(*)得

$\begin{displaymath} \mbox{Nap.} \log{(xx')}=\mbox{Nap.} \log x + \mbox{Nap.} \log{x'}-r\log_e{r}. \end{displaymath}$

(6)

又

$\begin{displaymath}\frac{x}{x'}=(1-\frac{1}{r})^{y-y'}, \end{displaymath}$

故

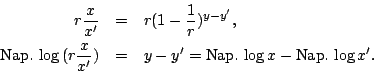
$\begin{eqnarray*} r \frac{x}{x'} &=& r(1-\frac{1}{r})^{y-y'}, \\ \mbox{Nap.} ... ...{x}{x'})} &=& y-y'= \mbox{Nap.} \log x - \mbox{Nap.} \log{x'}. \end{eqnarray*}$

依(6)所示之性質

$\begin{displaymath} \mbox{Nap.} \log{(r \frac{x}{x'})} = \mbox{Nap.} \log r + \mbox{Nap.} \log{\frac{x}{x'}}-r\log_e r \end{displaymath}$

在(5)所示， $\mbox{Nap.} \log r$ 為 0，故

$\begin{displaymath} \mbox{Nap.} \log{(r \frac{x}{x'})} = \mbox{Nap.} \log{\frac{x}{x'}}-r\log_e r \end{displaymath}$

結果得

$\begin{displaymath} \mbox{Nap.} \log{\frac{x}{x'}}= \mbox{Nap.} \log x -\mbox{Nap.} \log{x'}+r\log_e r \end{displaymath}$

(7)

從(6)與(7)所示的性質來看，「Napier 的對數」對於自然對數或常用對數之積、商的計算，本質上是具有同樣之性質。Napier 是以三角函數之計算為對象，因此取 r=1000000 時，決定 $\mbox{Nap.} \log{\sec{90^{ \circ }}}=0$ 。（參照(5)式）在那個時代既無 10⁷ 之記法，又欠小數之知識，所以才用那麼大的數吧！

Napier 死後出版有《De arte logistica》（計算技術的方法）。Napier 對於代數或幾何所寫的雜錄，不問其完成與否，據說有遺稿集，然因未目睹其中內容，故未能多言，但由「logistica 意指做好計算」來看，Napier 的數學所示之一面是以計算為主的學問。

參考資料：
: Sugaki seminar special number, 1971年12月。

對外搜尋關鍵字：
．對數
．Napier
．Kepler

編者按

三角學源起於天文。（見圖）起初大家有興趣的是求一大圓中角 2θ 所對的弦長 BC（記做 $\mbox{cd} 2 \theta = BC$ ），後來又演變成求相應於角 θ 的 BD（即 $\sin{\theta} = BD$ ）。 $\sin$ 函數和 $\mbox{cd}$ 函數有密切的關係： $\sin{\theta}=\frac{1}{2} \mbox{cd} 2 \theta$ 。這就是「正弦」函數名稱的由來。最可注意的是那時 $\sin$ 函數的值是線段長而不是我們現在所知的比值。這樣的 $\sin$ 值當然和圓半徑的大小有關。最早的時候習慣取定半徑的長度為 60 個單位（若用 3 做圓周率，則圓周要有 360 個單位長，所以每一度所對的弧長為一個單位），而製造三角函數表。當然大家知道這樣的函數表是要相對於半徑長來看才會真正有用。（實際上這就是現代的三角函數的觀念。）如果要得到較精確的函數值，則其小數部分不能隨便捨去；但那時候的歐洲人不懂得小數表示法，他們只會用分數，而且分數的符號及運算技巧都非常笨拙。為了避免計算上的困難只有將半徑的單位個數加大，使得相應函數值小數以下的部分可以略去。在 Napier 的時侯，通常三角函數表中的半徑長變成 10⁷ 那麼大，於是當他為了解決天文上計算的困難而做對數表時，他就取 r 長為 10⁷。在這樣的 r 長之下， $\sin{90}^{\circ}=10^7$ 所以 $\mbox{Nap.} \log \sin 90^{\circ}=0$ 。

Napier 的對數（其底數為 $1-\frac{1}{10^7}$ ）是由三角學的計算而起的，不好用到其他方面的計算。他及 Henry Briggs（1561～1631）不久就發現以10為底的對數最方便最實用，所以 Napier 的對數只曇花一現，不久就被常用對數替代了。


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：康明軒 ∕ 校對：鄧惠文 ∕ 繪圖：張琇惠

最後修改日期：4/26/2002