現代統計學的發展

「統計」這個名詞的意義因人而異，對一般人而言，統計是任何方面專家們用以支持其論點的一大堆數字；對於略具常識的人來講，這個名詞代表用以摘要和解釋一堆數據如計算平均數 (mean) 與標準差 (Standard deviation) 的程序之類的概念。但是對於從事統計工作的人員而言，統計是依小量數據（樣本）所提供的資料以估計預測某研究對象如群體的方法。或者更廣義地說，統計為面對不定狀況制定決策提供方法的科學。

雖然統計的起源可追溯至十八世紀甚至更早，然而統計學主要的發展卻遲至十九世紀末葉二十世紀初期才真正開始。到了四十年代才逐漸成熟，統計學和機率論的關係異常密切，事實上任何統計問題的研究都必須牽涉到機率論的運用，因為後者實為前者的主要工具。

統計人員對如下所舉之類問題的答案深感興趣：是否接受本批送驗成品？吸煙與得癌症有關嗎？張三會於下屆選舉中獲勝嗎？為了回答上述問題，我們必須由具「代表性」的特殊狀況以「瞭解」一般的狀況，由樣本「推測」群體。因此，由統計人員所推測得到的結論都不是絕對肯定可以接受。事實上，統計人員的職責之一是量度他所得結論肯定的程度，但是我們不能以為統計的缺乏肯定性而誤認為統計數學不嚴密，因為構成統計基礎的數學是機率論，它有固若磐石的數理化基礎和經嚴密證明的定理。

一般而言，我們可以把統計問題分成兩類：敘述統計和推論統計，簡單的說：任何對數據（即樣本）的處理導致預測或推論群體的統計稱為推論統計。反之，如果我們的興趣只限於手頭現有的數據，而不準備把結果用來推論群體則稱為敘述統計。舉個例子來說，依據過去十年來的統計，每年來華觀光的人數，平均每人在臺停留的日數，平均每人每天在華的花費，十年內那一年創最高記錄等等都是屬於敘述統計的範圍；但是如果我們根據這些年所得的數據來預測來年可能的觀光客人數就是推論統計的問題了。十年前的初級統計課本大多談敘述統計，如今由於計算機的盛行，這部份的工作大多利用計算機來解決，稱為數據處理，而一般統計書的重點別放在推論統計。

大致說來，推論統計分為三大類，就是估計，檢定和分類與選擇。譬如說，張三想競選臺北市議員，他想估計一下可能有多少人會投票給他，於是他以隨機抽樣的方式，詢問100位有投票權的市民的意見，而後根據所得結果推論可能全市有多少人會選他，這是估計問題。又如某家庭主婦想知道她心中懷疑潔王牌洗衣粉的洗淨力是否比愛王牌洗衣粉強，首先假設潔王牌比愛王牌好，然後經過試驗來測定這假說是否成立，在本例中，我們並不想估計任何參數，而只是想檢驗事先所敘述的假設是否成立其可靠性有多大，這就是檢定問題。還有，新製造的三種藥品中那幾種比目前所用的這種藥品有效呢？這是選擇的問題。如果我們把統計設想為經由抽樣以制定決策的科學，那麼我們似乎宜以十九世紀末期高爾頓爵士（Sir Francis Galton, 1822～1911）和卡爾．皮爾遜（Karl Pearson, 1857～1936）的論述做為它的起點。從那時開始，現代統計理論的發展可略分為四大思潮，在這四大時期，每一階段都是以一位偉大的統計學家的專著為先導 ^註1。

第一階段隨著1899年高爾頓的《Nature Inheritance》一書的出版而展開序幕，該書除了其本身的價值外，還引發了傑出的統計學家卡爾．皮爾遜對統計學的興趣。在此之前，皮氏只是在倫敦大學的大學部 (University College) 執教的數學教員。當時，這「所有知識都基於統計基礎」的想法引起了他的注意。

1890年他轉到格里辛學院 (Gresham College)，在那裏他可講授任何他希望講授的課程，皮氏選了一個題目「現代科學的範圍與概念」(the Scope and Concepts of modern Science) 在他的授課中他越來越強調科學定律的統計基礎，後來他全神集中致力於統計理論的研究。不久他的實驗室成為世界各地人們學習統計和回國點燃「統計之火」的研究中心。經由他熱心的提倡，科學工作者逐漸由對統計研究不感興趣的境地轉而成為熱切地努力發展新理論和搜集並研究得自各方面的數據。人們越來越深信統計數據的分析能為許多重要的問題提供解答。

海倫．華克 (Helen Walker) 描述皮氏小時候的一則軼事，生動地顯示他往後事業中所表現的特色 ^註2 。有人問皮爾遜他所記得最早的事，他說「我不記得那時是幾歲，但是我記得是坐在高椅子上吸吮著大拇指，有人告訴我最好停止吮它，不然被吮的大拇指會變小。我把兩手的大拇指並排看了很久，它們似乎是一樣的，我對自己說：我看不出被吸吮的大拇指比另一個小，我懷疑她是否在騙我」。

在這個單純的故事中，海倫華克指出「不盲信權威，要求實證，對於自己對觀測數據的意義的解繹深具信心，和懷疑與他的判斷不同的人態度是否公平」這些就是皮氏一生獨具的特徵。

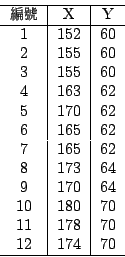
$\begin{displaymath} \begin{tabular}{c\vert c\vert c} \hline \mbox{{\fontfamily{c... ...4\\ 10&180&70\\ 11&178&70\\ 12&174&70\\ \hline \end{tabular}\end{displaymath}$

這個第一階段的特點就是人們對統計的態度轉變了，統計的重要性被科學界所承認。除此之外，在統計技巧上也有很多的進展，我們利用上面這個十二個人的身高和體重的數值表介紹一些最基本的統計觀念，其中身高 X 以公分為單位，體重 Y 以公斤為單位。

為了對這組資料得到一點概念，我們把它列成圖形。英人普萊菲（William Playfair, 1759～1823）被公認為將圖形表示的概念介紹到統計學的第一人。他的著作，大多為關於經濟學，多採用圖形如直方圖、條形圖。在我們上述問題中，用次數圖就能很清楚地表示出來，圖一就是身高 X 的次數圖，體重 Y 的次數圖也很容易表示。有興趣的讀者不妨一試。雖然這類圖形能幫助我們的直覺，但是如果想對這些數據更一步瞭解，我們必得進一步用某些量來描述它們。在這類數量中最重要之一是對於集中趨勢的測度。最早的集中趨勢的測度實際上可追溯至古希臘，是算術平均數 $\mu_x$ ，即

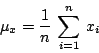
$\begin{displaymath} \mu_{x}=\frac{1}{n} \, \sum^n_{i=1}\,x_i \end{displaymath}$

$\begin{displaymath} \mu_x=\frac{1}{n} \, \sum x_j f_j \end{displaymath}$

假設有一根無重的木桿，其上刻著變數 Y 的各不同值的刻度，並且設想在 x_j 處掛著質量 $\frac{1}{n}\,f_j$ 的物品，則整個體系的質量為 1，而 $\mu_x$ 為質量重心，也就是說如果把支點設於 $\mu_x$ ，則整個體系會趨於平衡，以本例的身高而言，其體系如圖二所示。

這種對平均數的解釋在以後我們思考連續分配觀念時，很有幫助。

雖然中位數 (median) 觀念可能早已有之，但是遲至1883年才經由高爾頓把它引入統計，成為集中趨勢第二種測度 ^註3 。所謂中位數就是所有觀測值依大小排起來，中間的那個數，若是偶數個數就是兩個中間數的平均數，在我們例子中身高的中位數為165。

另外還有一個集中趨勢的測度是眾數，1894年左右由卡爾．皮爾遜所介紹。眾數如果存在的話，就是出現次數最頻繁的數值，如果兩個或兩個以上的數值出現次數相同，眾數就不太有意義了，在我們例子中體重的眾數是62。

如果變數 X 的分配是完全對稱，即其次數圖完全地對稱於一垂直線，那麼平均數、中位數和眾數（如有一眾數存在的話）會重合為一點。讀者們應注意，反過來說並不成立。也就是說不對稱的圖形也可有平均數，中位數和眾數重合的情形（即平均數、中位數和眾數重合並不保證圖形為對稱）。

對大多數的目的而言算術平均數是最常用的集中趨勢測度，這當然有它學理上的意義。雖然有時候計算相當費時，中位數也有它的優點，它不受少數極端值的影響。例如在我們的例題中，若把一個身高180公分的人換成一個200公分的人，平均數就會受到很大的影響，而中位數卻全然不變。

其次我們談一下「離差」(dispersion) 的測度，它是數據以平均數為準對於分散程度的測度。最早這種測度大概是貝塞（Bessel）於1815年用於有關天文學問題的「可能誤差」。目前最通用的是「標準差」σ，這個名詞是1894年卡爾．皮爾遜所創。

$\begin{displaymath} \sigma_x = \big[\frac{1}{n} \sum^n_{i=1}(x_i-\mu_x)^2 \big]^{1/2} \end{displaymath}$

為了介紹相關的觀念，我們回頭再仔細看一下表一中的身高和體重，數值顯示這兩個變數似乎有某種相關存在，根據常識，高的人通常要比矮的人重，在這些數據點繪在直角坐標的平面上，可以看出它們之間的關係，稱為分佈圖（參見圖三）

如果它們之間為線性關係，則點的趨向會呈現在直線的附近。

在十九世紀末葉，有人問高爾頓爵士這種兩組數據之間的關係是否可以測度？他想出了相關的觀念。但是我們現在所用的相關係數ρ 卻是卡爾皮爾遜所創，其定義為

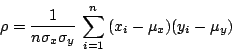
$\begin{displaymath} \rho=\frac{1}{n \sigma_x \sigma_y}\,\sum^n_{i=1}\,(x_i-\mu_x)(y_i-\mu_y) \end{displaymath}$

經由簡單的代數運算，我們可以證出ρ的數值介於 -1 與 +1 之間，0 值表示沒有直線關係存在， $\pm 1$ 表示數據應在正斜率的直線上，-1 表示數據在負斜率的直線上，在 $\pm 1$ 附近的相關係數表示兩變數有相當高的直線關係，接近 0 的相關係數表示兩變數沒有直線關係，在我們的例子中，ρ 大約為 0.9。注意ρ是直線關係的測度，數據可能形成一團，這時 $\vert\rho\vert$ 值會很小，然而它們雖不是直線相關，但卻無疑是相關的。

高爾頓是著名的演化論者達爾文的表親，曾為達爾文做過一些統計工作。我們在上節曾提到他對相關概念的研究，但是教師們最不會忘記的高氏的貢獻是他首創把成績評分與常態曲線拉上關係。

常態曲線至少可追溯至1733年的棣美弗（Abraham De Moivre）的導證，是一個統計上非常有用的觀念。它的方程式為

$\begin{displaymath} f(x)=\frac{1}{\sqrt{2\pi}\sigma}\mbox{exp}[-\frac{(x-\mu)^2}{2\sigma^2}] \end{displaymath}$

常態分配的優點是不論其平均數 μ 和標準差（ $\sigma >0$ ）之值為何，均可經過標準化 $z=\frac{x-\mu}{\sigma}$ 的變換，轉換成平均數為 0 和標準差為 1 的標準常態分配。如果把在常態曲線下由 $-\infty$ 到 $+\infty$ 的面積積分的話，結果是 1。大約有三分之二的面積在以平均數為中心左右一個標準差之間。在任意區間 $a \leq x \leq b$ 之間常態變數的機率的求法就是等於求在這區間之上，常態曲線之下所圍成的面積，這種數值可由任何標準的數表中查出。

早先在談離散分配的時候，我們曾經提到算術平均數可以看成是總質重等於 1 的離散質點體系的質量重心。剛才我們提到的常態曲線是一個連續分配的例子，依據類比的方式，我們可以把常態分配與一根理想化向兩端無限伸長質重為 1 而其密度則為依決定常態分配的函數 f 而變動分佈的棒相聯接。依據微積分，這種桿棒的質量中心是

$\begin{displaymath} \mu =\int^{\infty}_{-\infty} \, x f(x) \,dx \end{displaymath}$

$\begin{displaymath} g(x)=[\pi(1+x^2)]^{-1} \end{displaymath}$

同理，依據離散變數的標準差公式，我們可以定義出連續分配的標準差為

$\begin{displaymath} \sigma =[\int^{\infty}_{-\infty}(x-\mu)^2 f(x)dx]^{1/2} \end{displaymath}$

費雪還有很多其他的貢獻，早先我們曾提到他介紹了一樣本統計量是否為一個群體參數的好估計量的判定準則，包括了一致性，效率性和充足性等概念就是在1921年一篇重要文獻中提到的。在這類文章中，他還曾介紹最概估計量 (maximum likelihood estimation) 的觀念。

1919年費氏離開他在中學教數學的工作，轉至羅森斯得農業試驗站 (Rothamsted Agricultural Experimental station)，在這裏他發展出現在世界通用的抽樣技巧和隨機程序。他的兩本名著《Statistical Methods for Research Workers》和《Design of Experiments》分別於1925年和1935年出版，對於統計有重大的影響。後者的第二章曾列入《數學世界》 ^註5，在這篇非常引人入勝的文章中，費氏提到有一位女士聲稱她能分辨出她的茶中牛奶是在泡茶之前或之後加入的，而後他描述一種實驗計劃來證明或否定該女士的聲稱。

為了想答覆關於群體的問題，由實用的觀點來看，我們必須由群體中選取樣本，然後依據樣本所提供的資訊推論母體。母體所涉及的如母體均值 μ 和標準差 σ 都是未知，假設有一個樣本被很適當地選出（如何選法是一個很重要的統計問題），依據樣本可以得出相當好的母體參數或某量的估計值。早先我們曾提到費雪提出母體參數的好樣本統計量的判別準則，我們只是很簡要的提出，假若 (x₁, $\cdots\cdots$ ,x_n) 代表一組由母體均值為 μ、標準差為 σ 的群體中選取的樣本，則分別定義如下的樣本平均數 $\overline{X}$ 和樣本標準差 S。

$\begin{displaymath} \overline{X}=\frac{1}{n} \sum^n_{i=1} x_i \quad \mbox{{\font... ... \big[ \frac{1}{n}\sum^n_{i=1}(x_i-\overline{X})^2 \big]^{1/2} \end{displaymath}$

如果我們由一個群體取出很多組樣本，並且每組均計算 $\overline{X}$ 值，我們就可得到很多不同的數值，而這些數值會趨於接近群體平均數 μ。這樣看來， $\overline{X}$ 也是一個變數呈某種形式分佈，這就引起了一個重要問題：若已知群體變數為某種分配，則樣本平均數又如何分配？下述定理，我們僅敘述而不證明，可回答部份這個問題。

回想標準差的重要性，我們的結論是當樣本大小越大，則 $\overline{X}$ 值接近 μ 的機率也愈大，如圖五所示。在應用這個定理時，受到一個嚴格的限制，因為實際上的任何群體是否確實為常態分配很可懷疑。有很多群體變數甚至不近似常態分配，但有一個在機率論上最著名的定理，也是在所有數學中最著名的定理之一可以部分幫助解決這個問題是中央極限定理，其中一種形式敘述如下：

中央極限定理有一段相當長的發展史，1773年棣美弗證明其第一種形式即考慮擲硬幣只有兩種可能出現的情形，我們在前面所說的形式是1922年凌德柏 (J.W.Lindeberg) 所述 ^註7 。近來俄國數學家甚至給出 $\overline{X}$ 以常態分配為其極限分配的充要條件，把本定理推廣至其極致。為了顯示統計學家對中央極限定理的用法，我們來看由霍爾 (Paul G. Hoel) 編著的統計教本 ^註8 中的一個典型問題「某細繩製油商由過去的經驗發覺某種細繩的平均耐拉力為15.6磅，標準差為2.2，現試將這種細繩的製造過程時間縮短，而後取50條細繩為樣本做試驗。結果發現其平均耐拉力減為14.5磅，試問依據這個樣本，是否應下結論為「新製造程序對繩子拉力有壞的影響?」」

統計人員稱這種問題為假說檢定，我們必須檢定假說 $H_0:\mu=15.6$ 對 $H_1:\mu <15.6$ ，雖然製造程序改變，標準差也很可能改變，但是我們仍假設耐拉力 X 的標準差為2.2磅，現在我們用到了中央極限定理，不論 X 如何分配， $\overline{X}$ 為平均數 μ 和標準差 $\frac{\sigma}{\sqrt{n}}$ 的近似常態分配，或者說 $z=(\overline{X}-\mu)/\sigma$ 為平均數 0 和標準差 1 的標準常態分配。然後我們查數值表，發現 $\overline{X}=14.5$ 遠離15.6，如果假說 H₀ 成立的話， $\overline{X}=14.5$ 的機率僅0.0002，因此我們棄卻 H₀ 而接受 H₁。依照通常在 H₀ 成立的假說下， $\overline{X}$ 值出現的機率僅0.05時即棄卻 H₀ 的原則，由數表可知當 $\overline{X}$ 小於15.09，我們就應判定棄卻 H₀，任意小於15.09的數值稱為在臨界區域。

我們再回頭提一下假設新製程的標準差 σ 不變的誤差機率。事實上，這時 σ 已不是一個已知數，但是我們可以計算出樣本標準差 S，在1908年化學家高塞特（William Gosset）以 Student 的筆名發表他發現的統計量 $t=(x-\mu)\sqrt{n-1}/s$ （注意 σ 被 S 取代）的分配，他指出若 X 為常態分配，則 t 為自由度 n-1 的 student t 分配，這種分配相當重要，其分配數值在一般統計數表中均有列出。雖然高塞特於1908年發現 t 分配，但是他的結果只是一種猜測，直到1926年才由費雪加以嚴密的證明。在此 X 為常態分配這條件非常緊要，但是即使 X 僅為近似常態分配，統計學家發現當 σ 為未知，尤其是當樣本數 n 值很小時，非常適宜採用 t 分配。當 n 相當大時，S 和 σ 的差別越來越小，因此不太需要使用 t 分配數值表。

第三個時期以為在1928年聶曼（Jerzy Neyman）和伊根．皮爾遜（Egon Pearson, 卡爾．皮爾遜之子）的共同論文多篇的發表為開端，這些論文介紹和強調諸如驗定問題中的第二種錯誤，檢驗的檢定力和信賴區間之類的觀念。在這期間，工業界開始大量採用統計技巧，尤其是與品質管制有關的統計。並且由於人們對調查工作的感興趣導向對抽樣理論與技巧的研究，1928年聶曼和伊根．皮爾遜的論文為檢定與估計理論帶來一種嶄新的面貌。包括對許多費雪早先提出的想法的重新加以整理和修正，例如在細繩製造商的問題中，我們早先得到的結論是：若一樣本的樣本平均數值小於15.09則棄卻假說 H₀。聶曼和皮爾遜提出如下之類的問題：為什麼我們要設15.09以左為臨界域？為什麼不取0.025在分配曲線極左的面積和0.25在分配曲線極右的面積成「雙尾」(two tailed) 臨界區域？

於選取臨界域時必須採何種準則？我們必須要用直覺還是用嚴謹的數學？我們得到如圖八的結論牽涉到兩種不同型態的錯誤，聶曼和皮爾遜命名為第一種錯誤和第二種錯誤。聶曼和皮爾遜總結他們的發現歸納成為下述原則：在所有具有相同第一種錯誤的試驗（臨界域）中，我們選用具最小第二種錯誤的臨界域。

	H₀為真	H₁為真
$\overline{x}\geq 15.09$ 接受H₀	正確決定	第二種錯誤
$\overline{x} < 15.09$ 接受H₁	第一種錯誤	正確決定

雖然本原則的應用相當複雜，聶曼和皮爾遜的影響使本原則及其相關的檢定力函數成為重要的統計概念，並且發展出討論這類問題的一般數學理論。

談現代統計學的發展，實不能不提華德（Abraham Wald, 1902～1950） ^註9 ，否則必定顯得不完備。華德的第一篇論文關於目前常見的統計程序──逐次抽樣 (sequential sampling) 的出現第四時期的開始。這篇1939年的論文是華德一連串論文的起始，不幸正當他的創新力處於顛峰時卻由於飛機失事死於非命。華德最大的貢獻之一是他介紹一種對統計問題的新看法(1945)，那就是以對局的觀點去處理統計方面的問題，這就是今日所稱的統計決策理論 (statistical dicision theory)。從這個觀點，統計被視為以自然為對手的對局的藝術，這是一個相當廣義的理論，雖然它牽涉到相當複雜的數學，但是平心而論，我們可以說大部分目前的統計研究人員發現採用這種新觀點非常理想。華德對統計理論發展的方向有重大的影響，他的「門徒」們多成為今日統計界的領袖人物。

華德誕生在羅馬尼亞，是正統的 (orthodox) 猶太世家，由於它的宗教信仰，使他受教育的機會受到某些限制，而必須靠自修彌補。他自修的結果竟能對希爾伯特 (Hilbert) 的《Foundation of Geometry》提出有價值的見解，他的建議列入該書的第七版中，這一事實充分顯示了他的數學天賦。後來華德進入維也納大學並且在僅修了三門課之後就得到博士學位。在這個時期的奧地利，由於政治上的因素使他無法從事學術工作，只好接受一個私人職位，職責是幫助一位銀行家增廣高等數學知識，他因此對經濟學深感興趣，後來成為經濟學家摩根斯坦 (Oskar Morgenstern) 的親信助理。摩氏曾與馮紐曼 (John Von Neumann) 共同合作從事研究並奠定了對局論 (game theory) 的基礎。

華德在二次大戰前到達美國，他的父母和姊妹不幸沒有逃出來，結果死於納粹的瓦斯房。華德由於對經濟學的興趣接觸到統計學，逐漸轉向從事統計學的研究，不久竟成為一位傑出的理論統計學家。除了統計決策理論之外，華德對統計還有很多重要的貢獻，在此我們提出主要的一個，就是逐次分析。雖然這個理論可能不是他所首創，但卻是他發展完成的(1943)。這個技巧在減少生產製程中的抽樣數方面非常重要，二次大戰期間曾被列為機密。

現在我們以工業方面的品質管制問題為例來說明逐次分析的觀念，在逐次方法未發表之前，標準的抽樣程序是由製成品中抽取定量的樣本，然後依據樣本中所含不良品數的多寡判定允收或拒收該批。這種程序忽略了關於製成品批的優劣資訊可由在抽樣過程中不良品出現率的大小獲得的事實。

在逐次抽樣中，我們把抽樣過程中可能發生的狀況分為三類：

這三個區域的劃分準則視所允許的第一種錯誤和第二種錯誤而定。在本例中，在查驗第六十個製成品後才判定允收。

由圖形中可見，這種抽樣方法可能很快就能決定是否允收，也可能在中間區域停留很久的時間，但是華德證明允收或拒收的決定能於有限步內達成的機率為1，實際經驗顯示逐次抽樣和傳統的固定樣本大小的程序相比在抽樣費用方面約可節省一半。

除了上述四大統計思潮外，1933年俄國數學家柯摩哥羅夫 (Kolmogorov) 發表《Foundation of the theory of probability》為統計學理論奠定了邏輯基礎。在統計應用技巧方面，電子計算機的發展和使用是一大革命。十九世紀末葉開始，美國人口調查局 (U.S. Census Bureau) 每十年舉辦一次人口普查，後來，由於人口的漸增，人口調查局發現他們已越來越無法處理所蒐集的成堆數據。賀爾瑞茲 (Herman Hollerith) 想出許多利用打孔卡片 (punched card) 記錄數據的方法，並且發明機械能讀這些數據和處置資訊 (Information)，在賀氏的指導下，1894年人口調查局的工作利用打孔卡和讀卡機，提高不少效率。雖然1890年人口調查時，美國人口比1880年增多了約百分之二十五，但是工作完成所費的時間卻僅為其三分之一。

電子計算機於二次大戰後發展一日千里，1950年後漸進入實用階段。計算機的出現不但使統計計算工作簡化，而且快捷。尤其是有了統計成套程式 (Statistical package) 以後，更為方便，只要知道應採用何種統計方法就能使用。1972年惠普 (Heweleit Packard) 公司發展出掌上型計算器 (calculator)，對於一般小統計問題的解決，更是方便，不必因為統計問題特地到計算機中心去。

統計為一科學方法，其可應用範圍，遍及自然科學及社會科學的整個領域中的許多部分，大凡農業、工業、商業、教育、醫藥、政治、社會、經濟等等許多問題無不適合採用統計方法處理，統計學傳入我國雖已有相當時日，但是我國目前還只有政府機關較為重視，民間工商企業近年來雖然也漸漸講求科學管理，但是大多未能應用統計方法。

: 1. Dale E.Varbery 《The development of modern statistics》 Part I, II, The Mathematics Teacher April 1963 p.252-257 May 1963 p.44-348.
: 2. Mario F.Triola 《Mathematics and the modern world》 Cummings Publishing Company, 1973.


	（若有指正、疑問……，可以在此留言或寫信給我們。）