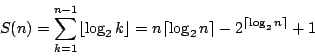整理與合併問題

．原載於數學傳播第二卷第四期
．作者當時任職於美國貝爾實驗室

整理與合併問題

黃光明

假設有 n 個物品，重量互異，我們要把這些物品按照其重量大小整理起來。我們所有的工具是一個有兩個托盤的天平，兩端放上東西後，天平可以指出孰重孰輕。現在假設每一次秤時，每個托盤中祇能放一樣東西，問最少需秤多少次才能「保證」整理完成。這是「整理」(sorting) 問題。

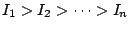令 I₁,I₂,…,I_n 代表這 n 個物品，當運氣好時我們可能在第一次秤時，發現 I₁ 比 I₂ 重，第二次秤時，發現 I₂ 比 I₃ 重，……，第 n-1 次秤時，發現 I_n-1 比 I_n 重。則一共祇用了 n-1 次，就可把 n 個物品整好，即 $I_1>I_2>\cdots>I_n$ ，但運氣不這麼好時，很顯然 n-1 次就不夠了。我們關心的，是在運氣最壞時，你提出的方法需要秤多少次。換句話說，不管運氣如何，你的方法必需保證秤這麼多次後，一定可以整理完畢。我們現在以這個「保證數」來比較不同的方法，而要選一個保證數最小者，稱為最佳法。

假如有兩堆個數分別為 m 和 n 的物品，已分別整理好。現在要把這兩堆物品合併成一堆（仍需整理好），問最少需再秤多少次，才能保證合併完成。這是兩個集合的「合併」(merging) 問題。合併問題可以推廣到 s 個集合，不過本文祇牽涉了兩個集合的情形。

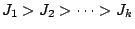Steinhaus（參考 9）首先提出整理問題。他建議一個遞歸 (recursive) 法來整理 n 個物品。即先整理好 I₁,I₂,…,I_k+1，再把 I_k+1 合併進去，使 I₁,I₂,…,I_k+1 都整理好。如此從 k=1 一直到 k=n-1 遞歸進行，在最後一次把 I_n 合併入已整理好的 I₁,I₂,…,I_n-1 後，即完成了 n 個物品的整理。令 $J_1>J_2>\cdots>J_k$ 為已整理 {I₁,I₂,…,I_k}，則 I_k+1 合併入 {J₁,J₂,…,J_k} 用的是中分法 (binary insertion)，即把 I_k+1 和 {J₁,J₂,…,J_k} 中重量居中的一個物品（如有二物品居中，任擇其一）放上天平兩端比較。假設 J_h 是拿來和 I_k+1 比較的物品。當 I_k+1 比 J_h 重時，下一次即從 {J₁,J₂,…,J_k-1} 中選出一重量居中的物品和 I_k+1 比較，當 I_k+1 比 J_h 輕時，下一次即從 {J_h+1,J_h+2,…,J_k} 中選出一重量居中的物品和 I_k+1 比較，如此重複進行，一直到 I_k+1，在 {J₁,J₂,…,J_k} 中的位置完全確定，即 {I₁,I₂,…,I_k+1}已整理好成{J₁, J₂,…,J_k+1} 時始畢。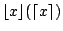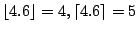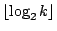定義 $\lfloor x \rfloor (\lceil x \rceil)$ 為不超過（不低於）x 值的整數中最大（小）的一個（如 $\lfloor4.6\rfloor =4,\lceil4.6\rceil=5$ ）則把 I_k+1 合併入 {J₁,J₂,…,J_k} 至多需比較 $\lfloor \log_2{k} \rfloor$ 次，所以 Steinhaus 的遞歸法可以在

$\begin{displaymath} S(n)=\sum_{k=1}^{n-1} \lfloor\log_2{k}\rfloor =n \lceil \log_2{n} \rceil-2^{\lceil\log_2{n}\rceil}+1 \end{displaymath}$

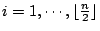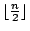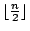次數內保證完成整理（參考3）。 Ford 和 Johnson（以下簡稱 FJ）提出一不同的遞歸法。此法可以分成三個步驟：一、把I_2i-1和I_2i比較， $i=1,\cdots,\lfloor\frac{n}{2}\rfloor$ ，共比 $\lfloor \frac{n}{2} \rfloor$ 次。每一次比較中，較大的一個我們稱之為勝者，較小的為敗者。二、把第一步中 $\lfloor \frac{n}{2} \rfloor$ 個勝者以Ford-Johnson法整理好。在第二步後， n個物品之間的關係可以用下圖表示：

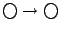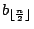此處每一圓圈代表一物品，" $\bigcirc \rightarrow \bigcirc$ "代表左端物品少於右端物品，勝者以 a_i 為名，敗者以 b_i 為名。在 $b_{\lfloor \frac{n}{2}\rfloor }$ 之右有一虛線圓圈，這代表當n為奇數時未參與第一步中比較的I_n（當n為偶數時，此虛圓圈不存在）。第三步要作的事是如何把b_i插到已經整理好的 {a_i} 中。其中 b_i 不需經任何比較即可插到 a_i 之後。FJ 提出的辦法是第三個步驟。

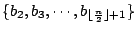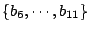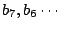三、把 $\{b_2,b_3,\cdots,b_{\lfloor \frac{n}{2}\rfloor +1}\}$ 按照先後次序分為若干組，如{b₂,b₃}是第一組，{b₄,b₅} 是第二組， $\{b_6,\cdots,b_{11}\}$ 是第三組等。然後按照組的次序一組一組的插入a_i中。如何把一組b_i插入{a_i}中呢？仍是一個一個的以中分法合併入{a_i}的次序應為 b₃,b₂,b₅,b₄,b₁₁,b₁₀, b₉,b₈, $b_7,b_6\cdots$ 。何以要規定這樣的次序呢？因為這樣的次序所需比較的數目最少。注意在此次序中，第j組的每一個b_i都只需j+1次比較即可合併 {a_i}。譬如b₃合併入 {b₁,a₁,a₂}，祇需比兩次。在最壞的情形下，b₃小於a₂，則b₂ 要和 {b₁,a₁,a₃}合併，也祇需要比兩次。如果合併的次序是b₂在b₃之前，則b₂合併入{b₁,a₁}固然祇需要比兩次，但b₃和 {b₁,a₁,b₂,a₂}合併就要三次了。讀者可試證FJ所提出的合併次序的確是最好的次序。

令FJ(n)為以FJ法整理n個物品時的保證數，則可算出(參考5)

$\begin{displaymath} FJ(n)=t \lceil\log{\frac{3}{4}t} \rceil-\lfloor \frac{2^{\lf... ... }}{3} \rfloor + \frac{1}{2}\lfloor\frac{1}{2} \log{6t}\rfloor \end{displaymath}$

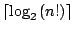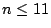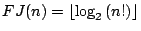比較FJ(n)和S(n)即知對任何一個n，FJ(n)都小於或等於S(n)，同時自1959年FJ提出他們的方法後，也沒有任何一個其它方法在任何一個n上能得到比FJ(n)小的保證數。因此不少人以為FJ法對所有n的而言都是最好的整理法。但是只有在某些n值時，我們可以證明FJ(n)是最小的保證數。證明的方法是利用資訊理論得到任何一個整理n個物品的方法的保證數必不小於 $\lceil \log_2{(n!)}\rceil$ 的結論。在 $n\leq11$ 或n=20,21時， $FJ(n)=\lfloor \log_2{(n!)}\rfloor$ ,因此在這些n值時，FJ法必為最佳法。

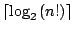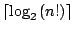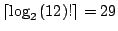在其它的n值時FJ(n)都大於 $\lceil \log_2{(n!)}\rceil$ , 那麼FJ法究竟是否最佳法呢？FJ(n)第一次不等於 $\lceil \log_2{(n!)}\rceil$ 是當n=12時，此時FJ(12)=30, 而 $\lceil \log_2{(12)!} \rceil=29$ 。所以要解答FJ法是否最佳之謎，第一道要攻破的關口就是n=12時。在1965年，Wells（參考8）花了不少的計算機時間，終於算出了整理12個物品最少需要30次，即FJ法在n=12時，仍為最佳法。這一結果大大的增強了認為 FJ 法即最佳法的人的信心，但基本的謎題仍在。

一直到1977年，這個謎題才被解出。Manacher（參考7）證明了在無限多的n值時， FJ(n)都不是最低的保證數。他找到最小的這樣一個n是當n=191時，這時FJ(n)=1192, 而Manacher的方法祇需1191次比較。我們現在來簡略的解釋Manacher的做法。我們知道當n大時

$\begin{displaymath} \log_{2}{(n!)} \cong n\log_{2}{n}-1.443n \end{displaymath}$

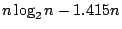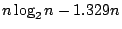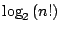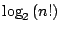而FJ(n)則在 $n\log_2{n}-1.415n$ 和 $n\log_2{n}-1.329n$ 之間循環（參考7）。換句話說，在有些n時，FJ(n) 很接近 $\log_2{(n!)}$ ，因此可能不容易再找到別的一個方法有更小的保證數。但在另一些 n 時，FJ(N) 和 $\log_2{(n!)}$ 相差較大，似乎有改進的餘地。我們把前一類 n 稱為好 n，後一類 n 稱為壞 n。Manacher 的想法是當 n 是壞n時，也許可以找到兩個數n₁和n₂其和為n，而n₁和n₂都是好n。在這情形下，我們可以把整理n個物品的原題分解成兩個子題，其一是整理n₁個物品，其二是整理n₂個物品，最後再把這兩組整理好的物品合併起來。令 M_t (n₁, n₂)為以 t 法併合 n₁ 和 n₂ 個物品時所需的比較則當

M_t(n₁,n₂)<FJ(n)-FJ(n₁)-FJ(n₂)

時，此法即可勝過FJ法。

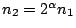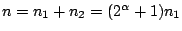這樣的n果然找到了。設n₁為一好n，則 $n_2=2^{\alpha}n_1$ 也是一個好n，但 $n=n_1+n_2=(2^{\alpha}+1)n_1$ 則是一個壞n，這時

$\begin{displaymath} FJ(n)-FJ(n_1)-FJ(n_2) \cong (\alpha+2)n_1-\frac{1}{2}\log_2{n} \end{displaymath}$

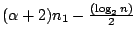問題是有沒有一個方法t在合併n₁和n₂時所需的保證數小於 $(\alpha+2)n_1-\frac{(\log_2{n})}{2}$ ？

在現有的合併法中，最好的一個是筆者和林甡君設計的HL法(參考4)，在合併n₁和n₂等於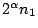 $2^{\alpha}n_1$ 時約需

$\begin{displaymath} HL(n_1,n_2) \cong(\alpha+2)n_1 \end{displaymath}$

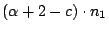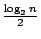次比較。所以HL法還不能達到我們的要求。但是若能略加改進HL法，使得它的保證數變為 $(\alpha+2-c)\cdot n_1$ ，則不管c是多小的一個正數，當n₁夠大時cn₁會比 $\frac{\log_2{n}}{2}$ 大。這是因為

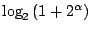$\begin{displaymath} \frac{1}{2}\log_2{n}=\frac{1}{2}\log_2{(n_1+2^{\alpha}n_1)} =\frac{1}{2}\{\log_2{n_1}+\log_2{(1+2^{\alpha})}\} \end{displaymath}$

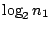其中 $\log_2{(1+2^{\alpha})}$ 是一個常數，而當n₁夠大時， cn₁會比 $\log_2{n_1}$ 大很多。因此改進HL的方法會達到我們的要求。

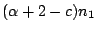在合併兩個集合時，如我們把含較多物的一個集合稱為大集合，含較少物的稱為小集合，則HL法是把小集合中的物品按照已整理好的次序一個接一個的併入大集合中。譬如說我們選了從重到輕的次序，則小集合中最重的一個第一個要合併入大集合中，在此物的合併未完成前，我們不考慮小集合中任何其它的物品。等最重的一物已被合併入大集合中後，則開始第二重物的合併，如此類推。Manacher（參考6）提出的改進法，是把小集合中之物按照次序分為若干組，每組m物。每次合併以組為單位，即一組未合併完成前，不考慮其它組，但同組中的物品可同時進行合併。譬如X和Y兩物同一組，則我們可以第一次比較X(和大集合某物)，第二次比較Y，第三次再比較X等。注意HL法是Manacher法當m=1時的特例。Manacher算出了當m=3或4時，即可顯著改進HL法而達到 $(\alpha+2-c)n_1$ 的保證數。

Manacher法雖然贏了FJ法，但它仍不是最佳法。因此最佳法是什麼成了一個新的謎題。在一些特定的n值上改善Manacher法並不難，但是如何能有一通盤性的改善，則尚待研究。其中的一條路是徹底瞭解合併n物和m物時，特別是當m很小時，最小的保證數是什麼？令f_m(k)為一滿足下列條件的n值：合併f_m(k)和m的保證數為k，但合併f_m(k)+1和m的保證數為k+1；換句話說f_m(k)是最大的一個n值還可以在k次比較內保證和m合併完成。如果對每一個k，我們都解出了f_m(k)則對每一個n合併n與m的保證數也必可算出。我們所以要定義f_m(k)，是因為我們的結果以f_m(k)這個函數來表示比較簡單。現在所知的f_m(k)非常有限，約有以下數類：

1.f₁(k)=2^k-1

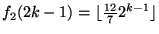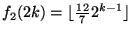2. $f_2(2k-1)=\lfloor\frac{12}{7}2^{k-1}\rfloor$ ， $f_2(2k) = \lfloor \frac{12}{7} 2^{k-1} \rfloor$ （參考2,3）

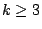3.當 $k \geq 3$ 時，

$\begin{eqnarray*} f_3(3k) &=& \lfloor\frac{43}{7}2^{k-2} \rfloor -2 \; , \\ f_... ...\; , \\ f_3(3k+2) &=& \lfloor\frac{12\cdot 2^k-6}{7} \rfloor -1 \end{eqnarray*}$

這個結果是筆者獲得的，證明約需二、三十頁，m=4 的情形其繁複可能要十倍於此。

筆者以一個未解的疑破案當作本文結尾。令 M(n,m) 代表合併 n 與 m 所需最小的保證數，且 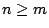$n \geq m$ ，試證：

$\begin{displaymath} M(n,m+1)\geq M(n,m) +1 \geq M(n+1,m) \end{displaymath}$

筆者提供臺幣四仟元給第一個解出此題者。

: (1)Ford, L. R., Jr. and Johnson, S. B., 〈A tournament problem〉, Amer. Math. Monthly 66(1959),387-389.
: (2)Graham, R. L., 〈On sorting by comparison〉, Proc. 2nd Atlas Conf., 1971.
: (3)Hwang, F. Nd Lin, S., 〈Optimal merging of two elements with n elements〉, Acta Informatica, 1(1971), 145-158
: (4)Hwang,F. and Lin, S., 〈A simple algorithm for merging two disjoint linearly-ordered sets〉, SIAM J. Comput. 1(1972),31-39.
: (5)Kunth, D., 《The Art of Computer programming》, Vol. III, Addison-Wesley, 1973, 181-209.
: (6)Manacher, G., 〈Nontrivial improvements to the Hwang-Lin merging algorithm〉, to appear in J. ACM.
: (7)Manacher, G., 〈The Ford-Johnson algorithm is not optimal〉, to appear in J. ACM.
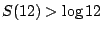: (8)Wells, M., 〈Note on the fact that $S(12)>\log{12}$ !〉, proc. IFIP 65 Congress, vol. 2, 1965, 497-498.
: (9)Steinhaus, H., 《Mathematical Snapshots》, Oxford Univ. Press, 1950, 38-39.

對外搜尋關鍵字：
．整理
．合併
．Steinhaus
．資訊理論
．Euler


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：朱安強

最後修改日期：4/26/2002