機率一講

．原載於數學傳播第二卷第三期
．作者當時任教於台大數學系

‧註釋

機率一講

楊維哲

機率論的一個發源地是記述統計學；明瞭記述統計學的概念，對於機率論的學習，大有助益！

$\S$ 1. 假設我擔任一班數學課；共有50位學生，現在考慮某次月考的成績；我們用 x_n 代表第 n 號學生的成績。所以就有一堆數據：x₁, x₂, x₃,…,x_N，（此地 N=50）。我們用 X 來代表這個統計數據。所以，事實上 X 是映射： $1 \rightarrow x_1$ ， $2 \rightarrow x_2$ ，… …；不是集合 {x₁,x₂,…,x_N}； ──例如，這集合的元素個數可以小於 N，而且，若是看成集合，則

「1 號得 70 分，2 號得 81 分」

與

「2 號得 70 分，1 號得 81 分」

並無區別；但是，就學生的立場，這當然有區別，對於老師，區別就不大！倒是有幾個人 81 分，幾個人 70 分，還有點區別！

還有，要記住的一點是：X 的定義域，此地是 1 到 50 之自然數，這不太重要。

$\S$ 2. 記述統計學的最初的問題，可以很具體地這樣子來說明。如果校長問我：「他們這次月考考得怎麼樣？」，我該怎麼報告？

對於學生的家長，我要答以他子女的成績就好了；對於校長，一個個學生的成績他卻不會耐煩聽；他要知道最重要卻也最起碼的兩件事：甲、大體如何？乙、是否參差不大？（也許該考慮「能力分班」？……）。

校長不一定滿意於一個籠統的，（定性的）說法，如「大體很好，參差不大」，他要一個更精確的，（定量的）說法；於是，我要給他兩個數字：甲、代表值 ¹ 。乙、參差度 ² 。

$\S$ 3. 我先強調兩點：

: 一、通常人只想到甲，那太粗魯了！顯然乙也很重要。
: 二、統計數據本身才是完整的資料；（古典的）記述統計就是需要 X 這麼完整的資料，而（近代的）統計並不肯花精力得到它。（通常是做不到，太貴了。）無論如何，從 X 變成兩個數值，顯然是資訊 (information) 的大大濃縮（或損失）。對於某些事或某些人（如校長），這剩下的資訊就很夠用了。對某些事，這卻不夠。

$\S$ 4. 如何取代表值 α，及參差度 β？

通常採用

$\begin{eqnarray*} \alpha &=& \mbox{{\fontfamily{cwM2}\fontseries{m}\selectfont \... ...1pt{\fontfamily{cwM4}\fontseries{m}\selectfont \char 207}}(S.D.) \end{eqnarray*}$

的制度，於是，對於校長的報告，就是「本班本次月考成績為 $A.M.(X)\pm S.D.(X)$ 」。

$\begin{eqnarray*} A.M.(X)&\equiv&\sum_1^N\frac{x_i}{N}\\ S.D.(X)&\equiv&\sqrt{N^{-1}\sum[x_i-A.M.(X)]^2}\\ &=&\sqrt{{\mbox{Var}}X} \end{eqnarray*}$

$\begin{eqnarray*} \mbox{{\fontfamily{cwM1}\fontseries{m}\selectfont \char 106}\h... ...us0.1pt{\fontfamily{cwM1}\fontseries{m}\selectfont \char 106} }) \end{eqnarray*}$

我必須再強調這一點：採用這種「 $A.M.\pm S.D.$ 」制，是最常見的，（甚或是最方便的）制度。但是它一點兒也不是唯一的制度。事實上這情形有一點兒像橋牌的叫牌制度：你可以隨便發明一套，只要說清楚你的制度。

$\S$ 5. 在計算和式中，我們當然可以聰明一點，不必 x₁ + x₂ + x₃ + $\cdots\cdots$ （慢慢加），而可以採用（Lebesgue 式的想法！）

$\begin{displaymath} \sum x_i\equiv\sum_x x\cdot (\mbox{{\fontfamily{cwM2}\fontse... ...us0.1pt{\fontfamily{cwM1}\fontseries{m}\selectfont \char 98}}) \end{displaymath}$

括弧中的叫做了 X=x 之頻率 (frequency)。它的意義很明白，遠比它的表達式子容易！事實上我們計算 $N^{-1}\sum$ 的機會更多，因此，把頻率用總頻率 N 去除，叫做相對頻率 (relative frequency)，記做 f，則得

$\begin{displaymath} A.M.(X)\equiv\sum_x x\cdot f(x) \end{displaymath}$

請注意：若 φ 是個 $\mathbf{R} \longrightarrow \mathbf{R}$ 之函數，用 $\varphi(X)$ 代表統計數據

$\begin{displaymath} (\varphi(x_1), \varphi(x_2), \varphi(x_3), \cdots, \varphi(x_N)) \end{displaymath}$

則 ³

$\begin{displaymath} A.M(\varphi(X))=\sum_x\varphi(x)\cdot f(x) \end{displaymath}$

$\S$ 6. 我們馬上可以導出一個重要的定理，這定理的內涵太容易了，雖然其表達式反倒較煩。所以我們就用「我們班」的例子來說明：

考試成績，當然在 0 與 100 之間： $0\leq x_i\leq100$ ；（此地上限 100 不重要）。今設平均為 23 分，則全班 50 人中，分數超過 46 分的，一定不到一半（25 人），全班分數超過 69 分的，一定不到 16.66… 人〔故意這麼寫，人數不能有小數！〕，分數超過 92 分的，不到 12.5人……。

這就是著名的（而且也幾乎無聊的，trivial）Markov 不等式。

定理：若一切 $x_i \geq 0$ ，[單書作 X $\geq$ 0]， $\mu = A.M.(X)$ ，k>1，則

$\begin{displaymath}f\{X>k\mu\}<k^{-1} \; ,\end{displaymath}$

當然也有

$\begin{displaymath}f\{X\geq k\mu\}\leq k^{-1}\end{displaymath}$

我想證明就可以省了；由「我們班」的例子就很明白了！

倒是必須註解一下：

1 定理中，k>1 可以改為 k>0，因為 $1\geq k>0$ 時，這不等式就「無聊地成立！」(trivially true)

2 若不是利用相對頻率 f 之概念，則定理的數學表達式就麻煩了，要寫成

$\begin{displaymath} \frac{\{i:x_i>k\mu\}\mbox{ {\fontfamily{cwM1}\fontseries{m}\... ...ily{cwM1}\fontseries{m}\selectfont \char 98} }}{N}<k^{-1} \; , \end{displaymath}$

這不但煩（繁），而且意思反倒不清楚！

$\S$ 7. 在上一定理中當然我們必須假定 $X\geq0$ ，（即 $x_i \geq 0$ ，一切 i）。你該造個例子說明「在 X<0 時，敘述（可以）為誤」，不過，不論 X 為何，令

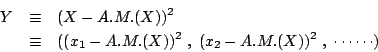
$\begin{eqnarray*} Y & \equiv & (X-A.M.(X))^2 \\ & \equiv & ((x_1-A.M.(X))^2 \; , \; (x_2-A.M.(X))^2 \; , \; \cdots\cdots) \end{eqnarray*}$

則 Y 就是個統計數據，恆非負，因此 Markov 不等式對 Y 適用！也就是說：對 k>0，（其實 k>1 才有聊！）

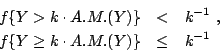
$\begin{eqnarray*} f\{Y>k\cdot A.M.(Y)\} &<& k^{-1} , \\ f\{Y\geq k\cdot A.M.(Y)\} &\leq& k^{-1} \end{eqnarray*}$

但是，照定義，

$\begin{displaymath}A.M.(Y)={\mbox{Var}}X=(S.D.(X))^2\end{displaymath}$

而且記 $k\equiv l^2$ , l>0，則得

$\begin{displaymath}f\{(X-A.M.(X))^2>l^2\cdot(S.D.(X)^2)\}<l^{-2}\end{displaymath}$

但是

$\begin{displaymath}(X-A.M.(X)^2>l^2\cdot(S.D.(X))^2)\end{displaymath}$

就等於

$\begin{displaymath}\vert x-A.M.(X)\vert>l \cdot S.D.(X).\end{displaymath}$

因此有(Chebyshev 不等式)：

$\begin{displaymath}f\{\vert X-A.M.(X)\vert>l\cdot S.D.(X)\}<l^{-2} \; ,\end{displaymath}$

或

$\begin{displaymath}f\{\vert X-A.M.(X)\vert\geq l\cdot S.D.(X)\}\leq l^{-2}\end{displaymath}$

我們在這裏打住，不再講記述統計了，就轉到機率論來！

$\S$ 8. 我想先把主題點出來：機率論和記述統計，幾乎完全一樣！只是一虛一實而已。

為了說明這一點，我們想像這種情形。去年我做了完整的紀錄弄成一張張卡片，到了這一年度，我決心做個不負責的老師：若你是個學生，我請你抽一張卡片，就當做你的分數。

這麼一來記述統計就成了機率論了！如果，去年有 4 個人分數不到五十分，那麼，

$\begin{displaymath}f\{X<50\}=\frac{4}{50}=0.08\end{displaymath}$

現在，你的分數不到五十分的機率就是 0.08，換句話說，「相對頻率」改成「機率」，用符號 P 表示：

P{X<50}=0.08

如果去年有 6 個人不及格，即 f{X<60}=0.12，則現在你不及格的機率是 0.12，即

f{X<60}=0.12

當然，現在的 X 從「統計數據」改成了「隨機變數」，隨著機會（你的運氣）而變的數；另外，「算術平均」A.M.，也改成（數學）期望值 E；如果去年全班平均為 A.M.(X)=74 分，則你（現在）的期望值就是

E(X)=74 .

換句話說，我們有個簡單的小字典來對照這兩種語言：

記敘統計學	機率論
相對頻率 f	機率 P
統計數據	隨機變數
算術平均 A.M.	期望值 E.
方差 ${\mbox{Var}}.$	方差 ${\mbox{Var}}.$
標準差 S.D.	標準差 S.D.
以下兩國語言大致相同

$\S$ 9. 為什麼說記述統計與機率是一實一虛呢？我造了 50 張卡片，當這是記述時，這是很真實的東西（這是我教學的成果），X 代表這 50 張，張張皆實。反過來，你要抽一張，我讓你先看過一遍，有兩張 98、一張 92，……，但，只有你抽到的那張才是真實的，所以，X 只代表那一張。在記述統計，如果 A.M.(X)=84，或者 f{X<60}=0.02（只有一人不及格），顯然我這老師教得不錯；若改成機率，則 E(X)=84，或 P{X<60}=0.02，只是你的機會不錯，期望值很高，或者，不及格的機會只有50分之一。

可是，我們已經強調過了，這機率是虛的。萬一（其實不是「萬一」，而是「五十一」），你抽到那張不及格的卡片，那麼 X<60。（例如 X=50 吧），妳的運氣不好，那麼這些期望值，或機率，都幫不了你的忙！說「我及格的機率高達 98 $\%$ 」，或者我分數之期望值為 84 都喪失意義了。在你抽卡之前有意義，但抽了卡片，X 是多少，就多少，如果 X=50，那麼 P{X<60}=0.02 及 E(X)=84 都是自欺欺人的安慰。

$\S$ 10. 那麼機率的意義是什麼？當然機率很大（接近 1）很小（接近 0）有它的意義，我們也承認這可以有不同的見解。不過我認為這和「近似值」的情形一樣，對於每一個具體的情形，自然有它具體的意義。所以，我們不打算花精神來解釋「很可能」跟「很不可能」，把它們當做是不須要解釋的，就跟「近似」之不要解釋一樣。

那麼我們怎麼解釋「一事件之機率為 p」呢？我贊成 Bridgeman 的運作觀 (operationalism)，所以我找採大數法則來解釋。

（弱）大數法則：假設一事件 A 發生之機率為 p，假設我們能夠一再地重覆我們的實驗，觀察同樣的現象，每次的佈置都相同（機會相同），而且一次次之間互相沒有關聯，作了 n 次，其中有 k 次發生了這件事件；我們計算發生的相對頻率 $\frac{k}{n}$ ，那麼，在 n 趨近無限大時，這相對頻率 $\frac{k}{n}$ 就趨近於 p，（說得客氣一點）「 $\vert(\frac{k}{n}-p)\vert$ 不很小」的機會很小！

我們先強調一下：不能重複（獨立）地作實驗的事情，講機率不太有意義！

我再把上述的大數法則推廣一下：

定理：假設 X₁, X₂,…,X_n 是隨機變數，互相獨立，而且機率分佈相同，那麼，

$\begin{displaymath} \lim_{n\rightarrow\infty}\frac{X_1+X_2+\cdot+X_n}{n}=E(X_i) \end{displaymath}$

$\S$ 11. 我該說明前一敘述只是後一敘述的特殊情形！──規定 A 發生時，X=1，A 不發生時 X=0，那麼 X 是隨機變數，我們可以作出獨立，而且機會的狀態全同的 X₁,X₂, $\cdots\cdots$ ,一樣，P(A)=p 就是 E(X_i)=p，故前一敘述是後一敘述之特例。

應用：如果你知道 E(X)=84，較安全的辦法是請老師（我）同意：抽很多次，（雖則我規定抽出來要放回去重新抽）。用它們的平均 $\frac{(X_1+X_2+\cdots+X_s)}{s} = Y_s$ 做為你的成績。如此可以保證這個平均會很接近 84。──不接近 84 的機會很少。

對外搜尋關鍵字：
．Lebesgue
．Chebyshev不等式
．機率論
．隨機變數
．期望值
．大數法則
．算術平均
．標準差
．方差

後註

通常的大數法則，都再加上些不必要的條件，這些條件雖然不必要，但在初學時，是很有利的〔假設 ${\mbox{Var}}X_i=\sigma^2<\infty$ 〕。這證明可在拙著《普通數學》中找到，大意如下：

由於諸 X_i 互相獨立，

$\begin{displaymath} {\mbox{Var}}(\Sigma_1^s X_i)=\Sigma_1^s {\mbox{Var}}X_i=s\sigma^2, \end{displaymath}$

故

$\begin{displaymath} {\mbox{Var}}Y_s = s^{-2} \cdot s\sigma^2 = s^{-1} \sigma^2 ... ...ntseries{m}\selectfont \char 231}} s \longrightarrow \infty) ; \end{displaymath}$

由 Chebyshev 不等式

$\begin{displaymath} P\{\vert Y_s-\mu\vert\geq\varepsilon\}=P\{\vert Y_s-\mu\vert\geq k\cdot\sqrt{s^{-1}\sigma^2}\}\leq k^{-2} \end{displaymath}$

$\begin{displaymath} k=\frac{\varepsilon\sqrt{s}}{\sigma} \rightarrow \infty \qua... ...1}\fontseries{m}\selectfont \char 231}} s \rightarrow \infty), \end{displaymath}$

故 $P\{\vert Y_s-\mu\vert\geq\varepsilon\} \rightarrow 0$


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：黃信元

最後修改日期：4/26/2002