泰利斯 (Thales)
──天文學家、數學家;公元前 624?∼546?
泰利斯生於希臘麥爾塔斯,青少年時代他過的是商人的生活。曾經南渡埃及做生意,在留居埃及期間,由埃及神宮處獲得多數學天文的知識。不久,其知識就遠超過神官了。泰利斯以此知識用來測量金字塔的影長,得出金字塔的高度,在當時曾驚動國王阿馬西斯 (Amasis) 而著名,他在埃及的時候,對於數學、天文學均極感興趣,回到希臘後仍繼續此研究,隨著成為世界上最早的大數學家,據傳而他曾預言公元前585年5月28日有日蝕,他說:「5月28日雖在晝間,陽光卻會消失,而突然變成黑夜,且天空將有星星閃爍。」當時沒人相信他的話,等到5月28日,事實證明了他預言的正確;當日太陽懸空,由逐漸起缺口,而到其光全失,人們才發現泰利斯是對天文學知識最豐富的一個人。
還有一故事說,當時正有兩國在交戰,戰爭正進行得如火如荼的時候,依泰利斯的預言,太陽的光輝,在白晝間突然消失,隨著有人說:「我們因戰爭在持續,大概引起神發怒了,宜及早停戰向神陪罪才行」,因而鳴金收兵言和,訂定和平條約。
有一次的晚上,泰利斯在天晴月當空之際,遙望天際閃爍的星星,渾然不知自己,而掉進水溝裏去。此時有位老婦人說:「泰利斯先生自己都不知算其腳步,為什麼會知道那麼遙遠的星球呢?」
泰利斯在年輕行商的時候,最著名的一則小故事是這樣的:有人訂購食鹽,泰利斯每次都將食鹽裝載在一隻驢背上送去,途中需經過一條小河,有一天當他們行將渡小河之際,不意此驢腳被石頭絆了腳,而跌入水中,食鹽也因而有一大半流失,泰利斯雖受損失,但驢子卻覺得比絆倒前之行李輕得多而暗自高興,這隻驢子體會到此法還管用,乃每次一到此小河,就重施故技,以期減輕它的負荷。因此泰利斯乃心生一計,以海棉置於驢背上,等驢子故意摔跤時,因海棉吸水,負荷就比原來帶的食鹽更重了,此後驢子就不敢貿然地再故技重施了。
泰利斯發見不少幾何的定理。如下列
- (1)對頂角相等。
- (2)等腰三角形的兩底角相等。
- (3)兩三角形若有一內角及夾此角之兩邊分別對應相等,則兩三角形全等。
- (4)兩三角形若有二內角及此兩角所夾之一邊分別對應相等時,則兩三角形全等。
- (5)在圓上一點,連直徑之兩端所成之二弦互相垂直。
泰利斯利用定理(3),測量兩點間,隔有山或池塘而無法直接量的距離。(如圖十一)他的方法是由 A,B 望一可通的一點 O,連 AO 並延長至 C 使 AO=OC,
其次連 BO 並延長至 D 使 BO=OD。此時兩三角形 AOB 與 COD 中
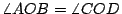 (對頂角,定理(1)),且作圖 AO=OC,BO=OD,故 (對頂角,定理(1)),且作圖 AO=OC,BO=OD,故 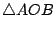 與 與 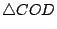 全等,而得實測 CD 便知 AB 之長了。 全等,而得實測 CD 便知 AB 之長了。
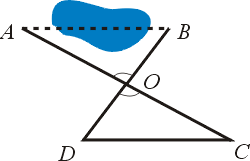
圖十一
|
圖十二
|
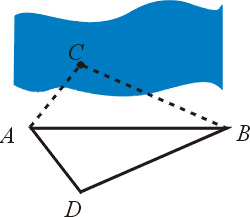
泰利斯用定理(4),從岸上一點 A 欲測河中一船 C 的位置時,他就先取岸上另一點 B,並由 A,B 觀測船 C 所得的角 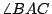 與 與 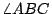 再於岸上作 再於岸上作
來決定點 D。(如圖十二)此時 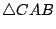 與 與  有兩內角及其夾邊對應相等,故兩三角形全等,於是得 AC=AD。但 AD 在岸上可實測,故由點 A 望船 C 位置的距離也就可得了。 有兩內角及其夾邊對應相等,故兩三角形全等,於是得 AC=AD。但 AD 在岸上可實測,故由點 A 望船 C 位置的距離也就可得了。
又利用定理(5)可由直線 l 上一點 A 引一直線與 l 垂直,事實上過點 A,B 可任作一圓,連直徑 BC 之另一端 C 與點 A 所得之直線就是與 l 垂直之線。(如圖十三)
定理(5)雖說是泰利斯發明,但也有人認為是畢達哥拉斯所發現。
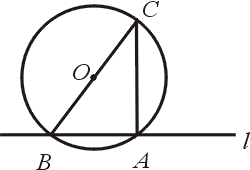
圖十三
|
|