黃光明

我們先舉一個典例的組合學問題來瞭解組合學探討的到底是什麼：「拿一張白紙；任意把它劃分成 n 個區域，而且兩個鄰近的區域必須共邊而不僅共點。 每一個區域著上一種顏色，條件是相鄰的兩區域不能同色，問如果給你四種顏色的話是否一定夠？」組合學的問題常常是如此。 先規定了一件要做的事，像以四種顏色給區域著色，這件事多半都是很容易做的而且有各種各樣的做法，但我們同時加上了一些條件，像鄰近的區域不得同色。 現在有些做法合於條件有些不合條件，我們問合於條件的做法有多少種，或者問有沒有合於條件的做法（如所舉例題），或者要找出一種好的做法。

上面所舉的例題雖屬典型卻並不平凡，它是有名的「四色」問題，相傳是數學當今三大難題之一（另外兩個是「Riemann假設」和「Fermat最後猜測 ^註1 」）。 一百多年來，不知多少數學家為之絞盡心血，一直到今年七月間才得到了肯定的解答，相信大家都已在報章上讀到有關的報導，這裏不再重複。 但我們還要借四色問題來介紹一個有用的觀念-「圖形」。圖形學是組合學裏非常重要的一支。

一個圖形是一個點的集合和一個定義在兩點上的線的集合，（因此任何兩元性的關係都可以用圖形來表示，這就是為什麼圖形學之應用如此廣泛。） 譬如在四色問題裏，把每一個區域當成一點，如果兩個區域相鄰則對應的兩點間連一條線（如不相鄰，則無線），則 n 個區域即可以一圖形表示，而且因為在四色的問題裏，區域的大小，形狀，相隔的遠近等等都和問題沒有關係， 唯一有關係的是兩區域是否相鄰，而這一個關係表現在我們的圖形裏。因此以圖形代表原圖，並沒有失去任何價值。 原來的問題也可改在圖形上問：如給每一點著色，有線相連的兩點不得同色，四種顏色夠不夠？

因為在原題中，紙上的兩個區域不會互交；因此化為圖形後，也一定可以使線和線間互不相交，這樣的圖形叫做平面圖。 有的圖形雖然有兩線相交（圖一），但若換一種畫法（圖二）就可不相交，而線的集合不變，則也算是平面圖。

圖一

圖二

但如圖三和圖四的圖形無論怎麼畫，都一定有線相交，故不是平面圖。

圖三

圖四

我們怎樣分辨那些是平面圖，那些不是呢？Koratowski 證明了，如果一個圖形裏不含圖三或圖四則為平面圖，反之則不是平面圖。看！這是一個多漂亮的定理，數學的美就在這些「巧」和「妙」上。

一個圖形如果是平面圖，則四種顏色一定夠著色；如果不是平面圖則一定不夠。近二十年來組合學上另有三大疑案被破獲。 第一是流傳了近二百年的 Euler 在拉丁方陣上的猜測被證為非。第二是也有一百多年歷史的「Kirkman 女學生問題」被證有解，先說前者。

一個序 (order) 為 n 的拉丁方陣是一個 n x n 的方陣，每一行每一列所含的元素都構成 這個集合。 如圖五和圖六是兩個序為三的拉丁方陣：

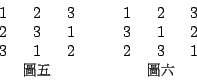
當 n 大於一時 Euler 發現，除了 n 是 4k+2，k=0,1,2,… 這一型數字外，正交的拉丁方陣都存在。 於是他猜測當 n=4k+2，k=0,1,2,… 時沒有正交的拉丁方陣存在。在二十世紀初葉，有一個人把所有序為六的拉丁方陣都列出試著搭配，果然找不到互相正交的兩個，更增加了 Euler 猜測的可靠性。

約二十年前，兩個印度人 Bose 和 Shrikhande 和一個美國佬 Parkor 分別找到了序為十的正交拉丁方陣。 不久後他們又攜手合作找到了一個方法可以造所有 n=4k+2 的正交方陣，只要 n 大於 6，徹底地摧毀了 Euler 的猜測。他們的發現據說是紐約時報第一次在頭版上刊發有關數學的報導。

Kirkman 女學生問題是這樣的：有 6k+3 個女學生，每天三個一排地出去散步。所以每天每個人有二個同排的伴侶。 如果我們希望每兩個女學生都同排一次，則最少需要 3k+1 天。 問題是否一定有一個排法在 3k+1 天內任何兩個女學生都同排一次，圖七是一個 k=1 時的排法：

有不少人為不同的 k 值做出了排法，但俄亥俄州立大學的博士班學生 Wilson 和他的導師 Chauduri（印度人）在1971年串上了最後的一鏈而證明了 Kirkman 女學生問題對所有的 k 都有解。 一百多年來的猜疑至此塵埃落定。

拉丁方陣問題和 Kirkman 女學生問題在組合學上都屬於叫做「數學設計」的一門學問。數學設計中最基本而廣泛應用的一種叫做「區間設計」。 假設我們有一個含 v 元素的集合 S。 另外有一個含 b 區間的族 F，F 族裏每一區間都是 S 的一個 k 元素的子集合。且 S 中任二元素 都在 F 中出現於 r 個區間裏，S 中任二元素都同時出現於 F 中 λ 個區間裏，滿足這樣條件的 F 稱為一個 區間設計。

圖八是一個 (9,12,4,3,1) 的區間設計：

S 裏的元素在 F 裏一共出現多少次？有兩個答案：S 共有 v 元素，每一個元素出現 r 次，故共出現 vr 次；但同時 F 有 b 區間，每一區間含 k 元素，故共出現 bk 次，所以 vr=bk。

再問 S 裏的一對元素同時出現在 F 裏的一個區間共有多少次呢？也有兩個答案：S 共有 對元素，每一對出現 λ 次，故其出現 次；但同時 F 有 b 區間，每一區間含 對元素（k 中任取二），故其出現 次，故得

以上兩個方程式是一個區間設計必需滿足的條件，但是不是充分條件呢？Hanani（以色列人）證明了當 k=3 或 4 時，它們是充分條件，而當 時則否。 當 時，什麼是區間設計的充分必要條件還是一個謎。通常用來構造區間設計的方法是「有限幾何」，「差數集合」，「Galois 域理論」等。

下面我們介紹組合學上兩個有趣且有用的定理。

世界上任意選六個人，以六點代表之，然後問每兩個人彼此是否認識，如果認識則讓兩點間達一線，如不認識則無線。 則下列兩者必有一為真：

(1)某三點間彼此有線， (2)某三點間彼此無線。

如果選比六個人多時，也必定會有以上結果（因為只要看其中任六點間的圖形就夠了），但選比六點少時，則沒有這種結果。譬如圖九中的五點既無三點彼此間有線也沒有三點彼此間無線：

圖九

我們也可以利用以上的結果做一個兩人的遊戲。先在紙上畫下六角形的六頂點，然後兩人輪流在頂點間連線，連線時可以任意用一支紅筆或一支藍筆，誰在連線後造成了一個三邊同色的三角形者為輸家。 根據以上結果，在所有的線都被連完後必定有一個同色三角形出現（可以把紅色三角形當成三點間彼此有線，藍色三角形當成三點間彼此無線），故必定有一輸家。

廣義的Ramsey定理說： 現有一個 N 點的集合 S、把 S 中所含 r 點的子集合分成互不相 交的 k 組 S₁,…,S_k。設 l₁,l₂,…,l_k 為 k 個不小於 r 的數，則當N不小於 n_r (l₁,l₂,…,l_k)（後者稱為一個 Ramsey 數）時，下列的陳述對於某一個 i 而言，i=1,…,k, 必為真：

「S 中有某 l_i 個元素的集合 ，其任意 r 點的子集合都在 S_i 這一組內。」

這個定理有點不容易瞭解，回到原例題，S 是一個 N 點的集合，所有二點的子集合可分成有線和無線的兩組 (r=2,k=2)。 l₁=l₂=3，n₂(3,3)=6，當 時（例題中 n=6），必有三點其中任兩點間都有線或必有三點其間任兩點間都無線。

Ramsey 定理祇說 Ramsey 數一定存在，卻不告訴 Ramsey 數是多少。譬如我們知道 n₂(3,4)=9, n₂(4,4)=18, n₂(4,5) 以上即不知道了。

著名的數論家和組合學家 Erdös 和 Turan（皆匈牙利人）在四十年前研究一個形式上很不一樣但實質上和 Ramsey 定理頗有關的數論問題：設R為任意一個正整數所成的無限集合且 R 的密度大於零，即對任意 n，

其次我們介紹 Hall 定理。我們要把 n 個女孩和 n 個男孩配成舞伴，我們問每一個女孩那幾個男孩她願意接受為舞伴。設 S 為男孩的集合，則每一個女孩的回答是一個 S 的子集合。現在我們要在每一個子集合裏挑出一個元素（即選出一男孩作該女孩的伴），但是 n 個子集合所挑出的元素必需不重覆（一個男孩不能作兩個女孩的舞伴）。問在什麼情形下挑選可以成功。首先我們看看成功的必要條件。如果有某 k 個子集合的聯集其所包含的元素少於 k 則顯然挑選不能成功，因為找不到 k 個男孩分配給這 k 個女孩。Hall 證明了這個必要條件也是充分條件。Hall 定理有各種態式的表現方式和條件略異的變形，它被應用在作業研究的分派問題上，電話交換網路的操作上及很多其他地方。

下面我們介紹兩個圖形學上的未解題，這兩個問題和四色問題曾被圖形學大師 Hardy 合稱為圖形學上當今三大難題。

第一個問題是問一個圖形是否含有一個 Hamiliton 圈，這個圈的定義我們等一下再給。先談一個有關的，但已在二百年前被解決的問題。就是一個圖形是否有一個 Euler 圈，這也是歷史上第一個圖形的問題。

圖十

Königsberg 這個區域被河流劃分為 A,B,C,D 四區（見圖十），有七座橋溝通區際的交通。問能否從某一區出發，每一座橋經過一次且僅一次而回到原區。

把每一個區以一點表示，每一座橋以一條線表示，則得圖十一。如果從任一點出發，每條線經過一次且僅一次回到原點，稱為一個 Euler 圈。

圖十一

與一個點相接的線的數目稱為該點的度數，很顯明的，如果有任一點它的度數是奇數，則 Euler 圈不可能存在。Euler 證明了這一個必要條件也是充分條件。

如果從一點出發，每一點經過一次且僅一次而回到原點稱為一個 Hamilton 圈。 一個圖形含有Hamilton圈的充分必要條件還是未知。原則上線越多，Hamilton圈存在的機會越大。 到現在為止最好的充分條件是：

1.圖形必須為一連接圖形，即沒有孤立部分。

2.如果每個點的度數照大小次序排列為

則 d₁ 需不小於 2，且對所有不大於 n/2 的 i，不是 ，就得 。

第二個問題叫做「Ulam 猜測」。一個圖形裏度數為 1 的點叫做終點。設圖形 G 中有 k 個終點，令 G_i 為從 G 中拿走第 i 個終點及接它的線所得之圖，從 G 當然很容易得到 (G₁, G₂,…,G_k)。 Ulam 猜測說從 (G₁,G₂,…,G_k)，G 可以被唯一決定。當圖形 G 是一棵「樹」時，即 G 中任意兩點只有一條路線連接（這路線可以經過別的點），Ulam 猜測已被證為真，但對一般的圖形還是一個未解題。