.原載於數學傳播第一卷第三期
.作者當時任教於台大數學系
姚景星;劉睦雄
|
.原載於數學傳播第一卷第三期 .作者當時任教於台大數學系 | |||
|
賽局淺說
姚景星;劉睦雄 |
|
在現今激烈競爭的社會中,賽局理論 (Game Theory) 因應而生。其理論為 Von Neumann 於1928年所奠基。 當時,他的研究並不受到重視,直到1944年《Theory of games and economic behavior》一書問世才受到廣泛注目。 那麼,賽局到底是什麼?首先,我們來看如下二人「零和賽局」的例子,這可以說是孩提時代的遊戲。
例 1:設二人猜拳,各按己意同時出剪刀、石頭、布之一種,來作打賭。(當然猜拳以前彼此不知對方出什麼),則第一人可採用之策略的集合為
我們以
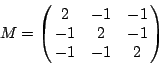
表示償付矩陣。而以 (X,Y,M) 表示此二人零和賽局。我們要研究的問題是「以何種方式打賭時,對這兩人均合算」的問題。
賽局為多數(上例為二人)之競爭者間之競爭 (play) 以形式的構造表示之一組規則,一般需要滿足如下三條件:
競爭者之策略 (strategy) 為於賽局中競爭者可使用之手段(如例 1 之石頭,布、剪刀),且
譬如例 1 競爭者有 2 人,第一人贏 2 元時第二人輸 2 元,第一人輸 1 元時第二人贏 1 元,故二人之償付和均為 0,即上例1為二人零和賽局。
限於篇幅,本文只研討二人零和賽局。如上例 1 二人零和賽局須要知道二人之各策略之集合 X,Y 及二人之償付矩陣,即要知道定義於 X x Y 上之實數函數 M(x,y),
例 2:設二人作下列之打賭,第一人可採用之策略之集合為 X={x1,x2,x3,x4},第二人可採用之策略之集合為 Y={y1,y2,y3},償付辦法約定如下(表 2),
得二人零和賽局 G=(X,Y,M),X,Y 中之策略通常稱為單純策略。償付矩陣中之數目表示第一人之所得,正數表示第一人由第二人可得之金額,負數表示第一人輸之金額,例如 M(x1,y1)=-70 表示第一人採用策略 x1,第二人採用策略 y1 時,第一人輸給第二人 70 元,亦即第一人所得 -70 元,又 M(x3,y1)=3 表示第一人採用策略 x3,第二人採用策略 y1 時,第一人可由第二人得 3 元。二人各按己意同時提出策略(當然二人現出前均不知道對方採用什麼策略),其結果按償付辦法付款。由表 2 之償付矩陣好像此打賭對第一人不利,你希望當第二人嗎?
我們現在考慮此二人零和賽局之解,用償付矩陣中之數目表示第一人之所得,故第一人希望數目越大者越好,反之,第二人希望數目越小越好。因賽局 G=(X,Y,M) 中之 X,Y,M 是公開給競爭者,所以賽前可利用此情報研討採用如何策略較佳的問題。第一人採用 x1 時其最差之所得為
![\begin{eqnarray*}
\max_x\min_yM(x,y) &=& \max[M(x_1,y_1),M(x_2,y_3),M(x_3,y_2),M(x_4,y_2)] \\
&=& M(x_3,y_2)=2
\end{eqnarray*}](img17.gif)
第二人希望採用他的最大損失(最保守之損失)中為最小之策略即 ![\begin{eqnarray*}
\min_y\max_xM(x,y) &=& \min[M(x_2,y_1),M(x_3,y_2),M(x_4,y_3)] \\
&=& M(x_3,y_2) = 2
\end{eqnarray*}](img18.gif)
因此, 此賽局有解,即第一人之最佳策略為 x3,第二人之最佳策略為 y2,此賽局之值 VG=2,即第一人贏定 2 元,誰不照此最佳策略誰就不利。例如第一人懂得這原理,第二人不明瞭時第一人一定採用最佳策略 x3,第二人不知道第一人會採用那一個策略,若第二人採用 y1 或 y3 時損失 M(x3,y1)=3、M(x3,y3)=4 均比採用最佳策略 y2 之損失 M(x3,y2)=2 為大,反之若第一人不明白此原理,第二人知道時,第二人一定採用最佳策略 y2,第一人因不知第二人會採用那一個策略,若第一人不採用最佳策略 x3 時其所得各為 M(x1,y2)=-6, M(x2,y2) = -5、 M(x4,y2)=-80 均比採用最佳策略和之所得 M(x3,y2)=2 為小。亦即誰不採用最佳策略誰就不利,此賽局第一人贏定 2 元,所以第二人不要與第一人打此賭。
由此例我們一般的可定義如下之專有名詞。
我們再舉一個有關戰爭策略的例子如下:
例 3: A 軍對敵方 B 軍之軍事基地派出轟炸機 I 及 II。轟炸機 I 先飛行,然後 II 接著飛行。設 2 架轟炸機中有 1 架裝載炸彈,另一架護航,在出航前那架擔任之職務不明(為了機密),當然,敵方之軍事基地以一架戰鬥機迎擊該二轟炸機。在轟炸機上分別裝有速射砲。當戰鬥機攻擊後續之轟炸機 II 時,僅會遭遇轟炸機 II 之砲火。若戰鬥機攻擊先頭之轟炸機 I 時將遭遇二架轟炸機之砲火,因此,在前者戰鬥機被擊落之機率設為 0.3,後者之場合(受二架轟炸機之砲火攻擊),戰鬥機被擊落之機率 0.7。
當戰鬥機可躲避轟炸機之砲火峙,則戰鬥機可能擊落轟炸機之機率為 0.6。在轟炸機之立場者要到達目標將炮彈擲下,而戰鬥機方面,則欲阻止轟炸機達成目的,今欲問雙方之最適戰略(或策略)為何?亦即
下面我們來解此問題,先求此二人零和賽局。
下列考慮賽局之償付矩陣,即求其平均利得。
故償付矩陣為如下(表 3)
己方之策略為 A={a1,a2},敵方之策略為 B={b1,b2},償付矩陣
故 又 故 即 故此例無法在單純策略,即 A,B 中之戰略找到答案,必須將策略(或戰略)之範圍擴大才可獲得解,設在 A 上之機率之集合設為 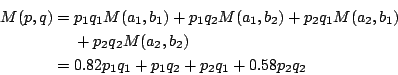
我們可得新的二人零和賽局 (E,H,M),而此賽局稱為原賽局 (A,B,M) 局之混合延伸 (mixed extension)。 此例在賽局 (A,B,M) 中無法得解,故我們考慮其混合延伸 (E,H,M) 之解。欲解此賽局我們先作一些準備,由此例我們可一般定義如下之專有名詞。
我們現在利用定理 1 解例 3 之賽局,因
M(p,q) = 0.82p1q1 + p2q2 + p2q1 + 0.58p2q2,
故
故由定理 1,
![\begin{eqnarray*}
\min_{q\in H}M(p,q)&=&\min_{j=1,2}M(p,b_j) = \min[M(p,b_1),M(p,b_2)] \\
&=&\min(1-0.18p_1,0.58+0.42p_1)
\end{eqnarray*}](img57.gif)
由圖 1 得知,
同樣, ![\begin{eqnarray*}
\max_{p\in E}M(p,q) &=& \max_{i=1,2}M(a_i,q)=\max[M(a_1,q),M(a_2,q)] \\
&=& \max[1-0.18q_1,0.58+0.42q_1]
\end{eqnarray*}](img59.gif)
可得 故 即賽局有解,己方之最佳混合戰略為 p*=(0.7,0.3),以機率 0.7 採用戰略 a1 並且以機率 0.3 採用戰略 a2,敵方之最佳戰略為 q*=(0.7,0.3),以機率 0.7 採用戰略 b1 並且以機率 0.3 採用戰略 b2。
己方如何實際實施最佳混合戰略 p*=(0.7,0.3),這可如下實施;先作 10 張大小厚度一樣之卡片,其中 7 張記 a1 其餘 3 張記 a2,將這些放入袋中混合後抽出一張,若 a1 則採用戰略 a1,即轟炸機 I 裝載炮彈,若抽出一張結果為 a2 時採用戰略 a2,即轟炸機 II 裝載炮彈。敵方亦可同樣實施,這一種遊戲同學間可以模擬試試,將可發見其中的樂趣。
為解例題 1,再證明下列定理 2。
利用此定理可如下解例 1,今第 2 人欲取策略
q=(q1,q2,q3) 使得 M(x,y)=k(定數),即解下列方程組(由表 1)。
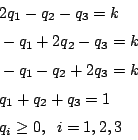
解之可得 k=0, 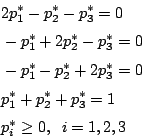
其解為
上述解法並非萬靈丹,有些需利用線性計劃法才可解出。
|
對外搜尋關鍵字: .賽局理論 .Von Neumann |
|
|
|
|
(若有指正、疑問……,可以在此 留言 或 寫信 給我們。) |
|
|
|
EpisteMath (c) 2000 中央研究院數學所、台大數學系 各網頁文章內容之著作權為原著作人所有 |
| 編輯:李渭天 | 最後修改日期:4/26/2002 |