從實數到複數

首頁 | 搜尋

．原載於數學傳播第一卷第一期
．作者當時任教於台大數學系

‧註釋

從實數到複數

繆龍驥

連結實數域中兩個真理的最短路徑是通過複數域

Jacques Hadamard

複數體 C 是實數體 R 的擴大，並且可以看成 R 上的一個二維向量空間。1 及 i（i²=-1）形成 C 的一組正交基底，每個複數 $c \in \mathbf{C}$ 都可以唯一地表成 1 及 i 的線性組合

$\begin{displaymath}c=a \cdot 1+ b \cdot i = a+bi, \qquad a,b \in \mathbf{R}\end{displaymath}$

根據這樣的觀點，我們現在提出下列兩個問題：

: 1. 如果一個數體 ^編者註 K 也是實數體 R 的一個擴大，並且可以看成 R 上的一個二維向量空間，則 K 與 C 的關係如何？
: 2. 對於任意大於 1 的自然數 n，是否存在一個數體 F，是 R 的一個擴大，並且可以看成 R 上的一個 n 維向量空間？

對於第一個問題，我們要證明 K 與 C 有相同的結構，即在 K 中可以找出一個元素 v₀，滿足

$\begin{displaymath}v^2_0 =-1, \eqno(1)\end{displaymath}$

以及對於每個元素 $u \in \mathbf{K}$ ，都可以唯一地寫成 1 與 v₀ 的線性組合：

$\begin{displaymath}u=a+bv_0, \qquad a,b \in \mathbf{R} \eqno(2)\end{displaymath}$

設 1 及 v 是 K 的一組任意的基底。則 $v^2 \in \mathbf{K}$ 也可以寫成 1 及 v 的線性組合：

$\begin{displaymath}v^2=r+sv, \qquad r,s \in \mathbf{R} \eqno(3)\end{displaymath}$

我們要由基底 1 及 v 作出一組新的基底 1 及 v₀，來滿足上面的要求(1)及(2)。

如果(3)式中 s=0，則取

$\begin{displaymath}v_0 = \frac{1}{\sqrt{\vert r\vert}} v,\end{displaymath}$

於是

$\begin{displaymath}v^2_0 = \frac{v^2}{\vert r\vert} = \frac{r}{\vert r\vert} = \pm 1.\end{displaymath}$

如果 $s \neq 0$ ，則先取

$\begin{displaymath}v' = 1-\frac{2}{s}v,\end{displaymath}$

顯然 $v' \neq 0$ ，而且 1 及 v' 是線性無關的。由(3)式得

$\begin{displaymath}v'^2 = (1- \frac{2}{s}v)^2 =1+4 \frac{r}{s^2} \neq 0.\end{displaymath}$

再令

$\begin{displaymath} v_0 = \frac{1}{\sqrt{\vert 1 + 4 \frac{r}{s^2}\vert}} v', \end{displaymath}$

同樣也得到 $v_0^2 = \pm 1$ 。

現在證明 v₀² = 1 不可能發生，因為否則的話，由 v₀² -1 = 0 即得 (v₀-1) (v₀+1) = 0。由於 v₀ 與 1 是線性無關的，所以

$v_0-1 \neq 0$ 及 $v_0 +1 \neq 0$ 。

但是在一個數體中，兩個不等於 0 的元素的乘積也不能等於 0。因此我們推得 v₀²=-1。

對於第二個問題，我們要證明，只有 n=2 時，才能作出一個實數體 R 的擴大 F，可以看成 R 上的 n 維向量空間。

假設對於一個大於 1 的自然數 n，存在一個這樣的數體 F，則必定 n=2。證明如下：

設 $v \in \mathbf{F}$ 但 $v \not\in \mathbf{R}$ ，n+1 個元素 v⁰ =1 , v¹=v , v² , $\cdots, v^n$ 在 n 維向量空間 F 中必定是線性相關的，因此存在一個實係數多項式：

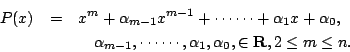
$\begin{eqnarray*} P(x) & = & x^m+\alpha_{m-1}x^{m-1}+ \cdots\cdots +\alpha_1 x+\... ...dots\cdots ,\alpha_1 ,\alpha_0, \in \mathbf{R}, 2 \leq m \leq n. \end{eqnarray*}$

使得 P(v)=0。一個 n 次實係數多項式在 R 上都可以分解成一次及二次的因式：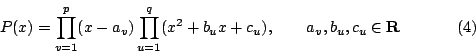

$\begin{displaymath} P(x)=\prod^p_{v=1}(x-a_v)\prod^q_{u=1}(x^2 + b_u x + c_u), \qquad a_v,b_u,c_u \in \mathbf{R} \eqno{(4)} \end{displaymath}$

由於在一個數體中一個乘積等於 0 時，其中至少有一個因子等於 0，所以在(4)式中至少有一個二次因式

$\begin{displaymath} Q(x)=x^2+bx+c, \qquad b,c \in \mathbf{R}, \eqno(5) \end{displaymath}$

使得 Q(v)=0，並且其中 $c \neq 0$ 。設 K 是由 1 及 v 在 R 上所產生 F 的一個二維子空間，由(5)式得到

v² = -bv-c

利用上式可以計算 K 中任意二元素 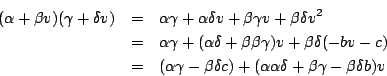$\alpha + \beta v$ 及 $\gamma + \delta v$ 的乘積：

$\begin{eqnarray*} (\alpha +\beta v)(\gamma +\delta v)&=&\alpha\gamma +\alpha\del... ...\beta\delta c)+(\alpha\alpha\delta +\beta\gamma -\beta\delta b)v \end{eqnarray*}$

上式右邊是 1 及 v 的線性組合，仍在 K 中。由此可知 K 中任意二元素的乘積仍屬於 K ，因此 K 本身就形成一個數體。根據第一個問題中討論的結果，K 與 C 有相同的結構，自然一般實係數二次方程式在 K 中也都有解。

如果 $w \in \mathbf{F}$ 是一個任意元素，則由上段中對 v 的討論可知，w 也是一個實係數二次方程式的解，所以 w 必屬於 K。由於 w 是 F 中一個任意元素，於是我們推得 F = K ，這也就是說，我們必定有 n=2。

基於以上討論的結果，我們可以說複數體 C 是 R 唯一的有限維擴大數體。

參考資料
Diederich-Remmert: Funktionentheorie I. Springer-Verlag 1972.

對外搜尋關鍵字：
．實數
．複數


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：康明軒 ∕ 校對：鄧惠文

最後修改日期：4/26/2002