| |
【例題】:
- (1)
- 光的反射定律與極小性:光的反射定律是
「入射線、反射線和平面在反射點的法線三線共面,而且兩者和法線的夾角相等。」
上述定律的幾何意義乃是光反射之途徑是在所有下述通路
之中取極小值。如 [圖1-23] 所示,
[ 圖1-23 ]
- (2)
- 給定
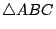 ,如[圖1-24(i)]所示令 ,如[圖1-24(i)]所示令 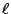 為 C
點外角的分角線。設 P 是 為 C
點外角的分角線。設 P 是 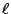 上一點, 上一點,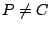 ,則恆有 ,則恆有
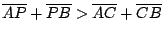 。 。
[ 圖1-24 ]
如 [圖1-24(ii)] 所示,令 B* 為 B 相對于 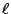 的反射對稱點,所以即有 的反射對稱點,所以即有
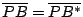 。由此可見, 。由此可見,
- (3)
- 內切圓作圖:對于一個給定的
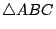 ,
唯一存在一個和其三邊相切的圓,稱之為 ,
唯一存在一個和其三邊相切的圓,稱之為
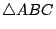 的內切圓(如 [圖1-25] 所示)。其作圖法如下:
的內切圓(如 [圖1-25] 所示)。其作圖法如下:
用 [基本作圖1.1],分別作 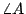 和 和 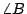 的角平分線。
則兩線的交點 O' 乃是具有和三邊等距的唯一之點,所以它就是所求作的內心
(內切圓圓心)。 的角平分線。
則兩線的交點 O' 乃是具有和三邊等距的唯一之點,所以它就是所求作的內心
(內切圓圓心)。
[ 圖1-25 ]
- (4)
- 設
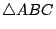 和 和
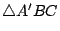 具有相同的外接圓,則
具有相同的外接圓,則
証明:如 [圖1-26] 所示,
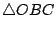 , ,
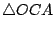 , ,
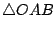 皆為等腰,所以其底角各別相等,即 [圖1-26] 所示之
皆為等腰,所以其底角各別相等,即 [圖1-26] 所示之
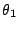 , , 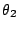 , , 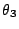 。再者, 。再者,
由此可見,上式之角度只和
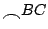 的大小有關,而和
的大小有關,而和
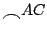 , ,
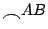 的大小無關。
的大小無關。
[注意:上式中的 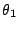 , , 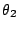 , , 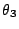 乃是有向角。如在 A''
的情形, 乃是有向角。如在 A''
的情形,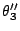 是負向角。] 是負向角。]
[ 圖1-26 ]
【習題】:
- (1)
- 鏡子成象的幾何原理:令 P' 是 P
對于
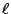 的反射對稱點。試証起始于
P 點的反射線的延長線共交于 P' 點(如 [圖1-27] 所示)。 的反射對稱點。試証起始于
P 點的反射線的延長線共交于 P' 點(如 [圖1-27] 所示)。
[ 圖1-27 ]
- (2)
- 試証明在[定理 1.10]中的「大角對大邊」部分。
- (3)
- 試証明在[基本作圖題 1.4]中的 X1X2 乃是過
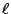 上 M 點的垂線。 上 M 點的垂線。
- (4)
- 試証明在[基本作圖題 1.5]中的 PP' 乃是垂直于
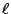 的直線。 的直線。
- (5)
- 設直線
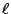 和圓 Γ 僅交于一點 P,試証 和圓 Γ 僅交于一點 P,試証
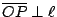 。 。
- (6)
- 過圓 Γ 上一點 P 作其切線
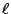 。 。
- (7)
- 設四邊形
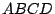 的兩對對邊各別等長,試証: 的兩對對邊各別等長,試証:
- (i)
- 其對角線互相平分;
- (ii)
- 其兩對對角各別相等。
- (8)
- 設四邊形
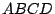 的兩對角線互相平分,試証: 的兩對角線互相平分,試証:
- (i)
- 其兩對對邊各別等長;
- (ii)
- 其兩對對角各別相等。
- (9)
- 設
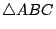 的 的 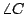 分角線等分對邊 分角線等分對邊
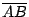 ,試証 ,試証
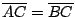 。
[延長 。
[延長 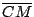 到 到
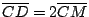 (如 [圖1-28] 所示),則可運用習題 (8) 之結果。]
(如 [圖1-28] 所示),則可運用習題 (8) 之結果。]
[ 圖1-28 ]
- (10)
- 給定
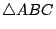 ,如[圖1-29]所示令 ,如[圖1-29]所示令 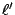 為 為 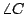 的分角線,P' 是
的分角線,P' 是 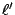 上一點, 上一點,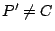 ,試証明 ,試証明
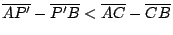 。 。
[ 圖1-29 ]
|
|
|