經濟學應用：最大淨利

翁秉仁

．作者任教於台大數學系
．本文節錄改寫自作者《微積分講義》

廠商（供給者）與消費者（需求者）構成經濟市場中的兩大要素。廠商投入資本（成本），製造商品，以市場調節的價格售予消費者，賺取利潤。作為理想中自私又理性的經濟人，廠商會盡量以取得最大的利潤為目標，這是非常自然的極值問題，微積分在此提供了基本的分析工具。倒是所謂的「最大利益」是什麼？這個問題，見仁見智，不在數學範疇中。

(1) 讓我們舉一個例子, 設有一獨佔市場的廠商, 其成本函數 C(x) 為:

$\begin{displaymath}C(x)=\frac{x^3}{10000}-\frac{3}{20}x^2+ 175 x + 50000 \end{displaymath}$

其中 x 是產品數, 成本則以元為單位. 為什麼成本函數呈現如後圖的模樣呢? 首先, C(0)>0, 表示在尚未生產時, 廠商必然已經先投資建造廠房; 其次, 在剛生產時, 成本相對於產量, 增加的「速度」(C'(x), 所謂的邊際成本, 見前面章節)很快; 必須等到產量足夠大後, 邊際成本才會降到最低點, 這是因為工廠有一個大致的生產規模, 在這個規模中, 才能最有效率的生產商品(稱為規模經濟 (economy of scale)); 也因此, 當產量高到一定地步後(超過規模負荷), 成本與邊際成本會再度快速增加, 廠商也許得雇用更多工人, 或者擴建新廠等.

習題：單從成本而言,就有兩種最小成本的概念：

: (a) 邊際成本最小, 此時每增加一單位成本, 可以增加最多單位的產量.
: (b) 平均成本最小：這時平均每單位成本的產量最大.

利用本例 C(x) 討論 (a), (b) 極值各自發生的位置, 並可與上一例作比較.

: 習題：說明平均成本的極小發生時,產量對成本的彈性等於 1.

(2) 由於假設廠商獨佔了市場，因此原則上（短期內）價格是由──廠商的產量（供）與消費者的需求（需）──所決定。由經濟學的供需定律知道，供應越充分，價格越低。設價格與供應量 x 的關係為：

$\begin{displaymath}P(x)=400 - \frac{x}{5}, \quad 0 \leq x \leq 2000 \end{displaymath}$

則廠商的收益函數為：

$\begin{displaymath}R(x)=x\cdot P(x)= x \cdot (400 - \frac{x}{5})\end{displaymath}$

: 習題：如果不計成本, 請問何時收益最大? (Ans.x=1000)

(3) 由於成本隨著多產而迅速增高, 相反地, 收益卻因多產而減少, 因此, 很顯然廠商的淨利

W(x)=R(x)-C(x)

一定會有最大值. 現考慮候選點 x=x₀,則

$\begin{displaymath}W'(x_0)=0 \;\;\Longleftrightarrow \;\;R'(x_0)=C'(x_0) \end{displaymath}$

在數理經濟學中, 這是一個基本的定律，

「廠商淨利的最大值發生在邊際收益等於邊際成本時.」

就本題而言, W(x)=R(x)-C(x)=

$\begin{displaymath}-\frac{x^3}{10000}-\frac{1}{20}x^2+225x-50000\end{displaymath}$

解 W'(x₀)= 0 求

$\begin{eqnarray*} x_0&=& 1000 (\frac{-1 \pm 2 \sqrt{7}}{6}) \mbox{({\McQ\char 1... ...kip 0.0pt plus0.2pt minus0.1pt{\MaQ\char 175})}\\ &\approx& 715 \end{eqnarray*}$

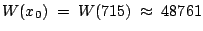且 $W(x_0) \;=\; W(715)\;\approx\; 48761$ .

(4) 淨利的極大值, 看起來是最理所當然的最大利益, 但是有沒有其他的可能性呢? 例如: 考慮廠商的平均淨利: 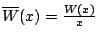$\overline{W}(x)=\frac{W(x)}{x}$ , 設其極大值發生在 x=x₁, 則

$\begin{displaymath}0=\overline{W}'(x_1)=\frac{W'(x_1)\cdot x_1-W(x_1)}{x_1^2} \end{displaymath}$

即

$\begin{displaymath}W'(x_1)=\frac{W(x_1)}{x_1}\end{displaymath}$

「平均淨利的極值發生在邊際淨利 = 平均淨利時.」

在本題中解得(要用到牛頓勘根法)

$\begin{displaymath}\overline{W}'(x_1)=0 \;\Rightarrow\; x_1 \approx 557 \end{displaymath}$

就總淨利而言:

$\begin{displaymath}W(557) \approx 42532 < W(715) \approx 48761 \end{displaymath}$

但以平均淨利來說, 則

$\begin{displaymath}\overline{W}(557)= 76.4 > \overline{W}(715) \approx 68.2 \end{displaymath}$

在 x=x₁ 時, 每單位產品所獲得的淨利最大. 讀者注意到 x₁<x₀, 在 x=x₀ 時雖然總淨利最大, 但是平均淨利卻小於 x=x₁, 這是不是一種浪費呢?

(5) 另外一個合理的考慮是: 淨利與付出成本之比較. 令

$\begin{displaymath}\widetilde{W}(x)=\frac{W(x)}{C(x)}=\frac{R(x)}{C(x)}-1 \end{displaymath}$

這表示每單位成本所獲得的淨利. 設其極值發生在 x=x₂, 則

$\begin{displaymath} \widetilde{W}'(x_2)=\frac{R'(x_2)C(x_2)-R(x_2)C'(x_2)}{C^2(x_2)}=0\end{displaymath}$

即

$\begin{displaymath}\frac{R'(x_2)}{R(x_2)} = \frac{C'(x_2)}{C(x_2)}\end{displaymath}$

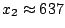經計算得 $x_2 \approx 637$ . 茲整理列表如下

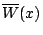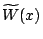	W(x) 淨利	$\overline{W}(x)$ 平均淨利	$\widetilde{W}(x)$ 淨利/成本
x₀=715	48761	68.2	0.361
x₁=557	42532	76.4	0.360
x₂=637	47189	74.1	0.373

在x=x₂ 時每單位投資的成本, 可以賺取最大的淨利, 廠商也可以很合理地說, 這才是他要尋找的最大利益, 因為這時錢是真正的花在刀口上, 其他的選擇, 毋寧是一種浪費, 倒不如將錢轉投資在其他產業上.

問題: 這裡的微積分是簡單的, 但各種說法, 到底哪一種才是正確的呢?

習題：某莊園中種植稻米, 其產量 F(x) 與投入耕作之農民人數 x 的關係如下:

$\begin{displaymath}F(x)= - \frac{x^3}{1000}+ \frac{3}{10} x^2 \end{displaymath}$

又假設市場上稻米單位價格 = 10 元

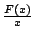: (1) 辨認下邊兩圖中, F(x), F'(x)(邊際產量) , $\frac{F(x)}{x}$ (平均產量)的曲線.
: (2) 您可以「經濟」地解釋 F(x) 的模樣嗎？為什麼三條曲線最後都呈遞減呢？ (稱為報酬遞減律)
: (3) 如果您是莊園的封建主人, 可不花成本的使喚農奴為您工作, 請問您該如何計算最大收益？
: (4) 如果您只是地主, 必須以固定的薪資 150 元/人雇用農工, 請模仿本節最後一例 (3), (4), (5), 討論如何計算最大收益？

習題：

某中盤商甲從大盤購進商品, 再轉賣給零售商, 為了保證貨源充裕, 遂租用倉庫儲備商品, 假設此商品的需求非常穩定為每天 100 單位, 因此甲的最佳經營策略, 在於謀求全年倉儲與轉運訂購成本之最小值。其成本可粗分為三類

(a) 每次訂購一整批商品手續費 1000 元.

(b) 運送商品每單位成本 10 元.

(1) 說明一次訂購之成本為

$\begin{eqnarray*} C(x)&=&1000+10x+\frac{1}{2}x(\frac{x}{100})\cdot (0.2)\\ &=&1000+10x+\frac{x^2}{1000} \end{eqnarray*}$

(2) 討論為什麼要極小化的函數是平均成本 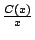$\frac{C(x)}{x}$ , 而不是 C(x)？

(3) 甲一次應訂購多少單位的商品？

(4) 如果訂購手續費為 α元/次, 運送成本為 β元/單位, 倉儲成本為 γ元/單位×天, 求極小值發生位置的公式？這公式與 β 有關嗎？解釋它.

對外搜尋關鍵字：
．牛頓勘根法

（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

最後修改日期：9/30/2001