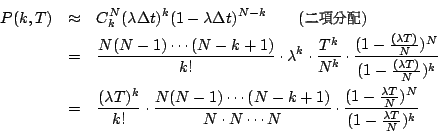Poisson 分配、指數分配與排隊理論

翁秉仁

．作者任教於台大數學系
．本文節錄改寫自作者《微積分講義》

Poisson 分配

考慮下列現象：每小時服務台訪客的人數，每天家中電話的通數，一本書中每頁的錯字數，某條道路上每月發生車禍的次數，生產線上的疵品數，學生到辦公室找老師的次數……。大致上都有一些共同的特徵：在某時間區段內，平均會發生若干次「事件」，但是有時候很少，有時又異常地多，因此事件發生的次數是一個隨機變數，它所對應的機率函數稱為 Poisson 分配。

一個 Poisson 過程有三個基本特性：

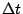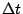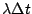: (1) 在一個短時間區間 $\Delta t$ 內，發生一次事件的機率與 $\Delta t$ 成正比： $\lambda \Delta t$ 。
: (2) 在短時間內發生兩次以上的機率可以忽略。
: (3) 在不重疊的時間段落裡，事件各自發生的次數是獨立的。

各位可以驗證上述各種實際的例子，是不是相當符合 Poisson 過程的定義？

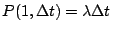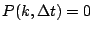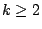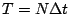現令 P(k,T) 表示在時間區間 T 中發生 k 次事件的機率（注意 T 表示時間區間的長度，而不是絕對時間），由(1)(2)知 $P(1,\Delta t)=\lambda\Delta t$ ，且 $P(k,\Delta t)=0$ , $k\geq 2$ 。現將 T 分割成 N 個短時間區段（即 $T=N\Delta t$ ），利用 (3) 各時間區段出現之事件是獨立的條件，可知

$\begin{eqnarray*} P(k,T)& \approx & C^N_k (\lambda \Delta t)^k(1-\lambda\Delta ... ...cdot \frac{(1-\frac{\lambda T}{N})^N}{(1-\frac{\lambda T}{N})^k} \end{eqnarray*}$

固定 k，當 $N\rightarrow\infty$ 時

$\begin{displaymath}P(k,T)=\frac{(\lambda T)^k}{k!}e^{-(\lambda T)} \quad (\mbox{... ...{\MbQ\char 41}} (1+\frac{\alpha}{N})^N\rightarrow e^{\alpha }) \end{displaymath}$

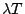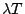由上可知 Poisson 分配是二項分配 B(N,p,q) 的一種極限，其中 Np= 常數 $\lambda T$ ，再讓 $N\rightarrow\infty$ 。另外，我們通常將 $\lambda T$ 記為 m，表示在時間區間 T 中，平均的發生次數（見下面習題）。

習題：
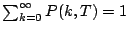: (1) 驗證 $\sum_{k=0}^{\infty} P(k,T)=1$ 。
: (2) 令 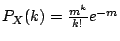$P_X(k)=\frac{m^k}{k!}e^{-m}$ , $k=1,2,3,\cdots$ 。求 E(X) 與 Var(X)。
(Ans. m, m.)

例.

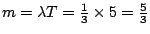一公司之電話通數大約每小時 20 通，求在 5 分鐘內一通電話也沒有的機率？每小時 20 通, 表示每分鐘平均 $\lambda =\frac{1}{3}$ 通/分。因此在 5 分鐘的時間區間中, 平均的電話通數為 $m=\lambda T= \frac{1}{3}\times 5=\frac{5}{3}$ 。所以

$\begin{displaymath}P(k)\;\equiv\;P(k,5)\;=\;\frac{(\frac{5}{3})^k}{k!} e^{-\frac{5}{3}}, \quad k=0,1,2,\cdots\end{displaymath}$

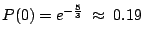所以沒有一通電話的機率 $P(0)= e^{-\frac{5}{3}}\;\approx\; 0.19$ 。有了 P(k)，我們可以回答許多類似的問題：在 5 分鐘內有 4 通電話的機率是 $P(4)=\frac{\frac{5}{3}^4}{4!}e^{-\frac{5}{3}}\approx 0. 06$ ，大概每十六次才有一次。在 5 分鐘內有超過 3 通電話的機率是

$\begin{displaymath}\sum_{k=4}^{\infty}\frac{(\frac{5}{3})^k}{k!} e^{-\frac{5}{3}... ...=0}^{3}\frac{(\frac{5}{3})^k}{k!} e^{-\frac{5}{3}}\approx 0.09\end{displaymath}$

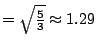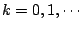經計算這個機率分配的期望值 $= \frac{5}{3}$ ，標準差 $=\sqrt{\frac{5}{3}}\approx 1.29$ 。右圖是 P(k) 的圖形，當然由於 $k= 0,1,\cdots$ ，所以這只是部分圖形。讀者可與一般的二項分配的圖形比較。

$E(X)=\frac{5}{3} \approx 1.67 \;\sqrt{Var(X)}=\sqrt{\frac{5}{3}} \approx 1.29$

例. 下表是 1910 年 Rutherford 觀察放射性物質放射 α 粒子的記錄，每次觀察 7.5秒，共觀察 2608 次。

粒子數	次數	頻率	P(k)
0	57	0.022	0.021
1	203	0.078	0.081
2	383	0.147	0.156
3	525	0.201	0.201
4	532	0.204	0.195
5	408	0.156	0.151
6	273	0.105	0.097
7	139	0.053	0.054
8	45	0.017	0.026
9	27	0.010	0.011
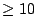$\geq 10$	16	0.006	0.007
$m=\frac{10094}{2608}=3.87$

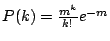這裡 P(k)=P(k,7.5)，其中 $P(k)= \frac{m^k}{k!}e^{-m}$ ，m=3.87（見表最末欄），為 7.5 秒中 α 粒子放射之平均個數。可以看到，如果假設 α 粒子的放射是一 Poisson 過程，結果相當吻合。

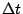例. 令一放射性物質在時間 t 時所含之放射性粒子總量為 N(t)，如果假設放射粒子是一 Poisson 過程，則在短時間 $\Delta t$ 後，

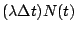$\begin{displaymath}N(t+\Delta t)-N(t)=-(\lambda \Delta t)N(t) \end{displaymath}$

注意到 $(\lambda\Delta t)N(t)$ 是一期望值的形式。所以

$\begin{displaymath}N'(t)\approx \frac{N(t+\Delta t)-N(t)}{\Delta t}=-\lambda N(t) \end{displaymath}$

這可看成輻射定律的「證明」。

對外搜尋關鍵字：
．輻射定律

指數分配與排隊理論

令 W 表示在 Poisson 過程中，由開始到第一次事件發生的時間（這是一隨機變數）。由上節知

$\begin{eqnarray*} P(W>t)&=&P( \mbox{{\MaQ\char 202}} [0,t] \mbox{{\MaQ\char 50... ...t minus0.1pt{\MbQ\char 222}} ) \\ &=&e^{-\lambda t}, \quad t>0 \end{eqnarray*}$

但

$\begin{displaymath}F_W(t)=P(W\leq t)=1-P(W>t) =1-e^{-\lambda t} \end{displaymath}$

所以

$\begin{displaymath}f_W(t)=F_W'(t)=\lambda e^{-\lambda t}, \quad t>0 \end{displaymath}$

這個機率分配稱為指數分配。可計算得 $E(W)=\frac{1}{\lambda}$ ，這就是第一次事件發生的平均時間。另外， $Var(W)=\frac{1}{\lambda^2}$ 。

現在讓我們討論排隊理論。排隊的現象無所不在：買各種票、吃自助餐、超商、百貨公司……等。顧客揣度「應該排那一服務櫃台會比較快？」「到底還要排多久？」是城市生活的基本問題；相對的，商家也要盤算到底在何時要開幾個窗口櫃台才符合成本，探討這個問題的數學理論通稱為排隊理論，而指數分配經常被用到排隊理論，當作服務客人時間（這是一隨機變數）的機率密度函數。

讓我們假設某櫃台，服務客人的平均時間為 μ，想像在服務結束後，櫃員會亮燈請下一位客人進來，則亮燈的平均時間是 μ。若將「燈亮」視為一事件發生，則亮燈的過程近似於一 Poisson 過程。而且前面定義的 W 正好表示兩次亮燈間的間隔。所以 W 的機率密度函數是指數分配：

$\begin{displaymath}f_W(t)=\frac{1}{\mu}e^{-\frac{1}{\mu}t},\quad t>0 \end{displaymath}$

例.

現假設一櫃台平均服務時間為 3 分鐘，設等待時間的機率密度函數為

$\begin{displaymath}f_W(t)=\frac{1}{3} e^{-\frac{t}{3}}, t>0 \end{displaymath}$

(1)等候時間超過6分鐘的機率是多少？

$\begin{eqnarray*} P(W>6)&=& \int_{6}^{\infty}{\frac{1}{3} e^{-\frac{t}{3}}}dt = ... ...\frac{t}{3}}\big)\big\vert _6^b \\ &=& e^{-2}\; \approx \; 0.14 \end{eqnarray*}$

事實上，等候超過 T 分鐘的機率是 $e^{-\frac{T}{3}}$ 。

(2) 另一個合理的問題是，如果在我前面還有另一個客人，則我怎麼描述，我等待時間的機率分配呢？

令 W₁ 是第一個客人等待的時間，W₂ 是第一個客人開始被服務後，我所等待的時間，則 $W_1 \;\sim\; W_2\; \sim \; W$ ，而且總等待時間 U = W₁+W₂，另外顯然 W₁ 與 W₂ 是互相獨立的。所以我們的問題就是要計算 f_U(t)，由309頁例子的方法，可以計算得

$\begin{displaymath}f_U(t) = \frac{1}{9} t e^{-\frac{t}{3}},\quad t>0 \end{displaymath}$

或者，如果將指數分配 f_W(t) 想成是 $\Gamma(1,\frac{1}{3})$ 分配，則此相當於

$\begin{displaymath}\Gamma(1,\frac{1}{3})+\Gamma(1,\frac{1}{3}) \;\sim\; \Gamma(2,\frac{1}{3})\qquad \end{displaymath}$

因此如果我們想知道總等候時間不超過 5 分鐘的機率，則

$\begin{eqnarray*} P(U\leq5)&=& \int_{0}^{5}{\frac{1}{9} t e^{-\frac{t}{3}}}dt ... ...0^5 + 3 \int_0^5 e^{-\frac{t}{3}} \; dt \right)\\ &\approx& 0.5 \end{eqnarray*}$

有一半的機會。

(3) 如果前面有 n-1 個客人時，則可定義 $U=W_1+W_2+ \cdots + W_n$ ，其中 W_i 彼此獨立，由 Gamma 分配性質知 $U \sim \Gamma(n, \frac{1}{3})$ ，即

$\begin{displaymath}f_U(t)\; =\; \frac{1}{3^n(n-1)!} t^{n-1}e^{-\frac{t}{3}}, \quad t>0 \end{displaymath}$

這告訴我們 $\Gamma(\alpha, \beta)$ 分配與排隊理論的關係。我們將細節留作習題。

習題：
: (1) 超級市場一服務員平均服務時間為 2 分鐘，若用指數分配當作等候時間之機率分配，則機率密度函數是什麼？
: (2) 如果他正開始服務一位客人，而你前面還有一位客人在等候，則你會等超過 6 分鐘的機率是多少？
: (3) 若服務員甲平均服務時間為 2 分鐘，而服務員乙之平均服務時間為 3 分鐘，如果你選擇乙，你朋友選擇甲，且一起開始接受服務，則你會比朋友快的機率是多少？（當然甲與乙的服務是相互獨立的）你能給出一個一般的計算公式嗎？

（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

最後修改日期：9/30/2001