費馬原理──光的路徑

費馬原理──光的路徑
Fermat Principle

翁秉仁

．作者任教於台大數學系
．本文節錄改寫自作者《微積分講義》

讓我們先考慮一個例子, 如果你在湖岸邊看到一個小孩溺水, 你希望用最快的速度去救他(當然假設您是游泳好手), 您該怎麼辦? 如下圖, 當然您絕不會選擇 (1) 的路線. 但是您也會放棄最短的直線 (2), 而改以 (3) 來取代, 為什麼?

因為您(該)知道, 人在路上跑步的速度遠比水中的速度來得快, 為了節省時間, 我們勢必要在陸上多跑些距離, 再跳到水裡去. 費瑪運用同樣的想法, 去描寫光學中光行進的路徑, 稱為費瑪原理:

「光所遵循的路徑是最節省時間的路徑.」

(而不是最短的路徑 !!)

而游泳救溺的故事, 在光學中就是折射現象的描述. 如右圖, 設光在介質 1 中的速度是 v₁, 在介質 2 中的速度是 v₂. 由 (0,a) 點出發到 (d,-b) 點, 請問光的路徑? 設光與介面相交點的座標為 (x,0), 則它所花費的時間是

$\begin{displaymath}t(x)=\frac{\sqrt{x^2+a^2}}{v_1}+\frac{\sqrt{(d-x)^2+b^2}}{v_2}\end{displaymath}$

$\begin{displaymath}t'(x)=\frac{x}{\sqrt{x^2+a^2}}\cdot \frac{1}{v_1}-\frac{(d-x)} {\sqrt {(d-x)^2+b^2}}\cdot \frac{1}{v_2}=0 \end{displaymath}$

但由下圖知,

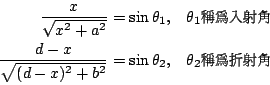
$\begin{eqnarray*} \frac{x}{\sqrt{x^2+a^2}}=\sin\theta_1, &\theta_1 \mbox{{\McQ\c... ...{\MeQ\char 166}\hskip 0.0pt plus0.2pt minus0.1pt{\McQ\char 105}} \end{eqnarray*}$

則由 t'(x)=0 (費瑪原理)得

$\begin{displaymath}\frac{\sin\theta_1}{\sin\theta_2}=\frac{v_1}{v_2} \end{displaymath}$

這稱為折射定律或Snell定律.(為什麼此時 t(x) 式最小值?)

: 習題：用費瑪原理說明反射定律:入射角= 反射角 .

（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

最後修改日期：9/30/2001