�Ϊä�
�D�@�̥��Щ�x�j�ƾǨt
�D����`����g�ۧ@�̡m�L�n�����q�n
|
�ǬV�f���X���ҫ�
�Ϊä� |
�D�@�̥��Щ�x�j�ƾǨt �D����`����g�ۧ@�̡m�L�n�����q�n |
|
���U�ڭ̭n�����A�b�ǬV�f���Ǽ��Ҧ����]�|�X�{ Logistic �ҫ��C���]���@�ضǬV�f�A��IJ�K�|�P�V�A�ӥB�P�V��K��K�̥ä��A�ǡA�]���b�ɶ� t�A�Y�������Ҧ��H�f M ���A�i�����w�P�V�H�f P(t) �P���P�V�H�f M-P(t)�A�]
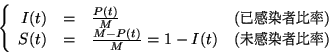
���۰��] �b �O�b���������A�C�H�C�ѥ�����IJ���H�ơA�h�f�H�]�P�V�̡^�C�Ѫ��W�[�v��
�C�ӯf�H�����C�ѱ�IJ�����d�̤�v �� �`�f�H�� ��
�ҥH�ϥγs��ҫ��A�N�o��
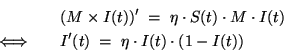
�o�O�@�� Logistic �ҫ��C
�g�� I(t) ���n�B�O�����u�����H�f�� M �����F�A��Ҫ��ܤƤ~�O���n���A�ҥH�ѫe�������R�A�ڭ̪��D�Ѧ��u I(t)�]���M 0<I(t)<1�^�O�@�� S �����u�A��
���G�o�����b�����ΤH�f�K���B�A�ѩ� �b �ȸ��j�A�ǬV�f�̱����X���{���֩�m���A�]�����������ó����b����̱��ɡA�ɶ����O��j�C
|
��~�j�M����r�G �DLogistic�ҫ� �D�����ȩw�z |
���M���O�Ҧ����ǬV�f����ä[�K�̡A�f�H�b�v¡��A���i��A���s�P�V�f���A�o�ɧڭ̻ݭn�ק�ҫ���
�䤤 �b �P�e�A�m ���ܨC��v¡���H�Ƥ�v�A�]�� �즡�i�H��g�� 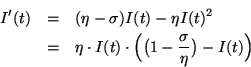
�o�]�O Logistic �ҫ��C�ߤ@���ҥ~�O
�o�̥X�{�@�ӭ��n�����СG��IJ�� �]�A�w�q��

�ӥB
�ڭ̨� �] �Ȥ����T�ر��p�ӰQ�סG
�]�����F�����̱��A���n���O�n�N �] �Ƚզ� <1�A��
�o�dz��P�`�ѧ����ŦX�C
�t�~�A�o�@��¡�ᤣ�|�A�P�V���ǬV�f�A�p�G�b�H�����|���w�g���v�y�[�A���q�`�P�H�������w�g�F���Y�إ��šA�o�دe�f���S�x�O���b�����y�檺�ϰ줺�J���|�P�R�]���|����]�o�N�O
|
|
�w���`�g
�b�e���Ҥl�������l�� x0 = 0.1 �ɡA�ڭ�ı�o�ܯ��աC���O�p�G�q�t�@�Ө��Q�A�]�\�ä������p���C�p�G�ڭ̯u��N x0 ����b
�o���O�w�����ت����n�ʡA�ѩ�̭]���`�g�A�@�ӵL��ܤO�����d�H�i�H�ಾ����K�̤O���v¡�̡A�b�j�W�Ҫ��̭]���ث�Ax0 �i�H�u���ܤp�A�]�����ı���ǬV�̱��������A�N�O�Q�ιw�����رN x0 ��C�챵IJ�ƪ��˼ƥH�U�]�Y���ı�IJ�� <1�^�C
�o�ӶǬV�f�ҫ��̦��쪺���G�A�O���F�����ǬV�f�̱��X���A�w�����بèS�����n����������ت��a�B�C�o���������䪺���D�A�O�n���D�ӶǬV�f�b���a�������ǤU����IJ�� �b�C�Ҧp�p��������IJ�Ƴq�`���ʤ�y�ӱo�p�A�z�פW�N����ʤ�y���������O�ӱo�j�]�ѦҲ��D�^�C���M�b��a�]�F���\�U�A�Y���ǬV�f���w�������٬O���H�������ؼСA�����̭]�������Q�ɡA�ӥB�S�O��IJ�ƧC���ǬV�f�ɡA�W�z���Ҽ{�N�|���ߡC���M�A�p�P�Ĥ@�`���Q�סA��IJ�ƨä��O�e�f���S�w�ʽ�A�P���a�������Ҥ]�߲߬����C�����åͤ��ǡA�W�i���Ĥ������k�A�����U���Y��w�����ت��W�ҡC �ڭ̤w�g�F�ѶǬV�f��IJ�ƪ����n�ʡA�U�������D�Q�צp���ڴx����IJ�ơC
|
|
|
|
|
|
EpisteMath (c) 2000 ������s�|�ƾǩҡB�x�j�ƾǨt �U�����峹���e���ۧ@�v����ۧ@�H�Ҧ� |
| �̫�ק����G9/30/2001 |