經濟學應用:合作還是不合作
翁秉仁
.作者任教於台大數學系
.本文節錄改寫自作者《微積分講義》
|
經濟學應用:合作還是不合作
翁秉仁 |
.作者任教於台大數學系 .本文節錄改寫自作者《微積分講義》 |
|
假設台灣只有兩地生產某種草藥,而兩地分別控制在兩個財團 X 與 Y 手裡,由於是天然產品,不需要任何成本,收益即是淨利。設控制市場價格的函數為
P(t)=100-t
考慮幾種競爭策略(設 X 之產量為 x 單位,Y 產量為 y 單位)
我們將 X,Y 合作與不合作(背叛)兩種策略列表如下
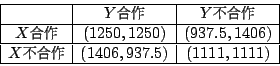
(a,b) 中 a 表示 X 方得到的利潤,b 表示 Y 得到的利潤。 注意到
這樣的策略利益配置在(非零和)對局論中稱為囚犯困境 (prisoner's dilemma) 1 ;是討論由自私理性的眾多個體,如何演化出利他合作的群體行為時一個非常典型的問題:生物的利他行為、人類道德的起源、社會組織的出現、政黨的協調、國家的合作競爭等,都與這個合作與背叛的母題習習相關。
|
|
|
|
|
|
EpisteMath (c) 2000 中央研究院數學所、台大數學系 各網頁文章內容之著作權為原著作人所有 |
| 最後修改日期:9/30/2001 |